Given v'=(1−v/c)vandv'=(1−v/c)v√1−v2/c2 For what value v/c, these question differ by 10%
Step by step video & image solution for Given v'=(1-v//c)vandv'=((1-v//c)v)/sqrt(1-v_(2)//c_(2)) For what value v/c, these question differ by 10% by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
If ∣∣→V1+→V2∣∣=∣∣→V1−→V2∣∣andV2 is finite, then
AV1 is parallel to V2B→V1=→V2CV1andV2 are mutually perpendicularD∣∣→V1∣∣=∣∣→V2∣∣The capacities of two parallel plate capacitors are C1 and C2 and their respective potential are V1 and V2. If they are connected by a thin wire, then
(A) Commen potential will be C1V1+C2V2C1+C2, if plates of same polarities are connected together
(B) Loss of energy will be 12C1C2C1+C2(V1−V2)2, if plates of same polarities are connected together
(C) Common potential will be |C1V1−C2V2|C1+C2, if plates of opposite polarities are connected togetherA(A),(B),(c)B(B),(c),(D)C(A),(B),(D)D(A),(B),(c),(D)A circuit shown in the figure consists of a battery of emf 10V and two capacitance C1 and C2 of capacitances 1.0μF and 2.0μF respectively. The potential difference VA−VB is 5V
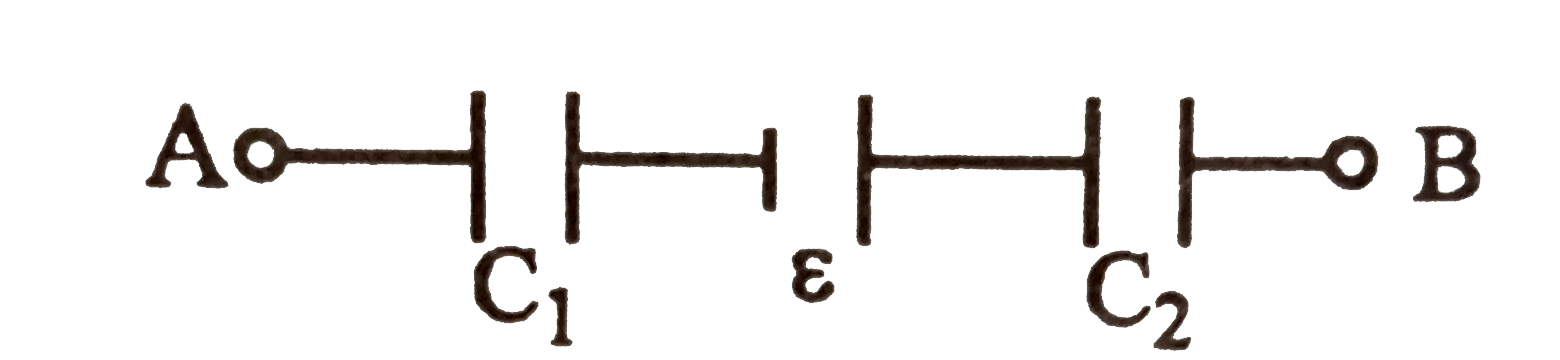 ACharge on capacitor C1 is equal to charge on capacitor C2BVoltage across capacitor C1 is 5V.CVoltage across capacitor C2 is 10VDEnegry stored in capacitor C1 is two times the enegry stored in capacitor C2.
ACharge on capacitor C1 is equal to charge on capacitor C2BVoltage across capacitor C1 is 5V.CVoltage across capacitor C2 is 10VDEnegry stored in capacitor C1 is two times the enegry stored in capacitor C2.
Given that Cp−CV=Randγ=Cp/CV, where Cp=Molar specific heat at constant pressure, CV=molar specific heat at constant volume. Then CV=
View Solution
When pressure is increases at constant temp volume of gas decreases AB→gases,BC→vpour+liquCD→liqu
critical point: At this point all the physical propeties of liquid phase will be same as the physical properties in vapour such as, density of liquid = density of vapour
Tc or critical temp: Temperature abive which a gas can not be liquified
Pc or critical pressure: minimum pressure which must be applied at critical temp to convert the gas into liqid.
Vc or critical volume: volume occupied by one mole of gas at Tc&Pc
CRITICAL CONSTANT USING VANDERWAAL EQUATIONS:
(P+aV2m)(Vm−gb)=RT==⇒(PV2m+a)(Vm−b)=RTV2mPV3m+aVm−PbV2m−ab−RTV2m=0==⇒V3m+V2m(b+RTP)+aPVm−abP=0
since equation is cubic in Vm hence there will be three roots of equation of any temperature and pressure. At critical point all three roots will coincide and will given single value of Vm=Vc at critical point. Vander Waal equation will be
V3m−V2m(b+RTCPC)+aPCVm−abPC=0...(i)
But at critical point all three roots of the equation should be equal, hence equation should be:
Vm=Vc
(Vm−Vc)3=0
V3m−3V2mVc+3VmV2c−V3c=0..(2)
comparing with equation (1)
b+RTcPc=3Vc ...(i) aPc=3V2c ...(ii) abPc=V3c ..(iii)
From (ii) and (iii), Vc=3b
From (ii) Pc=a3V2c substituting Pc=a3(3b)2=a27b2
From (i) RTcPc=3Vc−b=9b−b=8b⇒Tc=8a27Rb
At critical point, the slope of PV curve (slope of isotherm) will be zero at all other point slope will be negative zero is the maximum value of slope.
(∂P∂Vm)TC=0..(i)∂∂Vm(∂P∂Vm)TC=0...(ii)
{Mathematically such points an known as point of inflection (where first two derivatives becimes zero)}
using the two TcPc and Vc can be calculated by

A scientist proposed the following equation of state P=RTVm−BV2m+CV3m. If this equation leads to teh critical behaviour then critical temperature is:
View SolutionA monoatomic gas expands following as thermodynamic law P=C1V+C2, where C1,C2 are constants, from state A(V0,3P0) to B(3V0,P0).What will be the volume of the gas upto which it absorbs heat?
View SolutionGiven the , Cp−Cv=R and γ=CpVv where Cp=molar specific heat at constant pressure Cv=molar specific heat at constant volume. Then Cv=
View SolutionVelocity v is given by v=at2+bt+c, where t is time. What are the dimensions of a,bandc respectively?
View Solution