A diffraction grating used at normal incidence gives a line λ1=600Å in a certain order supermposed on another line λ2=450Å of the next higher order. If the angle of diffraction is 30∘ how many lines are there in 1 cm of the grating.
To solve the problem step by step, we will follow the reasoning provided in the video transcript.
Step 1: Convert Wavelengths to Centimeters
We are given two wavelengths:
- λ1=6000Å=6000×10−10m=6×10−5cm
- λ2=4500Å=4500×10−10m=4.5×10−5cm
Step 2: Identify the Angles
The angle of diffraction for both wavelengths is given as:
- θ1=θ2=30∘
Step 3: Calculate Sine of the Angles
Using the sine function:
- sin(30∘)=0.5
Step 4: Write the Diffraction Grating Equations
For the first wavelength λ1:
a+bsin(θ1)=nλ1(Equation 1)
For the second wavelength λ2:
a+bsin(θ2)=(n+1)λ2(Equation 2)
Step 5: Substitute Known Values
Substituting sin(30∘)=0.5 into the equations:
1. a+b(0.5)=n(6×10−5)
2. a+b(0.5)=(n+1)(4.5×10−5)
Step 6: Divide Equation 2 by Equation 1
By dividing the two equations:
n(6×10−5)(n+1)(4.5×10−5)=1
This simplifies to:
n(6)=(n+1)(4.5)
Step 7: Solve for n
Expanding and rearranging gives:
6n=4.5n+4.5⟹1.5n=4.5⟹n=3
Step 8: Calculate the Number of Lines per Centimeter
Using the formula for the number of lines N:
N=1a+b=sin(θ1)nλ1
Substituting the known values:
N=0.53×6×10−5=0.51.8×10−4=0.5×1041.8≈2777.78lines/cm
Final Answer
Thus, the number of lines in 1 cm of the grating is approximately 2778 lines/cm.
---
We are given two wavelengths:
- λ1=6000Å=6000×10−10m=6×10−5cm
- λ2=4500Å=4500×10−10m=4.5×10−5cm
The angle of diffraction for both wavelengths is given as:
- θ1=θ2=30∘
Using the sine function:
- sin(30∘)=0.5
For the first wavelength λ1:
a+bsin(θ1)=nλ1(Equation 1)
For the second wavelength λ2:
a+bsin(θ2)=(n+1)λ2(Equation 2)
Substituting sin(30∘)=0.5 into the equations:
1. a+b(0.5)=n(6×10−5)
2. a+b(0.5)=(n+1)(4.5×10−5)
By dividing the two equations:
n(6×10−5)(n+1)(4.5×10−5)=1
This simplifies to:
n(6)=(n+1)(4.5)
Expanding and rearranging gives:
6n=4.5n+4.5⟹1.5n=4.5⟹n=3
Using the formula for the number of lines N:
N=1a+b=sin(θ1)nλ1
Substituting the known values:
N=0.53×6×10−5=0.51.8×10−4=0.5×1041.8≈2777.78lines/cm
Thus, the number of lines in 1 cm of the grating is approximately 2778 lines/cm.
Topper's Solved these Questions
Similar Questions
The angle of diffraction of the second order maximum of wavelength 5×10−5 cm is 30∘ in the case of a plane transmission grating. How many lines are there in 1 cm of the grating surface.
View SolutionA plane transmissio grating when illuminated with normal light produces a second order diffraction at 30∘ for wavelength λ=500 Å. Calculate the number of lines per cm on the grating.
View Solution
Knowledge Check
A diffraction grating is ruled with 600 lines per millimetre. When monochromatic light falls normally on the grating, the first order diffracted beams are observed on the far side of the grating each making an angle of 15∘ with the normal to the grating.
What is the frequency of the light?A(a) 1.2×1013HzB(b) 4.7×1013HzC(c) 1.9×1014HzD(d) 7.0×1014HzIn a single slit diffraction pattern, the first minima for a wavelength λ1=6000 Å coincides with the first maxima for a wavelength λ2. Then the value of λ2 is
A8000 ÅB4000 ÅC5500 ÅD3500 ÅA 30mm wide diffraction grating produces a deviation of 30∘ in the second order principal maxima. The wavelength of light used is 600nm. The total number of slits in the grating is:
A(a) 12500B(b) 25000C(c) 11500D(d) 15000
A diffracting grating 1 cm wide has 1200 lines and is used in second order. What is the diffraction angle for light of wavelength 550 nm?
View SolutionA transparent diffraction grating has a period d=1.50μm. Find the angular disperison D (in angular minutes per nanometers) corresponding to the maximum of highest order for a spectral line of wavelength λ=530mm of light falling on the grating
(a) at right angles,
(b) at the angle θ0=45∘ to the normal.
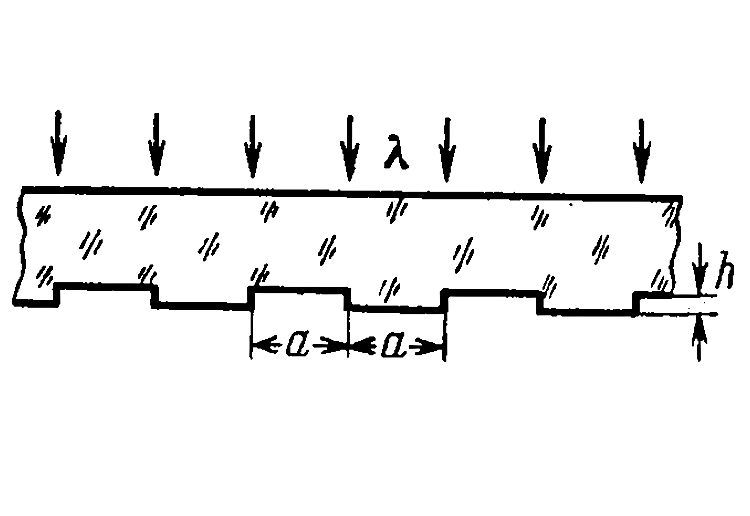
View SolutionA plane light wave with wavelength λ falls normally on a phase diffraction grating whose side view is shown in Fig. The grating is cut on a glass plate with refractive index n. Find the depth h of the lines at which the intensity of the central Fraunhofer maximum is equal to zero. what is in this case the diffraction angle corresponding to the first maximum?
View SolutionWith light falling normally on a transparent diffraction grating 10mm wide, it was found that the components of the yellow line of sodium (589.0 and 589.6nm) are resolved beginning with the fifth order of the spectrum. Evaluate:
(a) the period of this grating,
(b) what must be the width of the grating with the same period for a double λ=460.0nm whose components differ by 0.13nm to be resolved in the third order of the spectrum.
View SolutionHow many orders will be visible if the wavelength of the incident radiation is 5000 Å and the number of lines on the grating is 101319 per metre.
View Solution

