Two point charges of are placed m apart from each other. Calculate (i) electric field and electric potential at a distance of 0.6m from the dipole in broad-side-on position (ii) electric field and electric potential at the same point after rotating the dipole through .
To solve the problem, we need to calculate the electric field and electric potential at a distance of 0.6 m from a dipole consisting of two point charges of +3 µC each, first in a broad-side-on position and then after rotating the dipole through 90 degrees.
1. Calculate the Dipole Moment (P):
P=q⋅d=(3×10−6C)⋅(2×10−3m)=6×10−9C⋅m
2. Electric Field (E) at the Equatorial Line:
The formula for the electric field at a point on the equatorial line of a dipole is given by:
E=k⋅Pr3
where k=14πϵ0≈9×109N⋅m2/C2.
Substituting the values:
E=(9×109)⋅(6×10−9)(0.6)3
E=54×1000.216=250N/C
3. Electric Potential (V) at the Equatorial Line:
The electric potential at the equatorial line of a dipole is always zero:
V=0V
Part (ii): Electric Field and Electric Potential after Rotating the Dipole through 90 Degrees
1. Electric Field (E) on the Axis of the Dipole:
The formula for the electric field at a point on the axis of a dipole is given by:
E=2k⋅Pr3
Substituting the values:
E=2⋅(9×109)⋅(6×10−9)(0.6)3
E=108×1000.216=500N/C
2. Electric Potential (V) on the Axis of the Dipole:
The formula for the electric potential at a point on the axis of a dipole is given by:
V=k⋅Pr2
Substituting the values:
V=(9×109)⋅(6×10−9)(0.6)2
V=54×1000.36=150V
Final Results:
- Part (i):
- Electric Field E=250N/C
- Electric Potential V=0V
- Part (ii):
- Electric Field E=500N/C
- Electric Potential V=150V
P=q⋅d=(3×10−6C)⋅(2×10−3m)=6×10−9C⋅m
The formula for the electric field at a point on the equatorial line of a dipole is given by:
E=k⋅Pr3
where k=14πϵ0≈9×109N⋅m2/C2.
E=(9×109)⋅(6×10−9)(0.6)3
E=54×1000.216=250N/C
The electric potential at the equatorial line of a dipole is always zero:
V=0V
The formula for the electric field at a point on the axis of a dipole is given by:
E=2k⋅Pr3
Substituting the values:
E=2⋅(9×109)⋅(6×10−9)(0.6)3
E=108×1000.216=500N/C
The formula for the electric potential at a point on the axis of a dipole is given by:
V=k⋅Pr2
Substituting the values:
V=(9×109)⋅(6×10−9)(0.6)2
V=54×1000.36=150V
- Part (i):
- Electric Field E=250N/C
- Electric Potential V=0V
- Electric Field E=500N/C
- Electric Potential V=150V
Topper's Solved these Questions
- ELECTRIC POTENTIAL AND ELECTRIC FLUXBook:SL ARORAChapter:ELECTRIC POTENTIAL AND ELECTRIC FLUXExercise:Problem
Explore 15 Videos
- ELECTRIC POTENTIAL AND ELECTRIC FLUXBook:SL ARORAChapter:ELECTRIC POTENTIAL AND ELECTRIC FLUXExercise:Problems for self practive
Explore 61 Videos
- CURRENT ELECTRICITYBook:SL ARORAChapter:CURRENT ELECTRICITYExercise:Problems For Self
Explore 101 Videos
- ELECTRICAL INSTRUMENTSBook:SL ARORAChapter:ELECTRICAL INSTRUMENTSExercise:Problem for self practice
Explore 81 Videos
Similar Questions
Two charges +0.2μμCand−0.2μμC are placed 10−6cm apart. Calculate electric field at an axial point at a distance of 10 cm from their middle point.
View SolutionTwo charges +30μCand−30μC are placed 1cm apart. Calculate electric field at a point on the axial line at a distance of 20cm from the centre of dipole.
View Solution
Knowledge Check
The electric field of an electric dipole at a point on its axis , at a distance d from the center of the dipole, varies as
A1dB1d2C1d3D1d32An electric dipole is placed in an electric field generated by a point charge
AThe net electric force on the dipole must be zeroBThe net electric force on the dipole may be zeroCThe torque on the dipole due to the field must be zeroDThe torque on the dipole due to the field may be zero
Two charges +20μCand−20μC are held 1cm apart. Calculate the electric field at a point on the equatorial line at a distance of 50cm from the center of the dipole.
View SolutionThe electric field at a point at a distance r from an electric dipole is proportional to ......
View SolutionAn electric dipole is placed in an electric field generated by a point charge then
View SolutionAn electric dipole is placed in an electric field generated by a point charge then
View SolutionTwo charges, each of 5μC but opposite in sign, are placed 4 cm apart. Calculate the electric field intensity of a point that is a distance 4 cm from the mid point on the axial line of the dipole.
View SolutionTwo short dipoles are placed perpendicularly as shown. Find electric field and potential at charge distance r.
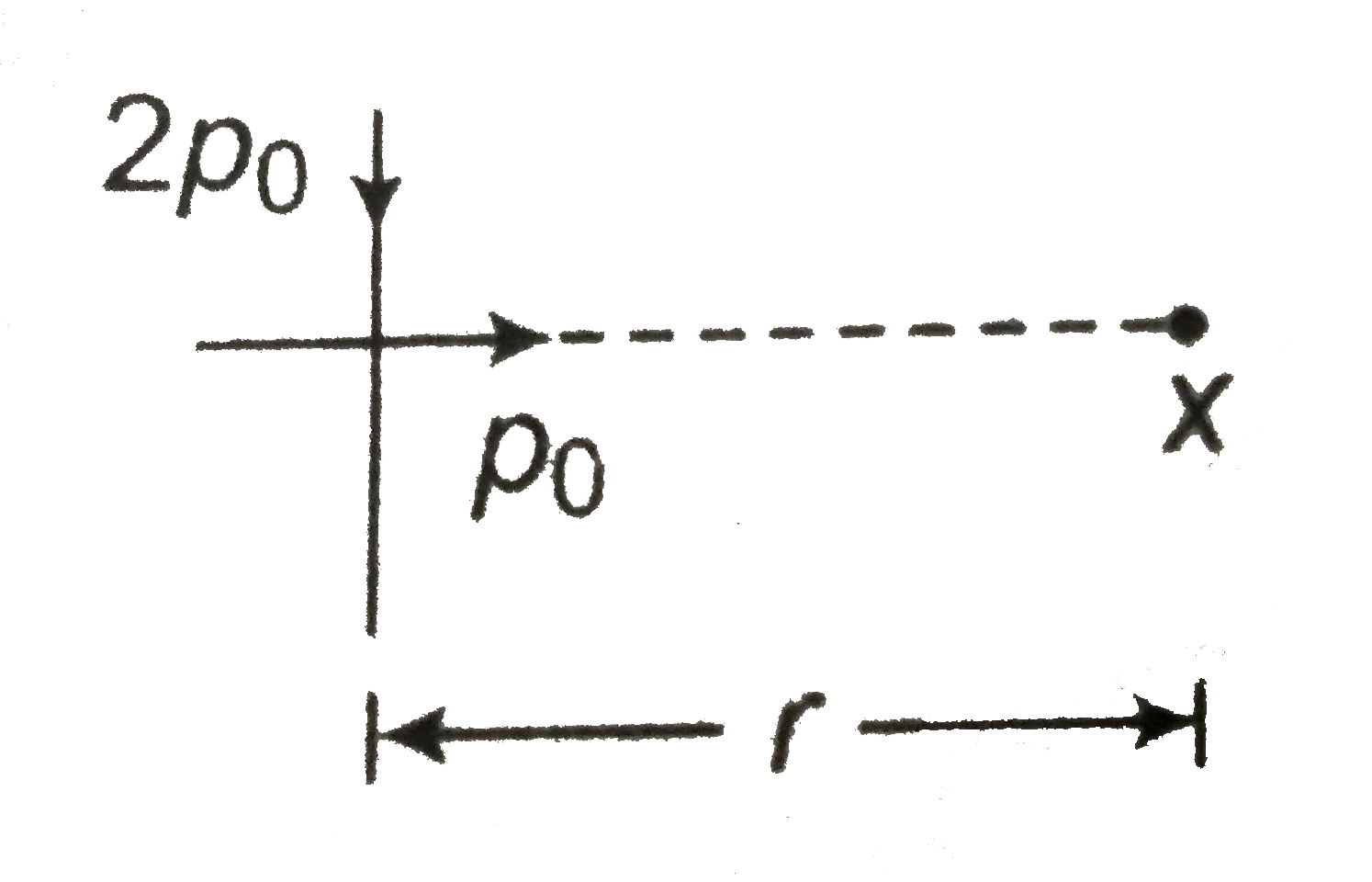
View Solution

