Nucleus A decays to B with decay constant λ1 and B decays to C with decay constant λ2. Initially at t=0 number of nuclei of A and B are 2N0 and N0 respectively. At t=to, no. of nuclei of B is 3N02 and nuclei of B stop changing. Find t0?
the value of t0is1λ1ln.43λ1λ2
the value of t0is1λ2ln.43λ1λ2
the value of NA at t0is3N02λ2λ1
the value of NA at t0is2N03λ2λ1
The correct Answer is:A, C
Step by step video, text & image solution for Nucleus A decays to B with decay constant lambda_(1) and B decays to C with decay constant lambda_(2). Initially at t=0 number of nuclei of A and B are 2N_(0) and N_(0) respectively. At t=t_(o), no. of nuclei of B is (3N_(0))/(2) and nuclei of B stop changing. Find t_(0)? by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MODERN PHYSICSBook:DC PANDEYChapter:MODERN PHYSICSExercise:for JEE Advanced (More than One Options is Correct )
Explore 1 Video
- MODERN PHYSICSBook:DC PANDEYChapter:MODERN PHYSICSExercise:Metch the column
Explore 6 Videos
- MODERN PHYSICSBook:DC PANDEYChapter:MODERN PHYSICSExercise:Integer Type Questions
Explore 17 Videos
- MAGNETISM AND MATTERBook:DC PANDEYChapter:MAGNETISM AND MATTERExercise:Medical gallery
Explore 1 Video
- MODERN PHYSICS - 1Book:DC PANDEYChapter:MODERN PHYSICS - 1Exercise:Level 2 Subjective
Explore 23 Videos
Similar Questions
A radioactive substance A having N0 active nuclei at t=0, decays to another radioactive substance B with decay constant λ1. B further decays to a stable substance C with decay constant λ2. (a) Find the number of nuclei of A,B and C time t. (b) What should be the answer of part (a) if λ1>>λ2 and λ1<<λ2
View SolutionA radioactive nucleus X decays to a nucleus Y with a decay constant λX=0.1s−1, Y further decays to a stable nucleus Z with a decay constant
λY=1/30s−1. Initially, there are only X nuclei and their number is N0=1020. Set up the rate equations for the populations of X, Y and Z. The population of Y nucleus as a function of time is given by NY(t)={N0λX/(λX−λY)}[exp(−λYt)−exp(−λXt)].
Find the time at which NY is maximum and determine the population X and Z at that instant.
View Solution
Knowledge Check
Nucleus A decays into B with a decay constant λ1 and B further decays into C with a decay constant λ2 . Initially, at t = 0, the number of nuclei of A and B were 3N0 and N0 respectively. If at t = t0 number of nuclei of B becomes constant and equal to 2N0, then
At0=1λ1ln[3λ12λ2]Bt0=1λ1lm[λ1λ2]Ct0=1λ1ln[2λ13λ2]Dt0=1λ2ln[3λ12λ2]Two radioactive materials A & B have decay constant 3λ and 2λ respectively. At t=0 the numbers of nuclei of A and B are 4N0 and 2N0 respectively then,
ATheir number of radioactive nuclei will be equal at t=ln2λBTheir decay rate will be equals at t=ln4λCTheir decay rate will be equal at t=ln3λDAt t=ln4λ the decay rate of A will be greater than that of B.At time t=0N1 nuclei of decay constant λ1&N2 nuclei of decay constant λ2 are mixed. The decay rate of the mixture at time 't' is:
AN1N2e−(λ1+λ2)tB(N1N2)e−(λ1−λ2)tC(N1λ1e−(λ1t)+N2λ2e−λ2t)DN1λ1N2λ2e−(λ1+λ2)t
Consider radioactive decay of A to B with which further decays either to X or Y, λ1,λ2 and λ3 are decay constant for A to B decay, B to X decay and Bto Y decay respectively. At t=0, the number of nuclei of A,B,X and Y are N0,N0 zero and zero respectively.
N1,N2,N3 and N4 are the number of nuclei of A,B,X and Y at any instant t.
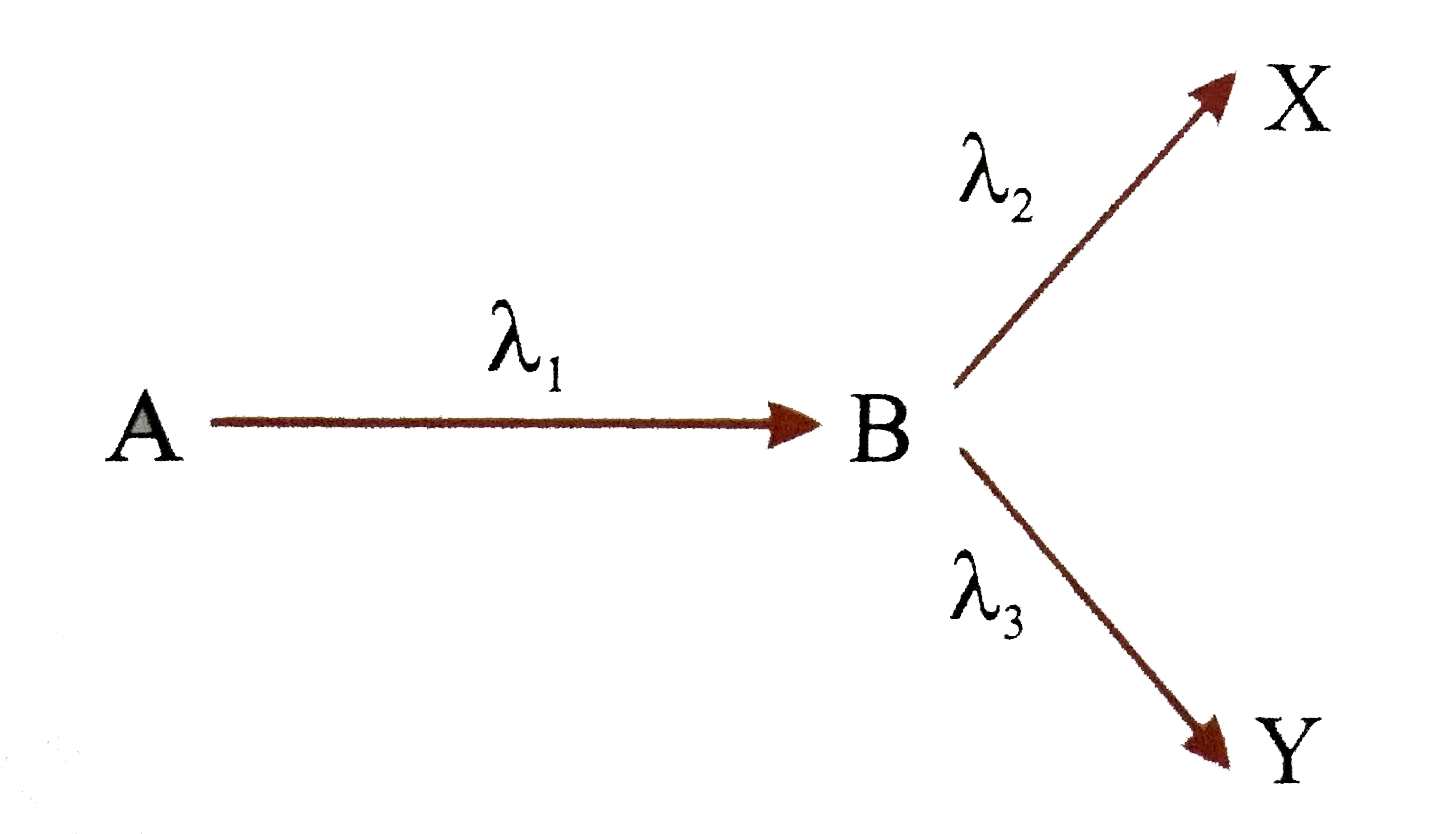
The net rate of accumulation of B at any instant is
View SolutionA radioactive element A of decay constant λA decays into another radioactive element B of decay constant λB. Initially the number of active nuclei of A was N0 and B was absent in the sample. The maximum number of active nuclei of B is found at t=2. In 2/λA. The maximum number of active nuclei of B is
View SolutionRadioactive material 'A' has decay constant '8λ' and material 'B' has decay constant 'lamda'. Initial they have same number of nuclei. After what time, the ratio of number of nuclei of material 'B' to that 'A' will be 1e ?
View SolutionRadioactive material 'A' has decay constant '8λ' and material 'B' has decay constant 'lamda'. Initial they have same number of nuclei. After what time, the ratio of number of nuclei of material 'B' to that 'A' will be 1e ?
View SolutionConsider radioactive decay of A to B with which further decays either to X or Y, λ1,λ2 and λ3 are decay constant for A to B decay, B to X decay and Bto Y decay respectively. At t=0, the number of nuclei of A,B,X and Y are N0,N0 zero and zero respectively.
N1,N2,N3 and N4 are the number of nuclei of A,B,X and Y at any instant t.
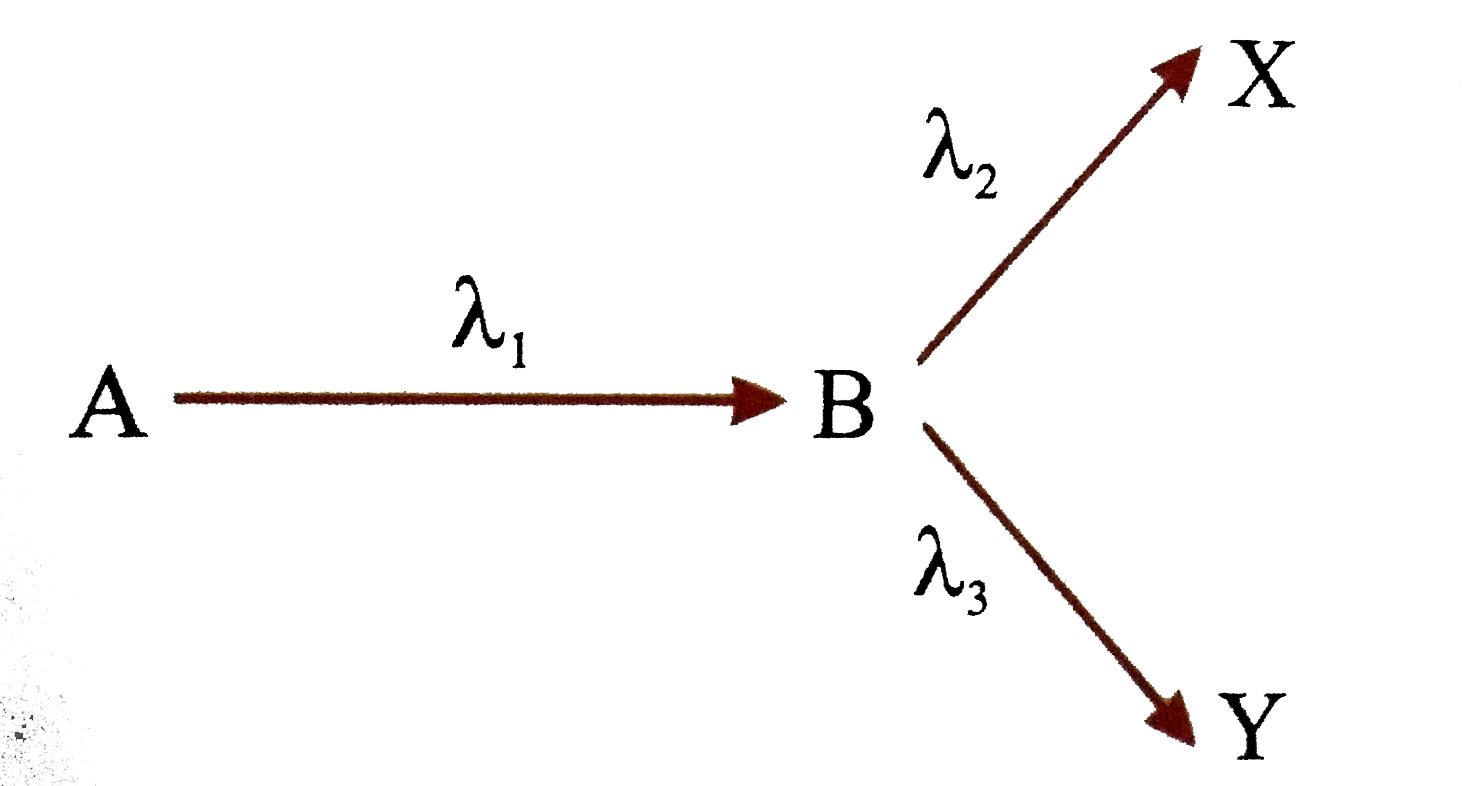
At t=∞, which of following is incorrect ?
View Solution

