Question

Tower of Hanoi, a famous Beauxbatons puzzle which consists of three towers (pegs) and more than one rings, is as depicted −

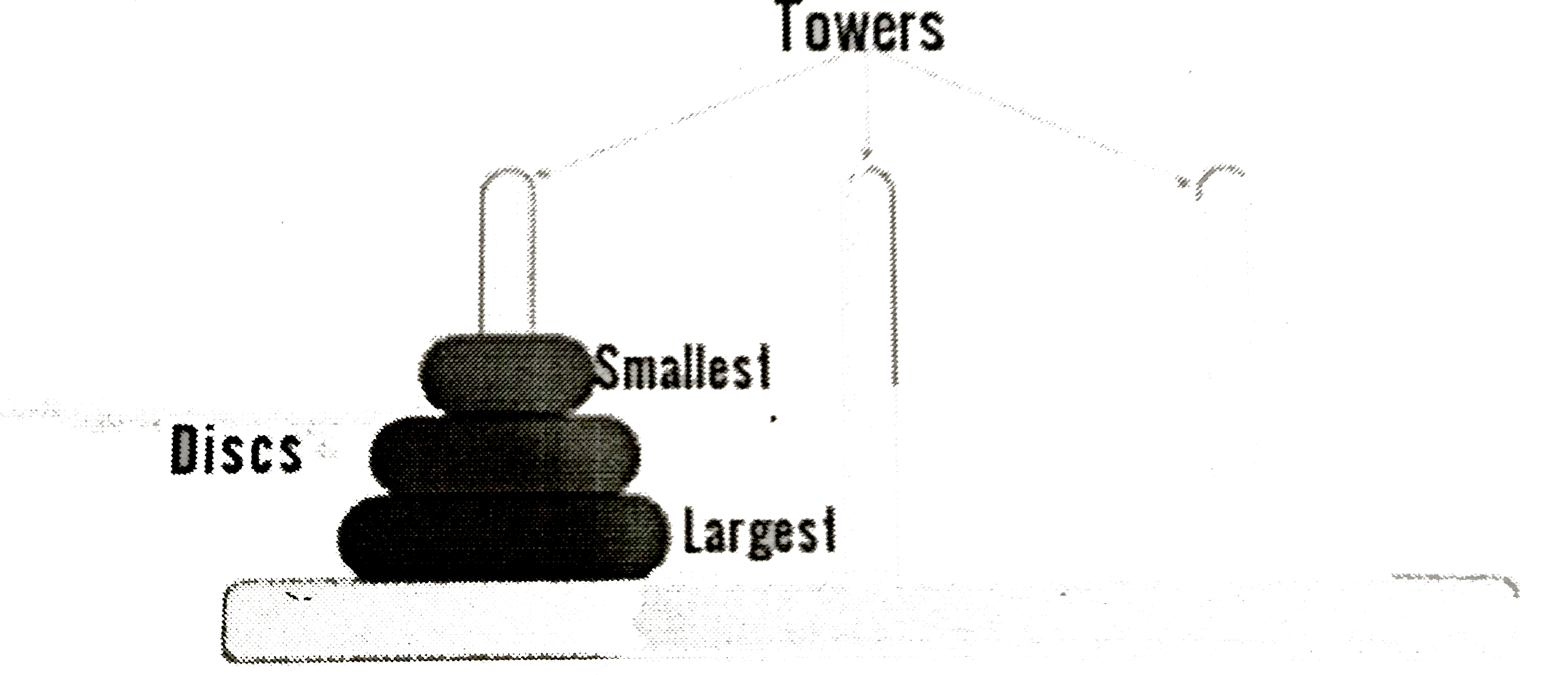
These rings are of different sizes and stacked upon in an ascending order, i.e. the smaller one sits over the larger one. There are other variations of the puzzle where the number of disks increase, but the tower count remains the same.
Rules: The mission is to move all the disks to another tower without violating the sequence of arrangement. A few rules to be followed for Tower of Hanoi are −
1. Only one disk can be moved among the towers at any given time.
2. Only the "top" disk can be removed.
3. A larger disc cannot be placed on a smaller disc. For instance if we take 3 discs in 1st peg saying it as peg A it will take 7 steps to take it to 2nd peg.
The following variation of the famous TOWER OF HANOI puzzle was offered to Fleur Delacour by Madame Maxime in order to get the location of the next puzzle by Madame Maxime which was locked inside a box.
The rules of the puzzle are essentially the same: disks are transferred between pegs one at a time. At no time may a bigger disk be placed on top of a smaller one. The difference is that now for every size there are two disks: one green and one red. Also, there are now two towers of disks of alternating colors. The goal of the puzzle is to arrange all red discs on one tower, and all green discs on another. The biggest discs at the bottom of the towers are assumed to swap positions.
For instance:

Now Fleur is given 6 discs of each colour( n = 6) arranged in the same way as the initial configuration. What are least number of moves she will need in order to get the location of the next puzzle ?

Explanation

`N =6`
No of moves is 45
Let the disks be numbered ​1,…,`N​_(1)`,…,N from smallest to largest. Without loss of generality (WLOG), suppose they are all on peg A at the start.
Disks ​N​ and ​`N_(−1)`​ are different colors, so at a minimum you must move disk `​N_(​−1)` off of disk ​N​ and onto another peg. WLOG, suppose you decide to move disk ​`N_(​−1)` to peg ​B​. In order to do that, you must first move disks ​`1,…,N_(−2​1),…,N_(−2 )` to peg ​C​.
So now you have disk ​N​ on peg ​A​, disk ​`N​_(−1)` on peg ​B​, and all the other disks on peg ​C​. You have to get disk ​`N​_(−2)` onto peg ​A​. But in order to do this you have to move all the smaller disks from peg C to peg ​B​ . Do all of this, so now you have disks ​N​ and `​N_(​−2)` on peg ​A​ and all the other disks on peg ​B​.
Fortunately, you do not have to move disk `​N_(​−3)` again, because it is already exactly where you want it (on top of disk ​`N_(​−1)`). In fact, you now have the same problem you started out with, but with ​N​−2 disks on peg ​B​ instead of ​N​ disks on peg A, and you need to move disk ​`N_(−3)`​ to peg ​A
we can make a recursive algorithm out of this, with the recursion occurring each time the number of disks to move is reduced by 2. Likewise, we can make a recursive formula to compute how many moves the algorithm will require.