Mario moves on to find a way to get through the main gates of Bowser’s chamber. He suddenly finds falling through a trapdoor and lands on something hard. The Devil Ghost Banshee , comes out and says, “This room is a standard 8×8 chessboard. Each of its 64 square is assigned a weight. These weights are assigned in such a manner that weight of a square is an average of the weight of the square that it is surrounded by.” Mario now has to determine the weights of all 64 squares and for that Banshee tells him the weights of X squares. What could be the minimum value of X with which Mario can deduce the weights of every other square?
8
32
56
None of these
To determine the minimum number of squares (X) that the Banshee must tell Mario in order to deduce the weights of all 64 squares on the chessboard, let’s analyze the situation step by step.
Step 1: Understanding the Chessboard Configuration
The chessboard is an 8×8 grid, which means it has a total of 64 squares. Each square has a weight, and the weight of a square is defined as the average of the weights of the squares that surround it.
Step 2: Analyzing the Weight Calculation
For a square located in the interior of the chessboard (not on the edge), it is surrounded by 8 other squares. The weight of that square is the average of those 8 surrounding weights. For edge squares, they are surrounded by fewer squares (5 or 6), and corner squares are surrounded by only 3 squares.
Step 3: Establishing Relationships
From the definition, we can see that if we know the weights of certain squares, we can calculate the weights of others based on the average relationship. However, if we only know the weights of a few squares, we may not be able to deduce the weights of all squares unless there is a specific configuration.
Step 4: Considering Equal Weights
If we assume that all squares have the same weight, then knowing just one square's weight would allow us to deduce the weights of all other squares. This is because if all squares are equal, the average of any surrounding squares will also equal that weight.
Step 5: Minimum Squares Required
To ensure that Mario can deduce the weights of all squares, we need to find the minimum number of squares (X) that must be known. If we can establish that all squares have the same weight, knowing just one square's weight is sufficient.
Conclusion
Thus, the minimum value of X, the number of squares that the Banshee must tell Mario, is 1. With the weight of just one square, Mario can conclude that all squares must have the same weight due to the average condition.
The chessboard is an 8×8 grid, which means it has a total of 64 squares. Each square has a weight, and the weight of a square is defined as the average of the weights of the squares that surround it.
For a square located in the interior of the chessboard (not on the edge), it is surrounded by 8 other squares. The weight of that square is the average of those 8 surrounding weights. For edge squares, they are surrounded by fewer squares (5 or 6), and corner squares are surrounded by only 3 squares.
From the definition, we can see that if we know the weights of certain squares, we can calculate the weights of others based on the average relationship. However, if we only know the weights of a few squares, we may not be able to deduce the weights of all squares unless there is a specific configuration.
If we assume that all squares have the same weight, then knowing just one square's weight would allow us to deduce the weights of all other squares. This is because if all squares are equal, the average of any surrounding squares will also equal that weight.
To ensure that Mario can deduce the weights of all squares, we need to find the minimum number of squares (X) that must be known. If we can establish that all squares have the same weight, knowing just one square's weight is sufficient.
Thus, the minimum value of X, the number of squares that the Banshee must tell Mario, is 1. With the weight of just one square, Mario can conclude that all squares must have the same weight due to the average condition.
Similar Questions
Knowledge Check
The average weight of 55 students is 55 kg , and the average weight of another 45 students is 45 kg .
Find the average weight of all the students .A48 kgB50 kgC50.5 kgD52.25 kgThe average weight of 8 men is increased by 2 kg when one of the men whose weight is 50kg is replaced by a new man the weight of the new man is
A52 kgB58kgC66 kgD68kgThe average weight of 21 boys was recorded as 64 kg. If the weight of the teacher was added, the average increased by one kg. What was the teacher's weight?
A86kgB64kgC72kgD98kg
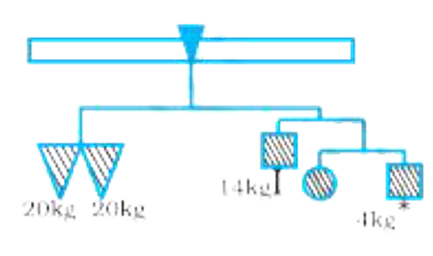
The given figure represents a weighing balance. The weights of some objects in the balance are given. Find the weight of each square and the circle .
View SolutionThe average weight of 29 students in a class is 48 kg. If the weight of the teacher is included, the average weight rises by 500 g. Find the weight of the teacher
View SolutionThe average weight of 21 boys was recorded as 64 kg. If the weight of the teacher was added, the average increased by one kg. What was the teacher's weight ?
View SolutionThe average weight of a class of 40 students is 40 kg if the weight of the teacher be included the average weight increases by 500 gms the weight of the teacher is
View SolutionThe average weight of a class of 40 boys is 55 kg. The average weight is raised to 56 kg, if the weight of teacher is added, then the weight of the teacher in kg is
View Solution
