Internal energy of an ideal diatomic gas at 300 K is 100 J. In this 100 J
potential energy = 0
rotational kinetic energy = 40 J
translational kinetic energy = 60 J
translational kinetic energy is 100 J
The correct Answer is:A, B, C
To solve the problem regarding the internal energy of an ideal diatomic gas at 300 K, we will break down the total internal energy into its components: translational kinetic energy and rotational kinetic energy.
1. Understand the Total Internal Energy:
The total internal energy U of the ideal diatomic gas is given as 100 J. For an ideal gas, the internal energy consists of kinetic energy due to translational and rotational motion.
2. Identify the Energy Distribution:
For a diatomic gas, the degrees of freedom are:
- Translational motion: 3 degrees of freedom (x, y, z directions)
- Rotational motion: 2 degrees of freedom (rotation about two axes, as rotation about the axis of the molecule does not contribute significantly)
The total degrees of freedom for a diatomic gas is 5 (3 translational + 2 rotational).
3. Calculate the Fraction of Energy:
The translational kinetic energy contributes 25 of the total internal energy, while the rotational kinetic energy contributes 35 of the total internal energy.
4. Calculate Translational Kinetic Energy:
Utranslational=25×U=25×100J=40J
5. Calculate Rotational Kinetic Energy:
Urotational=35×U=35×100J=60J
6. Summarize the Results:
- Translational kinetic energy = 40 J
- Rotational kinetic energy = 60 J
Final Answer:
- Translational Kinetic Energy: 40 J
- Rotational Kinetic Energy: 60 J
The total internal energy U of the ideal diatomic gas is given as 100 J. For an ideal gas, the internal energy consists of kinetic energy due to translational and rotational motion.
For a diatomic gas, the degrees of freedom are:
- Translational motion: 3 degrees of freedom (x, y, z directions)
- Rotational motion: 2 degrees of freedom (rotation about two axes, as rotation about the axis of the molecule does not contribute significantly)
The total degrees of freedom for a diatomic gas is 5 (3 translational + 2 rotational).
The translational kinetic energy contributes 25 of the total internal energy, while the rotational kinetic energy contributes 35 of the total internal energy.
Utranslational=25×U=25×100J=40J
Urotational=35×U=35×100J=60J
- Translational kinetic energy = 40 J
- Rotational kinetic energy = 60 J
- Translational Kinetic Energy: 40 J
- Rotational Kinetic Energy: 60 J
Topper's Solved these Questions
Similar Questions
Calculate the internal energy of one mole of a diatomic gas at 300 K. Assume the molecules to be rigid.
View SolutionAn ideal gas follows a cyclic process as shown in figure. Internal energy of gas at point A is 10 J while at B is 70 J. the heat absorbed by gas in BC is 120 J.
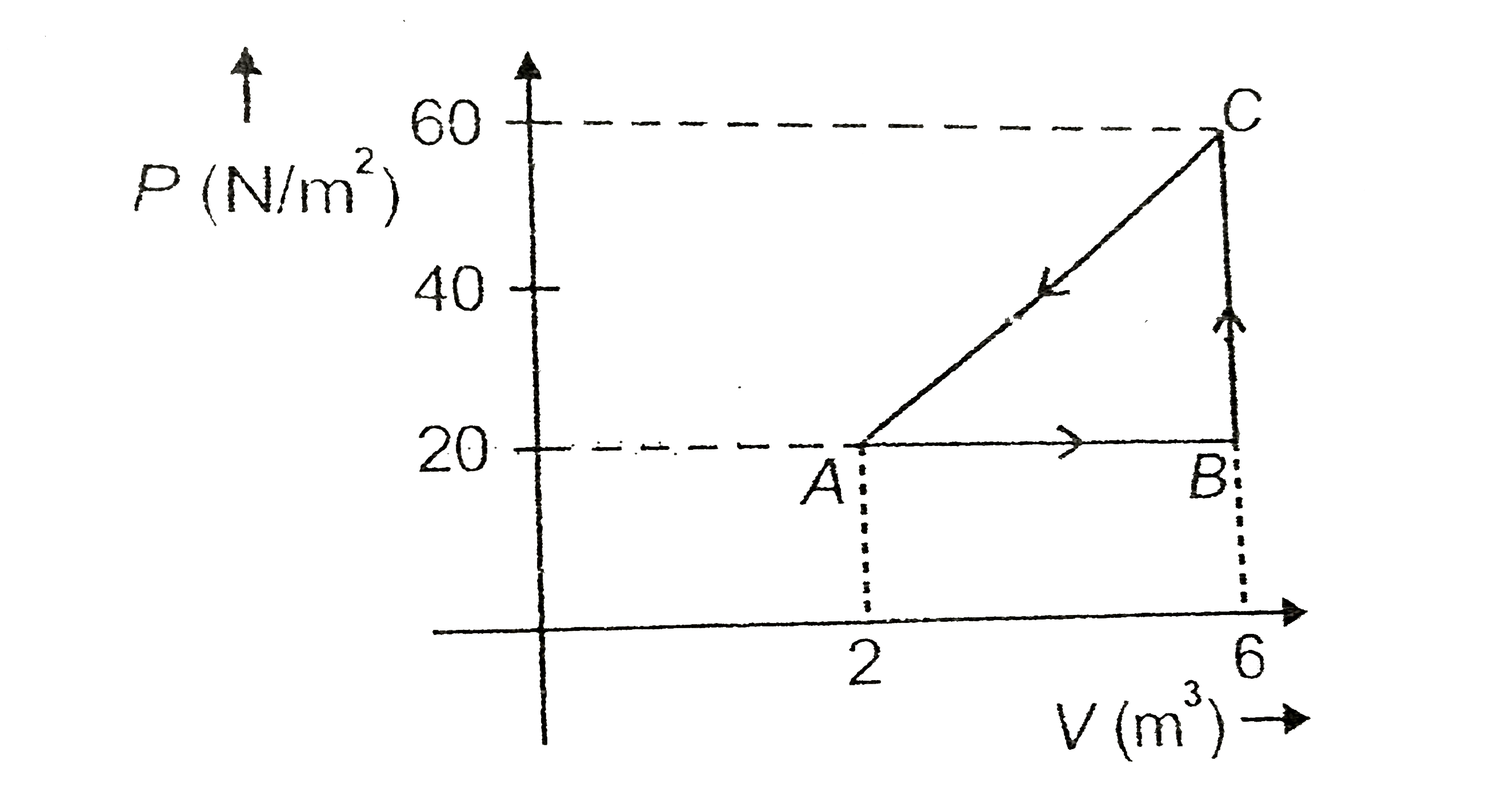
(a) How much heat is absorbed in process AB?
(b) Find heat energy rejected or absorbed by gas in process CA.
View Solution
Knowledge Check
The internal energy of one mole of the diatomic gas at 200 K is
A100 RB200 RC500 RD400 RThe internal energy of diatomic gas is due to
Arotatory motionBtranslatory motionCvibratory motionDboth 'a' and 'b'One mole of an ideal diatomic gas absorbs 1831.4 J of heat and does 1000 J of work at 27∘C. What is the change in temperature observed ?
A25∘CB40∘CC37∘CD67∘C
The mean kinetic energy of a gas at 300K is 100J .The mean energy of the gas at 450K" is equal to (A) 100J (B) 3000J (C) 450J (D) 150J
View SolutionIf 21 J of heat energy is supplied to an ideal diatomic gas at constant pressure, then the change in its energy is
View SolutionFind the change in internal energy if heat supplied to the gaseous system is 100 J and work done by the system is 80 J.
View SolutionThe temperature of an ideal gas is increased for 100 k to 400k. If at 100 K the root mean square velocity of the gas molecules is v, at 400K it becomes
View SolutionIf 21 J of heat energy is supplied to an ideal diatomic gas at constant pressure, then the change in its energy is
View Solution

