Five identical cells are connected in parallel. Now, polarity of one of the cells is reversed. Percentage change in equivalent emf will be
-0.1
-0.2
-0.4
-0.6
The correct Answer is:C
To solve the problem of finding the percentage change in equivalent EMF when one of the five identical cells connected in parallel has its polarity reversed, we can follow these steps:
1. Understand the Configuration:
- We have 5 identical cells connected in parallel. Let the EMF of each cell be E and the internal resistance of each cell be R.
2. Calculate Initial Equivalent EMF:
- When all cells are connected in parallel, the equivalent EMF (Eeq) is simply the EMF of one cell, since they are identical and in parallel:
Eeq_initial=E
3. Effect of Reversing One Cell:
- When the polarity of one cell is reversed, its EMF becomes −E. Thus, we now have:
- Four cells with EMF E
- One cell with EMF −E
4. Calculate New Equivalent EMF:
- The equivalent EMF can be calculated using the formula:
Eeq_new=ER+ER+ER+ER−ER
- This simplifies to:
Eeq_new=4E−ER=3ER
- The total resistance in the parallel circuit remains:
Req=R5(since there are 5 identical resistances in parallel)
5. Final Equivalent EMF:
- Therefore, the new equivalent EMF is:
Eeq_new=3E5
6. Calculate Percentage Change in EMF:
- The change in EMF (ΔE) is given by:
ΔE=Eeq_new−Eeq_initial=3E5−E=3E−5E5=−2E5
- To find the percentage change:
Percentage Change=(ΔEEeq_initial)×100=⎛⎝−2E5E⎞⎠×100=−40%
Conclusion:
The percentage change in equivalent EMF when one cell's polarity is reversed is −40%, indicating a decrease in EMF.
- We have 5 identical cells connected in parallel. Let the EMF of each cell be E and the internal resistance of each cell be R.
- When all cells are connected in parallel, the equivalent EMF (Eeq) is simply the EMF of one cell, since they are identical and in parallel:
Eeq_initial=E
- When the polarity of one cell is reversed, its EMF becomes −E. Thus, we now have:
- Four cells with EMF E
- One cell with EMF −E
- The equivalent EMF can be calculated using the formula:
Eeq_new=ER+ER+ER+ER−ER
- This simplifies to:
Eeq_new=4E−ER=3ER
- The total resistance in the parallel circuit remains:
Req=R5(since there are 5 identical resistances in parallel)
- Therefore, the new equivalent EMF is:
Eeq_new=3E5
- The change in EMF (ΔE) is given by:
ΔE=Eeq_new−Eeq_initial=3E5−E=3E−5E5=−2E5
- To find the percentage change:
Percentage Change=(ΔEEeq_initial)×100=⎛⎝−2E5E⎞⎠×100=−40%
The percentage change in equivalent EMF when one cell's polarity is reversed is −40%, indicating a decrease in EMF.
Topper's Solved these Questions
Similar Questions
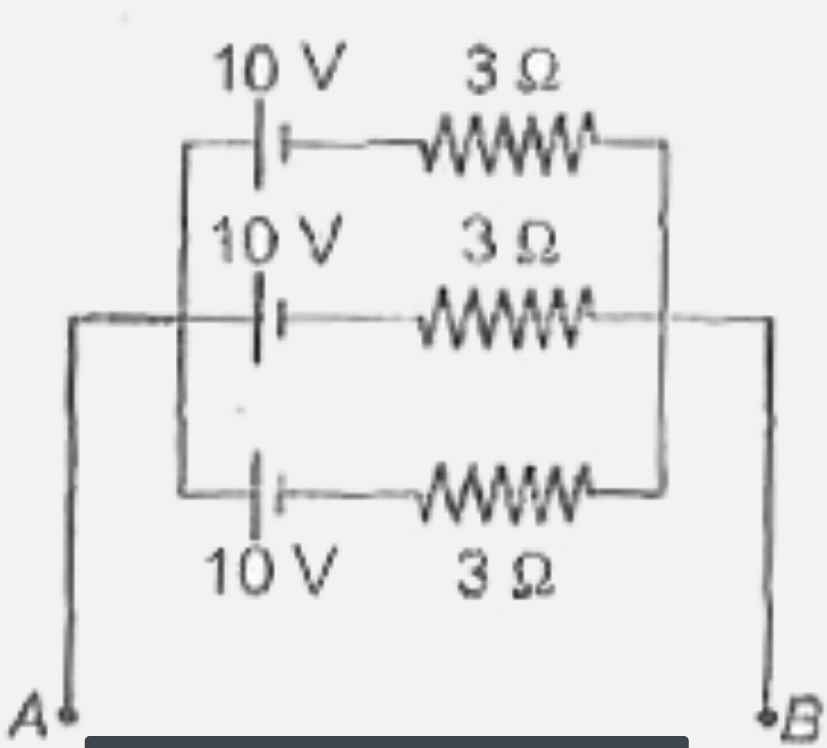
Three identical cells are connected in parallel across AB. Net potential across AB is
View SolutionFour identical cells of emf ε and internal resistance r are to be connected in series. Suppose, if one of the cell is connected wrongly, then the equivalent emf and effective internal resistance of the combination is
View Solution
Knowledge Check
When cells are connected in parallel then
AThe current decreasesBThe curretn increasesCThe e.m.f. increasesDThe e.m.f decreasesTwenty cells each of emf E and internal resistance r are connected in series to form a loop . If polarity of one of the cell is reserved, then terminal potential across this cell is
A19E10B11E10C9E10DZeroIn a arrangement, 3n cells of emf ε and internal resistance r are connected in series. Out of 3n cells polarity of n cells is reversed. Current in the circuit is
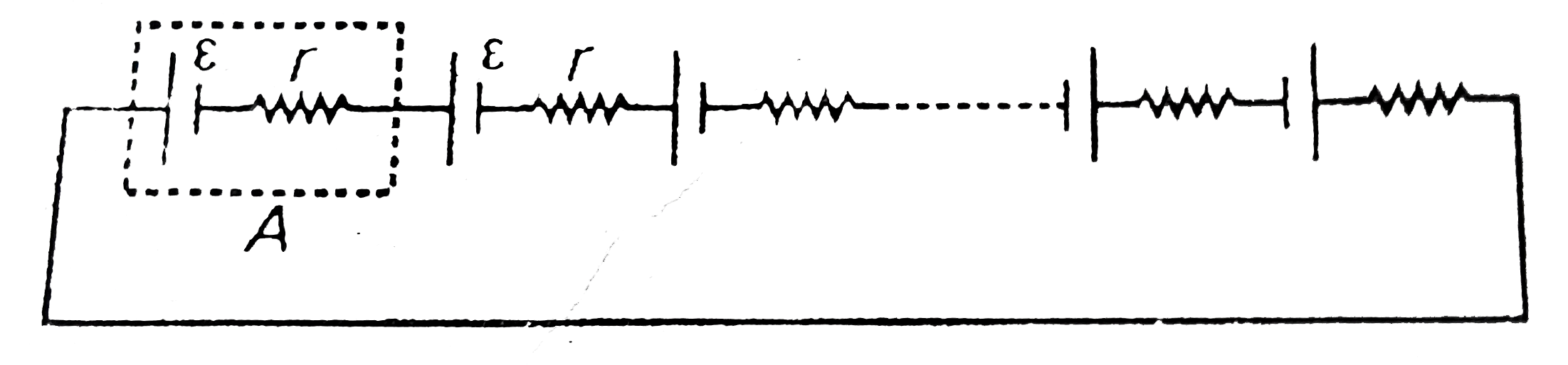 A2εlorB2ε3rCε3rDεr
A2εlorB2ε3rCε3rDεr
The equivalent resistance of n identical resistors connected in parallel is x. If the resistors are connected in series, the equivalent resistance would be
View SolutionThe equivalent resistance of n identical resistors connected in parallel si x. If the resistors are connected in series, the equivalent resistance would be.
View SolutionTwo cells when connected in series are balanced on 8m on a potentiometer. If cells are connected with polarities of one the cell reversed, they balance on 2m. The ratio of e.m.f.'s of the two cells
View SolutionThree identical cells of e.m.f. 1.5V are connected in parallel. The total e.m.f. of the combination is _____.
View SolutionSix identical cells are connected as shown in the cir-cuit. The total e.m.f is ______
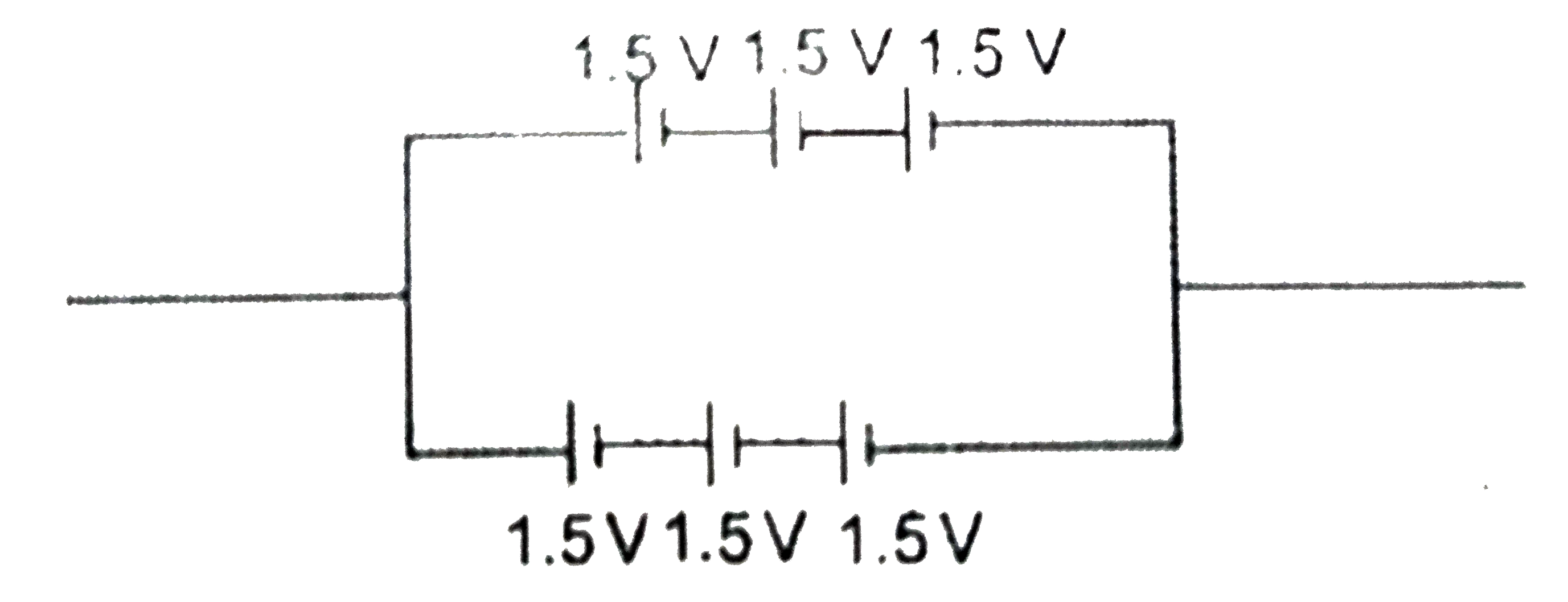
View Solution

