A point charge q is placed at a distance of r from cebtre of an uncharged conducting sphere of rad R(<r). The potential at any point on the sphere is
zero
14πε0qr
14πε0qRr2
14πε0qr2R
The correct Answer is:B
To solve the problem of finding the potential at any point on the surface of an uncharged conducting sphere with a point charge q placed at a distance r from its center (where R<r), we can follow these steps:
Step 1: Understand the Configuration
We have a point charge q located outside an uncharged conducting sphere of radius R. The distance from the center of the sphere to the point charge is r, and it is given that r>R.
Step 2: Identify the Induced Charges
When the point charge q is placed near the conducting sphere, it induces charges on the surface of the sphere. Specifically, a negative charge will be induced on the side of the sphere closest to the point charge, and a positive charge will be induced on the opposite side. The total charge on the sphere remains zero since it was initially uncharged.
Step 3: Electric Field Inside the Conductor
Inside a conductor in electrostatic equilibrium, the electric field is zero. This means that the induced charges rearrange themselves in such a way that they cancel out any electric field within the conducting material.
Step 4: Potential Inside the Conductor
Since the electric field inside the conductor is zero, the potential throughout the conductor (including at any point on the surface) is constant. This constant potential is equal to the potential at the surface of the sphere.
Step 5: Calculate the Potential at the Surface
To find the potential at the surface of the sphere, we can calculate the potential due to the point charge q at a distance r (the distance from the point charge to the center of the sphere). The formula for the electric potential V due to a point charge is given by:
V=kqr
where k is the Coulomb's constant.
Step 6: Conclusion
The potential at any point on the surface of the conducting sphere is equal to the potential due to the point charge q at the distance r:
Vsphere=kqr
Summary
Thus, the potential at any point on the surface of the sphere is given by:
V=kqr
We have a point charge q located outside an uncharged conducting sphere of radius R. The distance from the center of the sphere to the point charge is r, and it is given that r>R.
When the point charge q is placed near the conducting sphere, it induces charges on the surface of the sphere. Specifically, a negative charge will be induced on the side of the sphere closest to the point charge, and a positive charge will be induced on the opposite side. The total charge on the sphere remains zero since it was initially uncharged.
Inside a conductor in electrostatic equilibrium, the electric field is zero. This means that the induced charges rearrange themselves in such a way that they cancel out any electric field within the conducting material.
Since the electric field inside the conductor is zero, the potential throughout the conductor (including at any point on the surface) is constant. This constant potential is equal to the potential at the surface of the sphere.
To find the potential at the surface of the sphere, we can calculate the potential due to the point charge q at a distance r (the distance from the point charge to the center of the sphere). The formula for the electric potential V due to a point charge is given by:
The potential at any point on the surface of the conducting sphere is equal to the potential due to the point charge q at the distance r:
Thus, the potential at any point on the surface of the sphere is given by:
Topper's Solved these Questions
- ELECTROSTATICSBOOK - DC PANDEYCHAPTER - ELECTROSTATICSEXERCISE - JEE Advanced
44 Videos
- ELECTROSTATICSBOOK - DC PANDEYCHAPTER - ELECTROSTATICSEXERCISE - Comprehension
36 Videos
- ELASTICITYBOOK - DC PANDEYCHAPTER - ELASTICITYEXERCISE - Medical entrances s gallery
21 Videos
- EXPERIMENTSBOOK - DC PANDEYCHAPTER - EXPERIMENTSEXERCISE - Subjective
15 Videos
Similar Questions
A point charge q has been placed at a distance x from the centre of a neutral solid conducting sphere of radius R(x gt R). Find the potential of the sphere. How will your answer change if the sphere is not solid, rather it is a thin shell of conductor.
View SolutionA point charge Q is situated (outside) at a distance r from the centre of an uncharged conducting solid sphere of radius R. The potential due to induced charges (on the conductor) at a point B inside the conductor whose distance form the point charge is d is ______
View Solution
Knowledge Check
The potential at a distance R/2 from the centre of a conducting sphere of radius R will be
A0BQ8πε0RCQ4πε0RDQ2πε0R
A point charge q'q is placed at distance 'a' from the centre of an uncharged thin spherical conducting shell of radius R=2a. A point 'P' is located at a distance 4a from the centre of the conducting shell as shown. The electric potential due to induced charge on the inner surface of the conducting shell at point 'P' isAkq5aB−kq5aCkq4aD−kq4aA point charge q is placed at a distance of r from the centre O of an uncharged spherical shell of inner radius R and outer radius 2R. The electric potential at the centre of the shell will be
 Aq4πε0(1r−12R)Bq4πε0rCq4πε0(1r+12R)DNone of these
Aq4πε0(1r−12R)Bq4πε0rCq4πε0(1r+12R)DNone of these
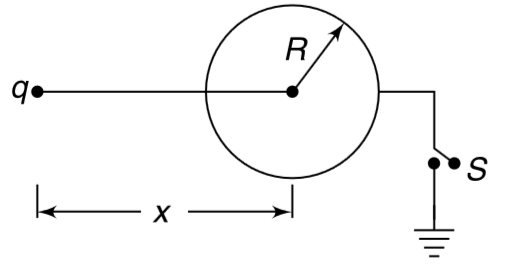
A point charge q is placed at a distance x from the centre of a conducting sphere of radius R(lt x). (a) How much charge will flow through the switch S when it is closed to ground the sphere? (b) Find the current through the switch S when charge ‘q’ is moved towards the sphere with velocity V.
View SolutionA point charge +q is held at a distance R from the centre of an uncharged spherical conductor of radius a(a<R). Calculate the potential of the conductor in the presence of q.
View SolutionA point charge +q is held at a distance R from the centre of an uncharged spherical conductor of radius a(a<R). Calculate the potential of the conductor in the presence of q.
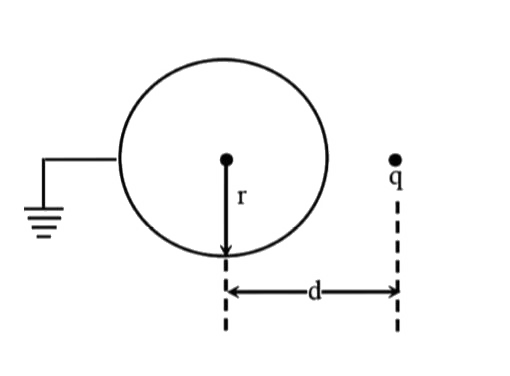
View SolutionA point charge q is placed at some distance d away from the centre of a grounded conducting sphere of radius r, as shown in the figure. The charge that flows the earth to the sphere is
View SolutionA charge q is placed at a distance of 2R from the centre of a spherical conducting shell of radius R. What is electrical potential, due to charges induced on the shell, at a point which is farthest from the point charge ?
View Solution
