दो आवेशित चालकों की धारिताएँ क्रमशः C1 और C2 हैं। उन्हें Q1 और Q2 आवेश देने पर उनके विभव क्रमशः V1 और V2 हो जाते हैं। यदि उन्हें तार से जोड़ दिया जाये, तो निम्नलिखित की गणना कीजिए-(i) उभयनिष्ठ विभव, (ii) संयोजन में ऊर्जा ह्रास।

(i) उभयनिष्ठ विभव-मानलो A और B दो विलगित चालक हैं, जिनकी धारिताएँ क्रमशः C1 और C2 हैं। इन चालकों को क्रमशः Q1 और Q2 आवेश देने पर उनके विभव क्रमशः V1औरV2 हो जाते हैं।
अतः कुल आवेश
Q=Q1+Q2 ....(1)
परन्तु Q1=C1V1
Q2=C2V2
समी. (1) में मान रखने पर,
Q=C1V1+C1V2
दोनों चालकों की कुल धारिता
C=C1+C2
मानलो दोनों चालकों को तार द्वारा जोड़ने पर उनका उभयनिष्ठ विभव V हो जाता है।
अतः सूत्र Q = CV से,
Q1+Q2=(C1+C2)V
V=Q1+Q2C1+C2
V=C1V1+C2V2C1+C2
यही उभयनिष्ठ विभव के लिए व्यंजक है।
(ii) संयोजन में ऊर्जा ह्रास-दोनो लकों को जोड़ने से पहले A और B की कुल ऊर्जा,
U1=12C1V21+12C2V22
दोनों चालकों को जोड़ने के बाद A और B की कुल ऊर्जा
U2=12C1V2+12C2V2
=12(C1+C2)V2
=12(C1+C2)(C1V1+C2V2C1+C2)2
=12(C1V1+C2V2)2C1+C2
∴U1+C2=(12C1V21+12C2V22)−12(C1V1+C2V2)2C1+C2
=12[(C1V21+C2V22)(C1+C2)−(C1V1+C2V2)2C1+C2]
=12[C1C2V21+C1C2V22−2C1C2V1V2C1+C2]
=12.C1C2C1+C2[V21+V22−2V1V2]=C1C22(C1+C2)(V1+V2)2
चूँकि (V1−V2)2 धनात्मक है, अत: U1−U2 भी धनात्मक होगा। अतः आवेश के पुनर्वितरण में सदैव ऊर्जा का ह्रास होता है।
इस प्रकार, ऊर्जा ह्रास =C1C22(C1+C2)(V1−V2)2
Topper's Solved these Questions
- स्थिर विधुत विभव एवं धारिताBook:YUGBODHChapter:स्थिर विधुत विभव एवं धारिताExercise:आंकिक प्रश्न
Explore 14 Videos
- स्थिर विधुत विभव एवं धारिताBook:YUGBODHChapter:स्थिर विधुत विभव एवं धारिताExercise:लघु उत्तरीय प्रश्न
Explore 31 Videos
- विविकरण तथा द्रव्य की द्वैत प्रकृतिBook:YUGBODHChapter:विविकरण तथा द्रव्य की द्वैत प्रकृतिExercise:आंकिक प्रश्न
Explore 5 Videos
Similar Questions
क्या 1 सेमी त्रिज्या का धातु का.गोला एक कूलॉम आवेश धारण कर सकता है ?
View Solutionविद्युत् विभव किसे कहते हैं? यह अदिश राशि है या सदिश राशि?
View Solutionएक इलेक्ट्रान 100 वाल्ट तक त्वरित किया जाता है। इसकी गतिज ऊर्जा ज्ञात कीजिये।
View Solutionआकृति में PQ तथा RS एक वृत्त पर क्रमशः बिन्दु A और C पर स्पर्श रेखाएं है। यदि ∠ABC=60∘ और ∠BAP=40∘ हो तो ∠BCR ज्ञात कीजिए।

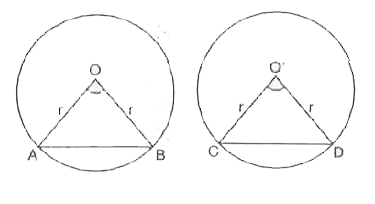
View Solutionआकृति में आपको दो वृत्त क्रमशः C(O, r) और C(O' r) दिए गए हैं| यदि उनकी संगत जीवाओं की लम्बाइयों में 1:1 का अनुपात हो तो उनके संगत केंद्रों में अंतरिक कोणों का अनुपात ज्ञात कीजिए |
View SolutionPre board special|विभव प्रवणता और आवेशित कण की ऊर्जा पर आधारित प्रश्न
View Solutionसंकेंद्रित कोशों के कारण विभव | चालकों में आवेश स्थानांतरण चालकों की अर्थिंग
View Solutionउत्पत्ति की दृष्टि से 'ऑनलाइन' और 'शिक्षा' शब्द है, क्रमशः
View Solutionदो अनन्त लम्बाई के समान्तर तार जिन पर रेखीय आवेश घनत्व क्रमश: λ1, औरλ2 , हैं R मीटर की दूरी पर रखे हैं, उनमें से किसी एक की एकांक लम्बाई पर बल होगा
View Solutionअभिक्रियाओं के निम्नलिखित अनुक्रम पर विचार कीजिए: मध्यवर्ती उत्पाद (X) और (Y) क्रमशः हैं:
View Solutionयदि 4f में त्रिज्य नोडों और कोणीय नोडों की संख्या क्रमशः X और Y हैं। X + Y का योग ज्ञात कीजिए?
View Solutionयदि A और B, क्रमशः 10 और 20 BOD के साथ जल के दो नमूने हैं, तब सही विकल्प चिह्नित कीजिए।
View Solutionफ्लोरीन, क्लोरीन, ब्रोमीन और आयोडीन की इलेक्ट्रॉन लब्धि एन्थैल्पी (kJ/mol में) क्रमशः हैं:
View Solutionबोरिक अम्ल में बोरॉन और ऑक्सीजन परमाणुओं के संकरण की अवस्था क्रमशः हैं:
View Solutionअम्लीय, क्षारीय और उभयधर्मी ऑक्साइड, क्रमशः हैं:
View Solutionसेल के मानक विभव की गणना कीजिए, यदि Zn2+/Zn और Ag+/Ag के मानक इलेक्ट्रॉड विभव क्रमश: - 0.763 V और + 0.799 V हैं।
View Solution

