भिन्न - भिन्न तापों T1 एवं T2 के दो पिंडों को यदि ऊष्मीय सम्पर्क में लाया जाए तो आवश्यक नहीं कि उनका अंतिम ताप (T1+T22) ही हो । क्यों ?
क्योंकि दोनों पिंडों के द्रव्यमान एवं विशिष्ट उष्माएँ भिन्न - भिन्न हो सकते है । औसत ताप T1+T22तभी सम्भव है जब दोनों की द्रव्यमान धारिताएँ समान हो ।
Topper's Solved these Questions
- ऊष्मागतिकीBook:YUGBODHChapter:ऊष्मागतिकीExercise:लघु उत्तरीय प्रश्न
Explore 16 Videos
- ऊष्मागतिकीBook:YUGBODHChapter:ऊष्मागतिकीExercise:दीर्घ उत्तरीय प्रश्न
Explore 1 Video
- ऊष्मागतिकीBook:YUGBODHChapter:ऊष्मागतिकीExercise:वस्तुनिष्ठ प्रश्न ( (IV) रिक्त स्थान )
Explore 7 Videos
- अणुगति सिद्धांत Book:YUGBODHChapter:अणुगति सिद्धांत Exercise:आंकिक प्रश्न
Explore 7 Videos
- कणों के नियम तथा घूर्णी गति Book:YUGBODHChapter:कणों के नियम तथा घूर्णी गति Exercise:आंकिक प्रश्न
Explore 7 Videos
Similar Questions
समतापी तथा रुद्धोष्म प्रक्रम में भिन्नताएं लिखिए ।
View Solutionआदर्श गैस के कार्नो इंजन का सूचक आरेख खींचकर प्रत्येक परिवर्तन को समझाइये ।
View Solution…………… कार्य के उस परिमाण के बराबर होता है जो एकांक ऊष्मा उत्पन्न करने के लिए आवश्यक है ।
View Solutionस्थिर दाब पर 27∘C ताप पर किसी आदर्श गैस का आयतन दुगुना करने के लिए उसे किस ताप तक गर्म करना पड़ेगा ?
View Solution2m त्रिज्या के एक वलय (छल्ले ) का भार 100 kg है। यह एक क्षैतिज फर्श पर इस प्रकार लोटनिक गति करता है कि इसके द्रव्यमान केन्द्र की चाल 20 cm/s हो। इसको रोकने के लिये कितना कार्य करना होगा ?
View SolutionIf the normals at points t1andt2 meet on the parabola, then t1t2=1 (b) t2=−t1−2t1 t1t2=2 (d) none of these
View Solution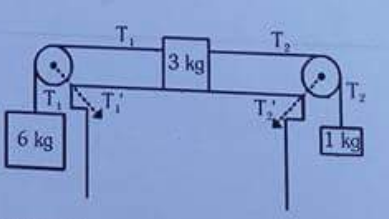
Calculate a, T1,T2,T1'&T2'.
View Solutionदर्शाइए कि परवलय y2=4ax पर बिंदुओं t1,t2 और t3 से बने त्रिभुज के क्षेत्रफल का परिमाण a2(t1−t2)(t2−t3)(t3−t1) है।
View SolutionIf the tangents at t1andt2 to a parabola y2=4ax are perpendicular then (t1+t2)2−(t1−t2)2=
View Solutionआइये हम त्रिभुजीय संख्याओं को पुनः देखे ( आकृति A 1.2 ) दो क्रमागत संख्याओं को जोड़िये। उदाहरण के लिए , T1+T2=4,T2+T3=9,T3+T4=16
T4+T5 के बारे में आपका क्या कहना है ?
Tn−1+Tn का एक कंजेक्चर बनाइये।
View SolutionThe area of triangle formed by the points points and t1,t2 and t3 on y3 =4ax is k|(t1−t2)(t2−t3)(t3−t1)| then K =
View SolutionSuppose
(x+a)n=T0+T1+T2+…+Tn
Then (T0−T2+T4−…)2+(T1−T3+T5−….)2 is equal to
View Solutionयदि (x+a)n के विस्तार में, T0,T1,T2,…. पद प्राप्त होते है, तो (T0−T2+T4−…)2+(T1−T3+T5−….)2 बराबर होगा
View SolutionIf t_(1)+t_(2)+t_(3)=-t_(1)t_(2)t_(3) , Then points [at_(1)t_(2),a(t_(1)+t_(2))] , [at_(2)t_(3),a(t_(2)+t_(3))] And [at_(3)t_(1),a(t_(3)+t_(1))] The perpendicular of the triangle with vertices will be
View SolutionThe tangents at the points (at21,2at1),(at22,2at2) are right angles if
View Solutionयदि किसी भिन्न का अंश, हर से 2 कम है और यदि हर में 1 जोडा जाए तो यह 12 हो जाता है तब वह भिन्न होगी ?
View Solution

