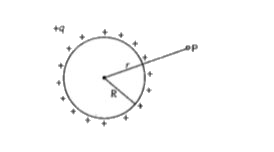
Electric intensity at a point outside a charged spherical conductor surrounded by air is 6 N/C. If the space around the conductor is filled with a medium of dielelctric constant 3, then the electric intensity at the same point will be

20 N/C

2 N/C

2.5 N/C

6.25 N/C

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Updated on:21/07/2023

Answer

Step by step video, text & image solution for Electric intensity at a point outside a charged spherical conductor surrounded by air is 6 N/C. If the space around the conductor is filled with a medium of dielelctric constant 3, then the electric intensity at the same point will be by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 PHYSICS ELECTRIC CHARGES AND FIELDS

Topper's Solved these Questions

Knowledge Check

Electric field intensity at a point a hollow charged spherical conductor
Ais zero
Bis constant
Cincrease with the distance from the centre of the sphere
Dnone of these
Electric intensity at a point just outside a charged conductor of any shape is
A $\frac{σ}{\in_{0} K}$
B $\frac{σ}{2 \in_{0} K}$
C $\frac{2 σ}{\in K}$
D $\frac{σ^{2}}{2 \in K}$
Electric intensity at a point near a charged sphere of charge q is given by
A $E = \frac{1}{4 π \in_{0} K} \cdot \frac{q}{r^{2}}$
B $E = \frac{1}{2 π \in_{0} K} \cdot \frac{q}{r}$
C $E = \frac{σ}{\in_{0} k}$
Dnone of these