A connector can slide without frictiion along a -shaped conductor located in a horizontal plane (Fig). The connector has a length , mass and resistance . The whole system is located in a unifrom magnetic field of induction directed vertically. At the moment a constant horizontal force starts acting on the connector shifting it translationwise to the right. Find how th e velocity o fhte connector varies with time . The inductance of the loop and the resistance of the II-shaped conductor conductor are assumed to be negligible
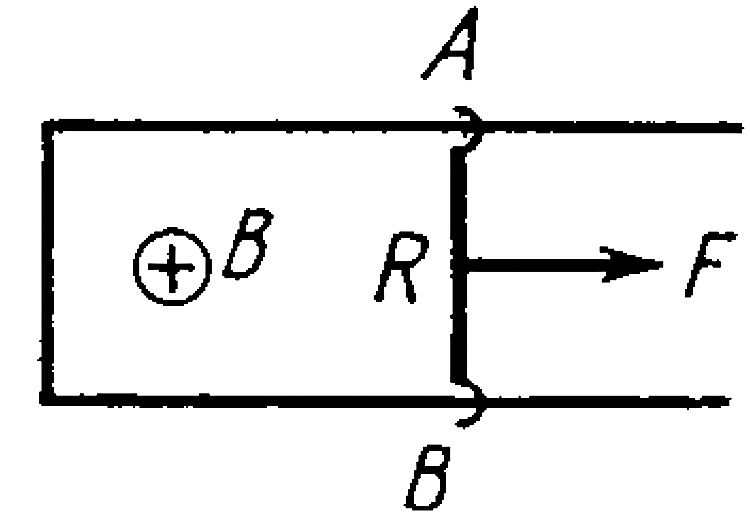
Step by step video & image solution for A connector AB can slide without frictiion along a II-shaped conductor located in a horizontal plane (Fig). The connector has a length l, mass m and resistance R. The whole system is located in a unifrom magnetic field of induction B directed vertically. At the moment t = 0 a constant horizontal force F starts acting on the connector shifting it translationwise to the right. Find how th e velocity o fhte connector varies with time t. The inductance of the loop and the resistance of the II-shaped conductor conductor are assumed to be negligible by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
A copper connector of mass m slides down two smooth cooper bars, set at an angle α to the horizontal due to gravity (Fig). At the top the bars is equal to l. The system is located in a unifrom magnetic field of induction B, perpendicular to the plane in which the connector slides. The resistances of the bars, the connector and the sliding contacts, as well as the self-inductance of the loop, are assumed to be negligible. Find the steady-state velocity of the connector.

View SolutionA wire bent as a parabola y=ax2 is located in a uniformed magnetic field of induaction B , the vector B being perpendicular to the plane x−y . At moment t=0 a connector starts sliding translationwise from the parabola apex with a constant acceleration ω . Find the emf of electromagnetic induction in the loop thus formed as a function of y

View Solution
Knowledge Check
A straight conductor carrying current I and a loop closed by a sliding connector of resistance R lie in the same plane . The connector slides towards right with a uniform velocity v . The induced current generated in the loop in terms of distance r of the connector from the straight conductor will be __
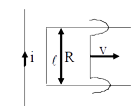 Aμ0ilv2πrBμ0il2πrCμ0ilv2πrRDNone of these
Aμ0ilv2πrBμ0il2πrCμ0ilv2πrRDNone of theseA conducting wire of length l and mass m can slide without friction on two parallel rails and is connected to capacitance C. The whole system lies in a magnetic field B and a constant force F is applied to the rod. Then
Athe rod moves with constant velocityBthe rod moves with an acceleration of Fm+B2l2CCthere is constant charge on the capacitor.Dcharge on the capacitor increases with time
A conductor rod AB of mass m slides without friction over two long conducting rails separated by a distance (Fig) At the left end the raidls are interconnected by a resistance R. The system is located in a unifrom magnetic fileld perpendicular to the plane of the loop. At the moment t=0 the rod AB starts moving to the right with an initial velocity v0. Neglecting the resistances of the rails and the rod AB, as wellas the self -indcuctance, find:
(a) the distance covered by the rod until it comes to a standsill,
(b) the amount of heat generated in the resitance R during this process.
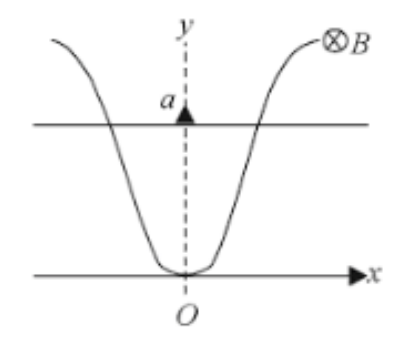
View SolutionA wire bent as a parabola y=kx2 is located in a uniform magnetic field of induction B, the vector B being perpendicular to the plane xy. At t=0, the sliding wire starts sliding from the vertex O with a constant acceleration a linearly as shown in Fig. Find the emf induced in the loop -
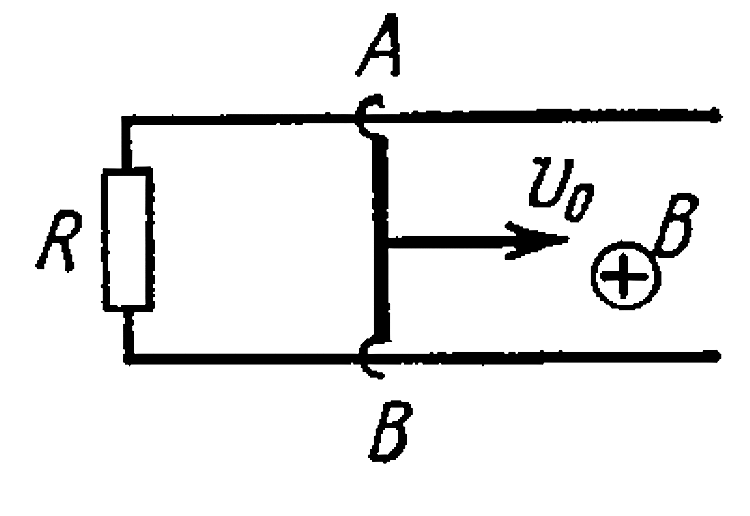
View SolutionA long straight wire carrying a current I and a II- shaped conductor with siding connector are located in the same plane as shown in Fig. The connector of length l and resistance R sides to the right with a current induced in the loop as a function of separation r between the connector and the stragiht wire. The resistance of the II-shaped conductor and the self-induced of the loop are assumed to be negligible.

View SolutionA coil of inductance L connects the upper ends of two vertical copper bars separated by a distance l . A horizontal conducting connnector of mass m starts falling with zero initial velocit along the bars without losing contact with them. The whole system is located in a uniform magnetic field with induction B perpendicular to the plane of the bars. Find the law of motion x(t) of the connector.
View SolutionA copper connector of massm, starting from rest, slides down two conducting bars set at angle α to the horizontal, due to gravity (see figure). At the top the bars are interconnected trhough a resistance R. The separation between the bars is equal to l. The system is located in uniform magnetic field of induction B, perpendicular to the plane in which the connectr slides. The resistance of the bars the connector and the sliding contacts, as well as the self inductance of the loop, are assumed to be negligible. The coefficient of friction between the connector and the bars is equal to 12 and α
(a) Find the steady-state velocity of the connector.
(b) How will your answer differ if the magnetic field was in opposite direction.
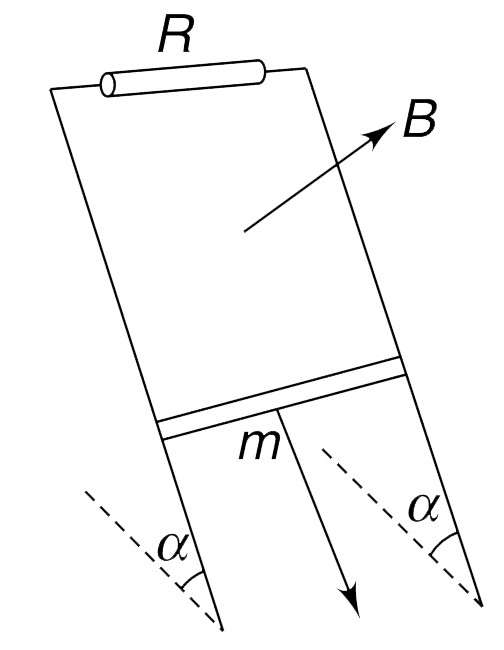
View SolutionA coil of inductance L connects the upper ends of two vertical copper bars separated by a distance l . A horizontal conducting connector of mass m starts falling with zero initial velocity along the bars without losing contact with them. The whole system is located in a uniform magnetic field B perpendicular to the plane of the bars. Find the law of motion x(t) of the connector.

View Solution