A bent rod PQR with PQ=QR=1 shown in figure-5.329 is rotating about its end P with a constant angular speed ω in a region of transverse magnetic field of induction B:

EMF induced across the rod is Bωl2/2
EMF induced across the rod is Bω2l/2
Potential difference between points Q and R on the rod is Bω2/2
Potential difference between points Q and R on the rod is zero
The correct Answer is:A, D
Step by step video, text & image solution for A bent rod PQR with PQ=QR=1 shown in figure-5.329 is rotating about its end P with a constant angular speed omega in a region of transverse magnetic field of induction B: by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTEXERCISE - Numerical MCQs
60 Videos
- CURRENT ELECTRICITYBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - CURRENT ELECTRICITYEXERCISE - All Questions
389 Videos
- ELECTROSTATICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - ELECTROSTATICSEXERCISE - Unsolved Numberical Problems
73 Videos
Similar Questions
A conductor of length T'is rotated about one of its ends at a constant angular speed 'ω' in a plane perpendicular to a uniform magnetic field B. Plot graphs to show variations of the emf induced across the ends of the conductor with (i) angular speed o and (ii) length of the conductor i.
View SolutionA thin rod of mass m and length l is rotated in a horizontal plane about one of its ends with a constant angular speed ω in gravity free space.Then the tension at the midpoint of the rod is 3mlω2p.The value of p is?
View Solution
Knowledge Check
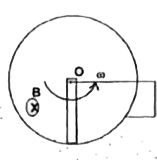
A non-conducting disk of radius R is rotating about its own axis with constant angular velocity ω in a perpendicular uniform magnetic field B as shown in figure. The emf induced between centre and rim of disk is
 ABωR22BBωR2CZeroDBωR23
ABωR22BBωR2CZeroDBωR23A metallic rod of length l is hinged at the point M and is rotating about an axis perpendicular to the plane of paper with a constant angular velocity ω. A uniform magnetic field of intensity B is acting in the region (as shown in the figure) parallel to the plane of paper. The potential difference between the points M and N
 Ais always zeroBvaries between 12Bωl2 to 0Cis always 12Bωl2Dis always Bωl2
Ais always zeroBvaries between 12Bωl2 to 0Cis always 12Bωl2Dis always Bωl2A copper rod AB of length L, pivoted at one end A, rotates at constant angular velocity omega, at right angles to a uniform magnetic field of induction B. The e.m.f developed between the mid point C of the rod and B is
 ABωl24BBωl22C3Bωl24D3Bωl28
ABωl24BBωl22C3Bωl24D3Bωl28
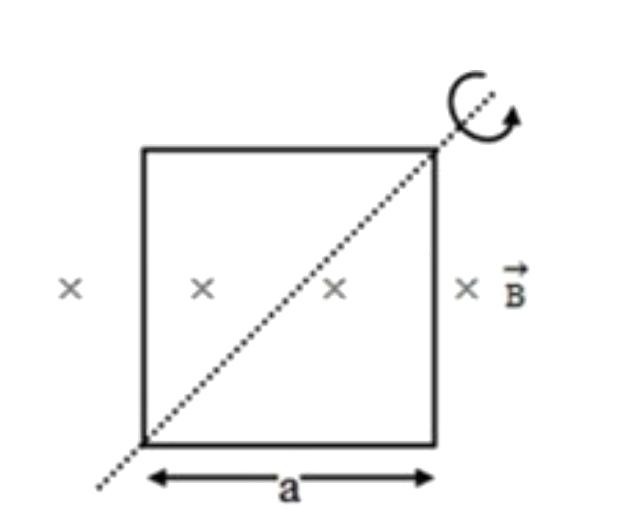
A square loop of side a is rotating about its diagonal with angular velocity ω in a perpendicular magnetic field →B It has 10 turns. The emf induced is
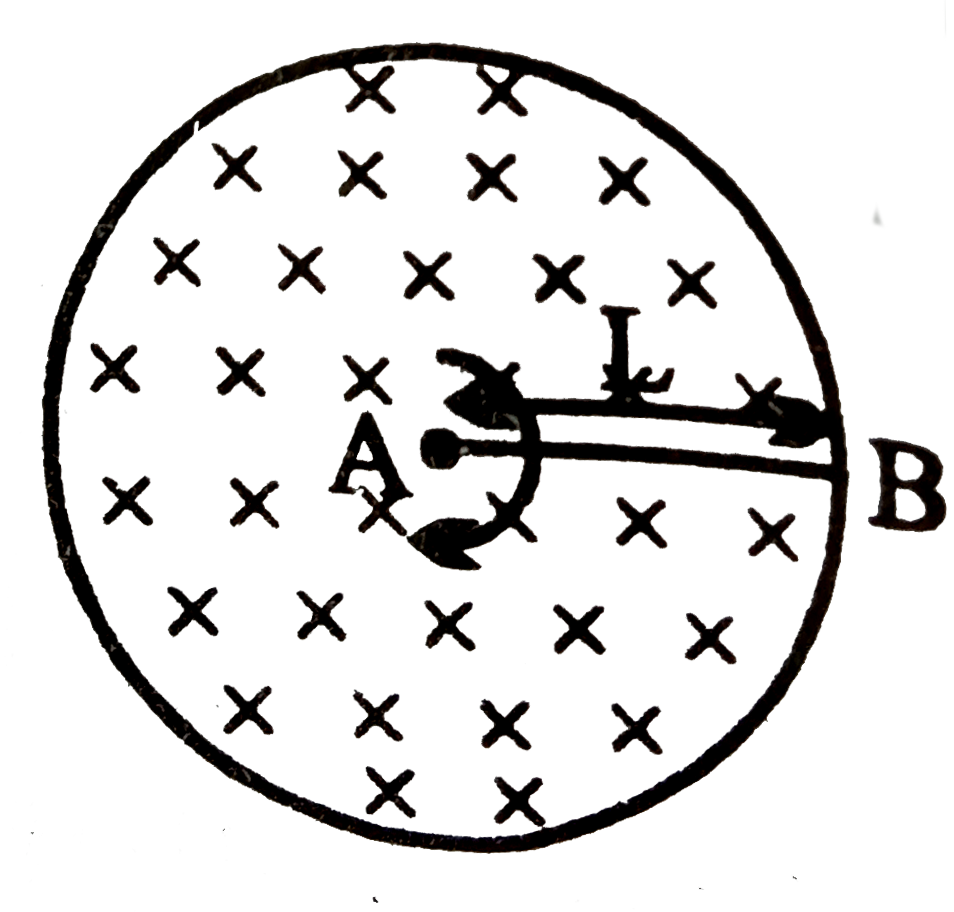
View SolutionIn the figure shown a long conductor carries constant current I. A rod PQ of length l is in the plane of the rod.The rod is rotated about point P with constant angular velocity ω as shown in the figure.Find the e.m.f induced in the rod in the position shown.Indicate which points is at high potential.
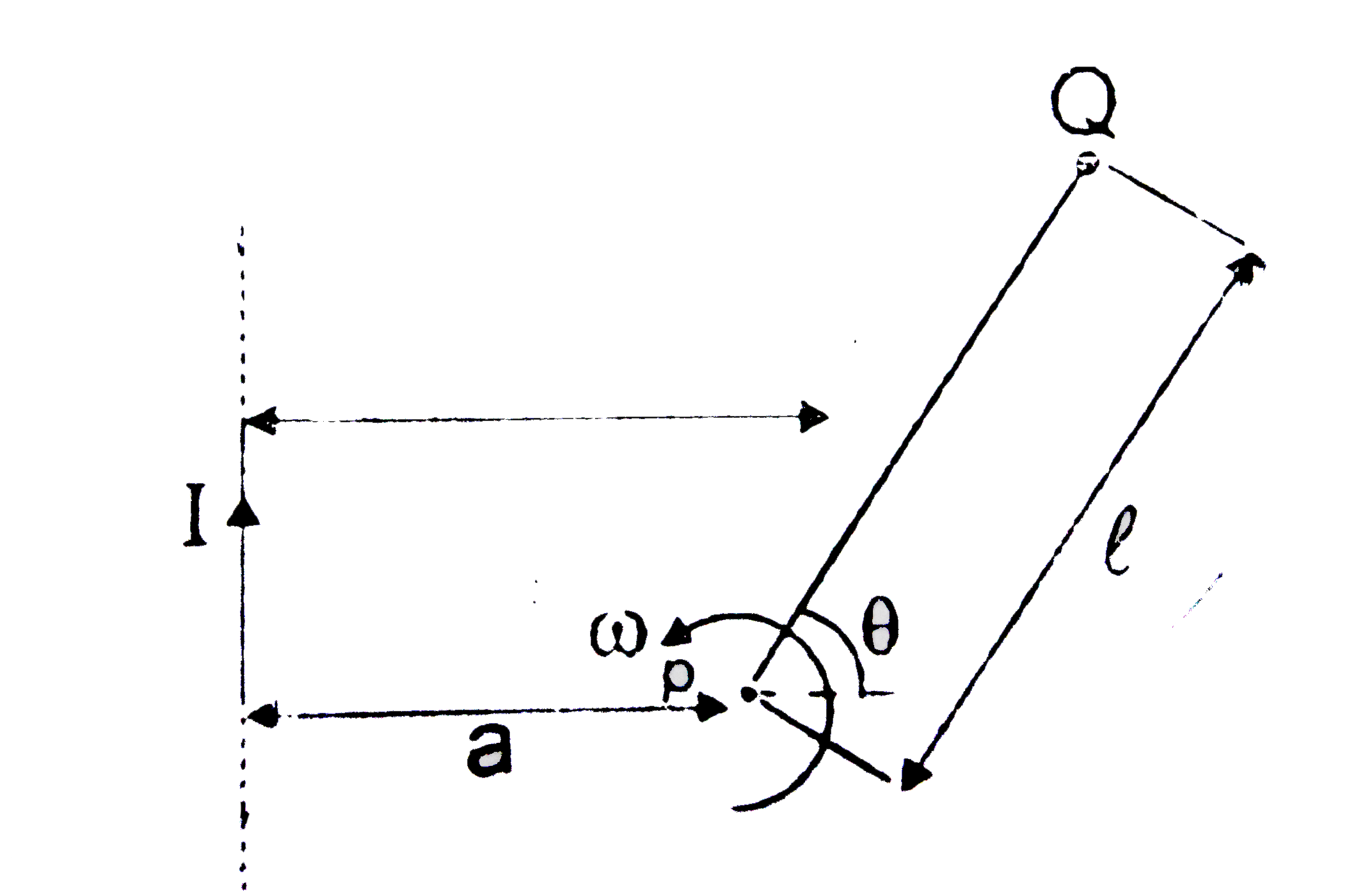
View SolutionA metallic rod of length l & resistance R is free to rotate about one of its ends over a smooth rigid circular metallic frame of radius i in an inward magnetic field of induction B. What torque should be applied by an external angent to rotate the rod with constant angular velocity ω ?
View SolutionA metallic rod of length l is rotated at a constant angular speed ω, normal to a uniform magnetic field B. Derive an expression for the current induced in the rod, if the resistance of the rod is R.
View SolutionA conducting wheel in which there are four rods of lengthe l as shown in figure is rotating with angular velocity ω in a uniform magnetic field B. The induced potential difference between its centre and rim will be

View Solution
