A lit of mass M=0.8 ton is raised to a height h=40m in t=0.5min. The v

Class 12 PHYSICS CURRENT ELECTRICITY

Topper's Solved these Questions

HEATING AND CHEMICAL EFFECT OF CURRENTBOOK - NN GHOSHCHAPTER - HEATING AND CHEMICAL EFFECT OF CURRENTEXERCISE - EXAMPLE B
23 Videos
GAUSS THEOREM AND ITS APPLICATIONBOOK - NN GHOSHCHAPTER - GAUSS THEOREM AND ITS APPLICATIONEXERCISE - EXAMPLES(a)
24 Videos
INTRODUCTION TO MODERN PHYSICSBOOK - NN GHOSHCHAPTER - INTRODUCTION TO MODERN PHYSICSEXERCISE - EXERCISE
21 Videos

Knowledge Check

A transformer of efficiency 90% has turns ratio 10 : 1. If the voltage across the primary is 220 V and current in the primary is 0.5 A, then the current in secondary is
A5.5 A
B $5 A$
C $4 A$
D4.5 A
Figure shows an electrical calorimeter to determine specific heat capacity of an unknown liquid, First of all, the mass of empty calorimeter (a copper container) is measured and suppose it is $m_{1}$ . Then the unknown liquid is poured in it. Now the combined mass of calorimeter+liquid system is measured and let it be $m_{2}$ . So the mass of liquid is $(m_{2} - m_{1})$ . Initially both were at room temperature ( $θ_{0}$ ).
Now a heater is immeresed in if for time interval $t$ . The voltage drop across the heater is $V$ and current passing through it is $I$ . Due to heat supplied, the temperature of both the liquid and calorimeter will rise simultaneously. After $t sec$ , heater was switched off, and final temperature is $θ_{r}$ . If there is no heat loss to surroundings. Heat supplied by the heater=Heat absorbed by the liquid+heat absorbed by the calorimeter $(V I) t = (m_{2} - m_{1}) S_{1} (θ_{f} - θ_{0}) + m_{1} S_{c} (θ_{f} - θ_{0})$
The specific heat of the liquid $S_{1} = \frac{\frac{(V I) t}{θ_{f} - θ_{0}} - m_{1} S_{c}}{(m_{2} - m_{1})}$

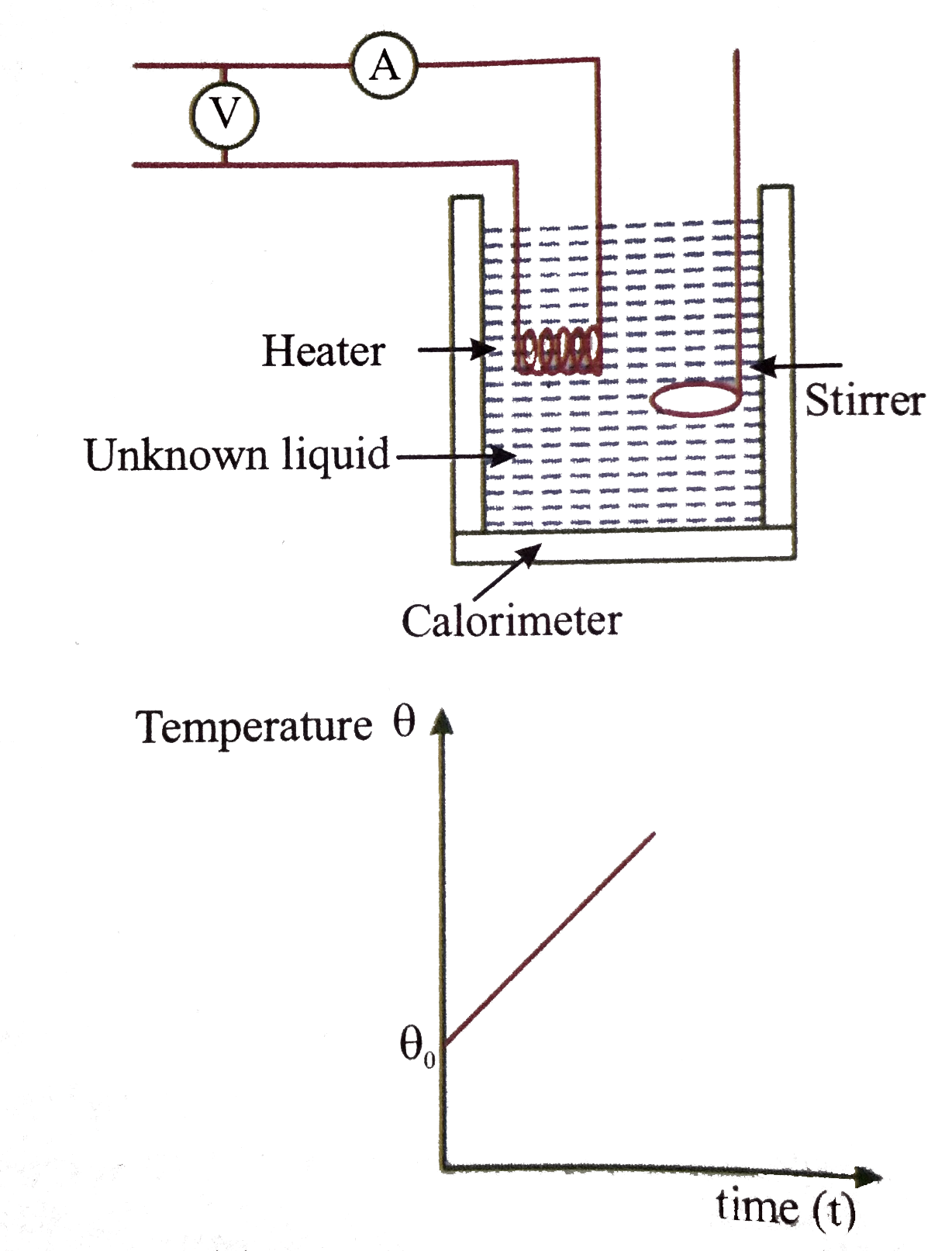
Radiation correction: There can be heat loss to environment. To compensate this loss, a correction is introduced.
Let the heater was on for $t sec$ , and then it is switched off. Now the temperature of the mixture falls due to heat loss to environment. The temperature of the mixture is measured $t / 2 sec$ . after switching off. Let the fall in temperature during this time is $ɛ$
Now the corrected final temperature is taken as $θ_{f} = θ_{f} + ɛ$
In this experiment voltage across the heater is $100.0 V$ and current is $10.0 A$ , and heater was switched on for $t = 700.0 sec$ . Initially all elements were at room temperature $θ_{\circ} = {10.0}^{\circ} C$ and final temperature was measured as $θ_{f} = {73.0}^{\circ} C$ .
Mass of empty calorimeter ws $1.0 k g$ and the combined mass of calorimeter + liquid is $3.0 k g$ . The specific heat capacity of the calorimeter $= 3.0 \times 10^{3} J / k g^{\circ} C$ . The falls in temperature $350$ second after switching off the heater was ${7.0}^{\circ} C$ . Find the specific heat capacity of the unknown liquid in proper significant figures.
A $3.5 \times 10^{3} J / k g^{\circ} C$
B $3.50 \times 10^{3} J / k g^{\circ} C$
C $4.0 \times 10^{3} J / k g^{\circ} C$
D $3.500 \times 10^{3} J / k g^{\circ} C$
Figure shows an electrical calorimeter to determine specific heat capacity of an unknown liquid, First of all, the mass of empty calorimeter (a copper container) is measured and suppose it is $m_{1}$ . Then the unknown liquid is poured in it. Now the combined mass of calorimeter+liquid system is measured and let it be $m_{2}$ . So the mass of liquid is $(m_{2} - m_{1})$ . Initially both were at room temperature ( $θ_{0}$ ).
Now a heater is immeresed in if for time interval $t$ . The voltage drop across the heater is $V$ and current passing through it is $I$ . Due to heat supplied, the temperature of both the liquid and calorimeter will rise simultaneously. After $t sec$ , heater was switched off, and final temperature is $θ_{r}$ . If there is no heat loss to surroundings. Heat supplied by the heater=Heat absorbed by the liquid+heat absorbed by the calorimeter $(V I) t = (m_{2} - m_{1}) S_{1} (θ_{f} - θ_{0}) + m_{1} S_{c} (θ_{f} - θ_{0})$
The specific heat of the liquid $S_{1} = \frac{\frac{(V I) t}{θ_{f} - θ_{0}} - m_{1} S_{c}}{(m_{2} - m_{1})}$

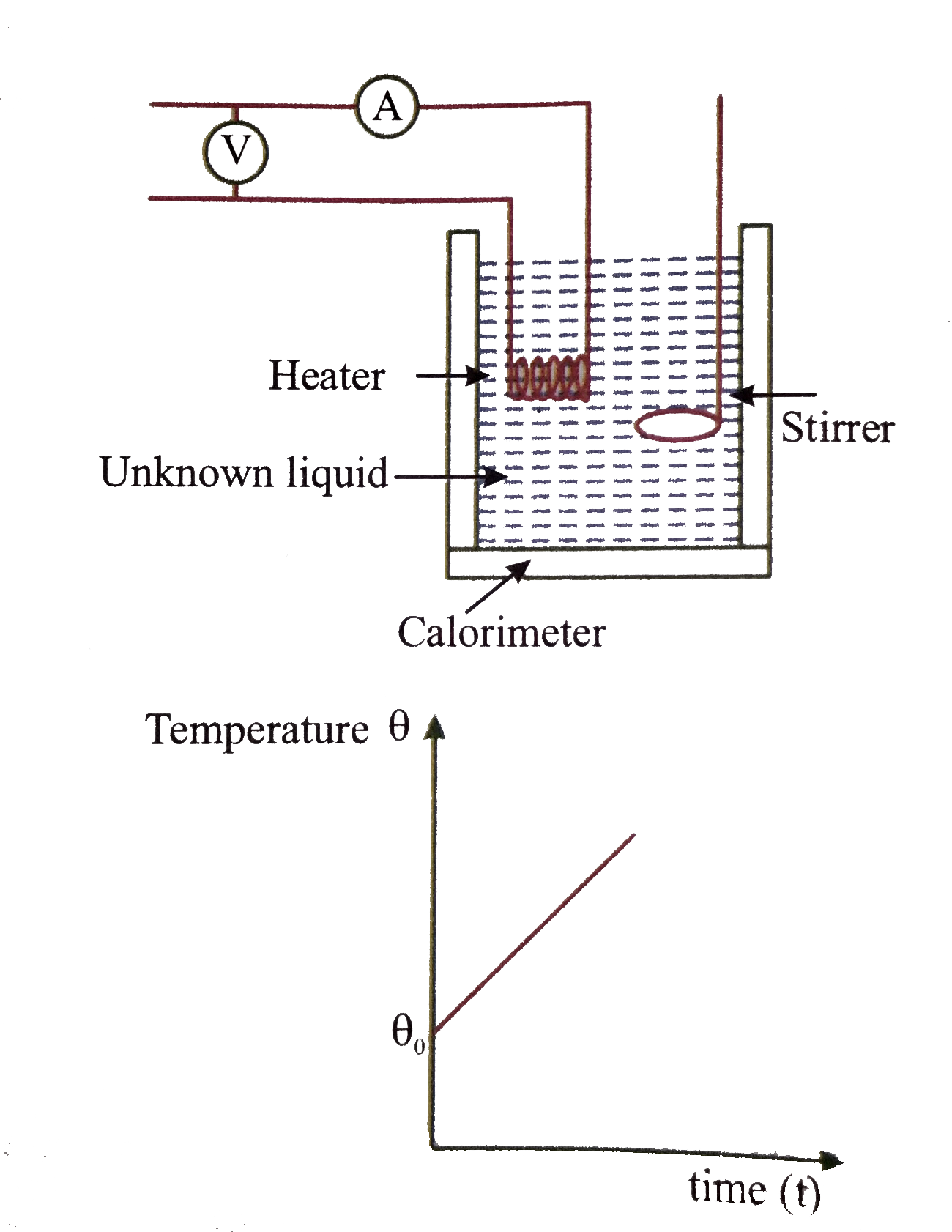
Radiation correction: There can be heat loss to environment. To compensate this loss, a correction is introduced.
Let the heater was on for $t sec$ , and then it is switched off. Now the temperature of the mixture falls due to heat loss to environment. The temperature of the mixture is measured $t / 2 sec$ . after switching off. Let the fall in temperature during this time is $ɛ$
Now the corrected final temperature is taken as $θ_{f} = θ_{f} + ɛ$
If mass and specific heat capacity of calorimeter is negligible, what would be maximum permissible error in $S_{l}$ . Use the date mentioned below.
$m_{1} \to$ , $S_{l} \to 0$ , $m_{2} = 1.00 k g$ ,
$V = 10.0 V$ , $I = 10.0 A$ ,
$t = 1.00 \times 10^{2} sec$ , $θ_{0} = 15^{\circ} C$ ,
Corrected $θ_{1} = 65^{\circ} C$
A $4 %$
B $5 %$
C $8 %$
D $12 %$

A lit of mass M=0.8 ton is raised to a height h=40m in t=0.5min. The voltage across the motar terminals is V=220V and the motar efficiency $η = 90 %$ . Find the power an current consumed by the motar and the price of one hoisting if B.O.T. costs 60 paise.

The correct Answer is:11.6KW, 52.7A, 6paise

Topper's Solved these Questions

Similar Questions

Knowledge Check

A transformer of efficiency 90% has turns ratio 10 : 1. If the voltage across the primary is 220 V and current in the primary is 0.5 A, then the current in secondary is

NN GHOSH-HEATING AND CHEMICAL EFFECT OF CURRENT-EXAMPLE B

A lit of mass M=0.8 ton is raised to a height h=40m in t=0.5min. The voltage across the motar terminals is V=220V and the motar efficiency η = 90 % . Find the power an current consumed by the motar and the price of one hoisting if B.O.T. costs 60 paise.

The correct Answer is:11.6KW, 52.7A, 6paise

Topper's Solved these Questions

Similar Questions

Knowledge Check

A transformer of efficiency 90% has turns ratio 10 : 1. If the voltage across the primary is 220 V and current in the primary is 0.5 A, then the current in secondary is

NN GHOSH-HEATING AND CHEMICAL EFFECT OF CURRENT-EXAMPLE B

A lit of mass M=0.8 ton is raised to a height h=40m in t=0.5min. The voltage across the motar terminals is V=220V and the motar efficiency $η = 90 %$ . Find the power an current consumed by the motar and the price of one hoisting if B.O.T. costs 60 paise.