In a PO box experiment a student obserfes that he does not get the null point for any of the ratios. But when the ratio is he finds that the deflectioin is to the right by 1 division for in the rheostat arm and 0.2 direction to the left when it is . Compute the correct value of the unkown resistance from the observations of the student.
The correct Answer is:5.9683
Step by step video, text & image solution for In a PO box experiment a student obserfes that he does not get the null point for any of the ratios. But when the ratio is 1000:10 he finds that the deflectioin is to the right by 1 division for 596Omega in the rheostat arm and 0.2 direction to the left when it is 597Omega. Compute the correct value of the unkown resistance from the observations of the student. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
In a PO box experiment it is found that for the 1000:10 ratio, the deflection is to the left by 2 divisions when R is 437Ω and to the right by 1.3 cm division when R is 436Ω. Compute the correct value of the unknown resistance.
View SolutionIn A PO box experiment it is found that for the 100:10 ratio deflection in the galvanometer is to the left by 0.7 division of the scale when resistance I the rheostat are is 978Ω and to the right by 1.2 division when is 979Ω. Calculate the unknown resistance.
View Solution
Knowledge Check
In a meter bridge experiment the resistance to be meausred in connected int the right gap and a known resistance in the left gap has value of 50±0.2Ω when the null points is judged to be at 60±2.0 cm. The students notes is judged to be of the bridge wire are not at 0.0 cn and 100.0 cm of the scale makes ends. The value of the unknown resistance should be expressed as
A33.33±1ΩB75±1ΩC75.0±0.9ΩD33.4±0.5ΩIn a meter bridge experiment the resistance of resistance box is 16Ω which is inserted in right gap The null point is obtained at 36cm from the left end the least count of meter scale is lmm What is the value of unknown resistence ?( Error = L.C or L.C /2 )
A9±5128ΩB9±5256ΩC9±5512ΩD1289±12560ΩDirection :
Resistive force proportional to object velocity
At low speeds, the resistive force acting on an object that is moving a viscous medium is effectively modeleld as being proportional to the object velocity. The mathematical representation of the resistive force can be expressed as
R=−bv
Where v is the velocity of the object and b is a positive constant that depends onthe properties of the medium and on the shape and dimensions of the object. The negative sign represents the fact that the resistance froce is opposite to the velocity.
Consider a sphere of mass m released frm rest in a liquid. Assuming that the only forces acting on the spheres are the resistive froce R and the weight mg, we can describe its motion using Newton's second law. though the buoyant force is also acting on the submerged object the force is constant and effect of this force be modeled by changing the apparent weight of the sphere by a constant froce, so we can ignore it here.
Thus mg−bv=mdvdt⇒dvdt=g−bmv
Solving the equation
v=mgb(1−e−bt/m)
where e=2.71 is the base of the natural logarithm
The acceleration becomes zero when the increasing resistive force eventually the weight. At this point, the object reaches its terminals speed v1 and then on it continues to move with zero acceleration
mg−bT=0
⇒mT=mgb
Hence v=vT(1−evtm)
In an experimental set-up four objects I,II,III,IV were released in same liquid. Using the data collected for the subsequent motions value of constant b were calculated. Respective data are shown in table.
ObjectIIIIIIVMass (in kg.)1234Constant bin (N-s)/m3.71.41.42.8
A small sphere of mass 2.00 g is released from rest in a large vessel filled with oil. The sphere approaches a terminal speed of 10.00 cm/s. Time required to achieve speed 6.32 cm/s from start of the motion is (Take g=10.00m/s2) :A5.00×10−3sB1.00×10−2sC2.5×10−3sD1.00×10−3s
In an experiment with post office box, the ratio arms are 1000:10. If the value of third resistance is 870Ω, find the unknown resistance.
View SolutionExperiment set up of a meter bridge .When the two unknown resistance XandY are intserted, the null point D is obtained 40cm from the end A .When a resistance of 30Ω is connected in series with X the mill point shift by 10cm .Find the position of the point when the 30Ω resistance is connected in series with X, the null point shifts by 10 cm. Find the position of the null point when the 30Ω resistance is connected in series with resistance Y instead of X. Determine the values of resistances XandY
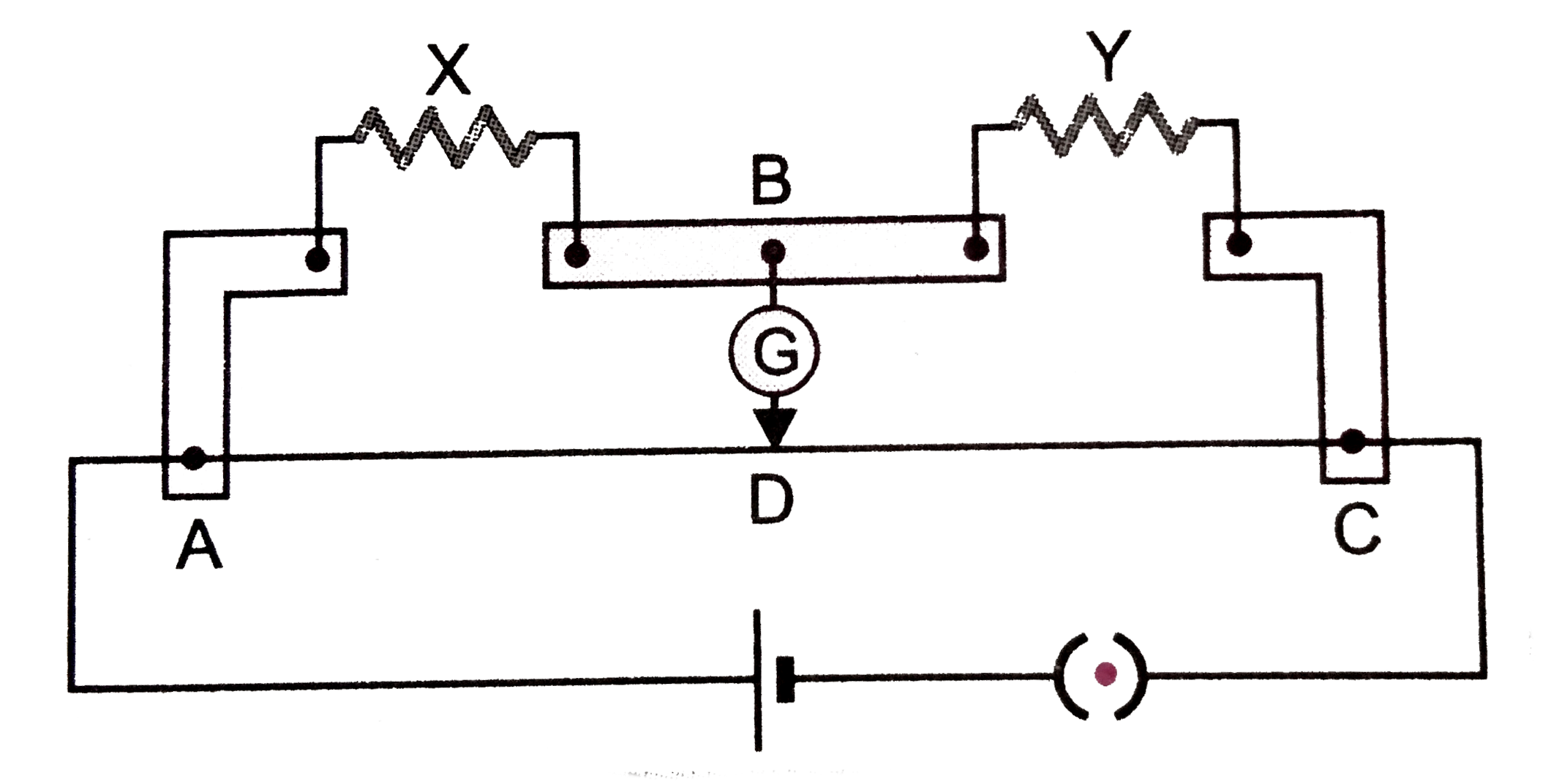
View SolutionAn unknown resistance is connected in a left gap of a metre bridge . The balance point is obtained when a resistance of 10Ω is taken out from the resistance box in the right gap. On increasing the resistance from the resistance box by 12.5Ω the balance point shifts by 20 cm.
find the unknown resistance.
View SolutionWhen the resistance in left and right gap of a mere bridge are 101Ω and 1Ω respectively, the null point is found at 99.5 cm. When the resistances are interchanged the null point is now at 0.7cm. Calcualte the end-corrections of the metre bridge.
View SolutionA rectangular conductor LMNO is placed in a uniform magnetic field of 0.5 T. The field is directed perpendicular to the plane of the conductor. When the arm MN of length of 20 cm is moved towards left with a velocity of 10ms−1, calculate the emf induced in the arm. Given the resistance of the arm to be 5Ω (assuming that other arms are of negligible resistance) find the value of the current in the arm.
View Solution

