A block of mass m is placed on an inclined plane with angle of inclination θ let N, fL and F respectively represent the normal reaction limiting force of frcition and the net force down the inclined plane. Let μ be the coefficient of friction. the variations of N, fL and F with θ is indicated by plotting graphs as shown its figure. Then, curves 1,2 and 3 respectively represent.

N,F and fL
F, fL and F
P,N and fL
fL and F
The correct Answer is:c
Step by step video, text & image solution for A block of mass m is placed on an inclined plane with angle of inclination theta let N, f_(L) and F respectively represent the normal reaction limiting force of frcition and the net force down the inclined plane. Let mu be the coefficient of friction. the variations of N, f_(L) and F with theta is indicated by plotting graphs as shown its figure. Then, curves 1,2 and 3 respectively represent. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Similar Questions
A block of mass m is at rest on a rough inclined plane of angle of inclination θ. If coefficient of friction between the block and the inclined plane is μ, then the minimum value of force along the plane required to move the block on the plane is
View SolutionA block of mass m is placed on a rough inclined plane of inclination θ kept on the floor of the lift. The coefficient of friction between the block and the inclined plane is μ. With what acceleration will the block slide down the inclined plane when the lift falls freely ?
View Solution
Knowledge Check
A block of mass m slides down with uniform speed on an inclined plane having inclination θ If the coefcient of friction between the inclined plane and the block is then the contact force between them is
AmgsinθBmgC√(mgsinθ)2+(μπgcosθ)2Dmgcosθ√1+μ2A block of mass m slides down an inclined plane of inclination θ with uniform speed. The coefficient of friction between the block and the plane is μ. The contact force between the block and the plane is
AmgBmgsinθ√1+μ2CmgsinθD√(mgsinθ)2+(μmgcosθ)2A block of mass m slides down an inclined plane of inclination θ with uniform speed The coefficient of friction between the block and the plane is μ. The contact force between the block and the plane is .
Amgsinθ√1+μ2B√(mgsinθ)2+(μmgcosθ)2CmgsinθDmg
A block of mass m slides down an inclined plane which makes an angle θ with the horizontal. The coefficient of friction between the block and the plane is μ. The force exerted by the block on the plane is
View SolutionA block of mass mm remains stationary on a fixed inclined plane of inclination θ . If μ= coefficient of static friction the reaction of ground on the block is:
View SolutionA horizontal force acting on a block of mass m which is placed on an inclined plane (as shown in the figure). What is the normal reaction N on the block?
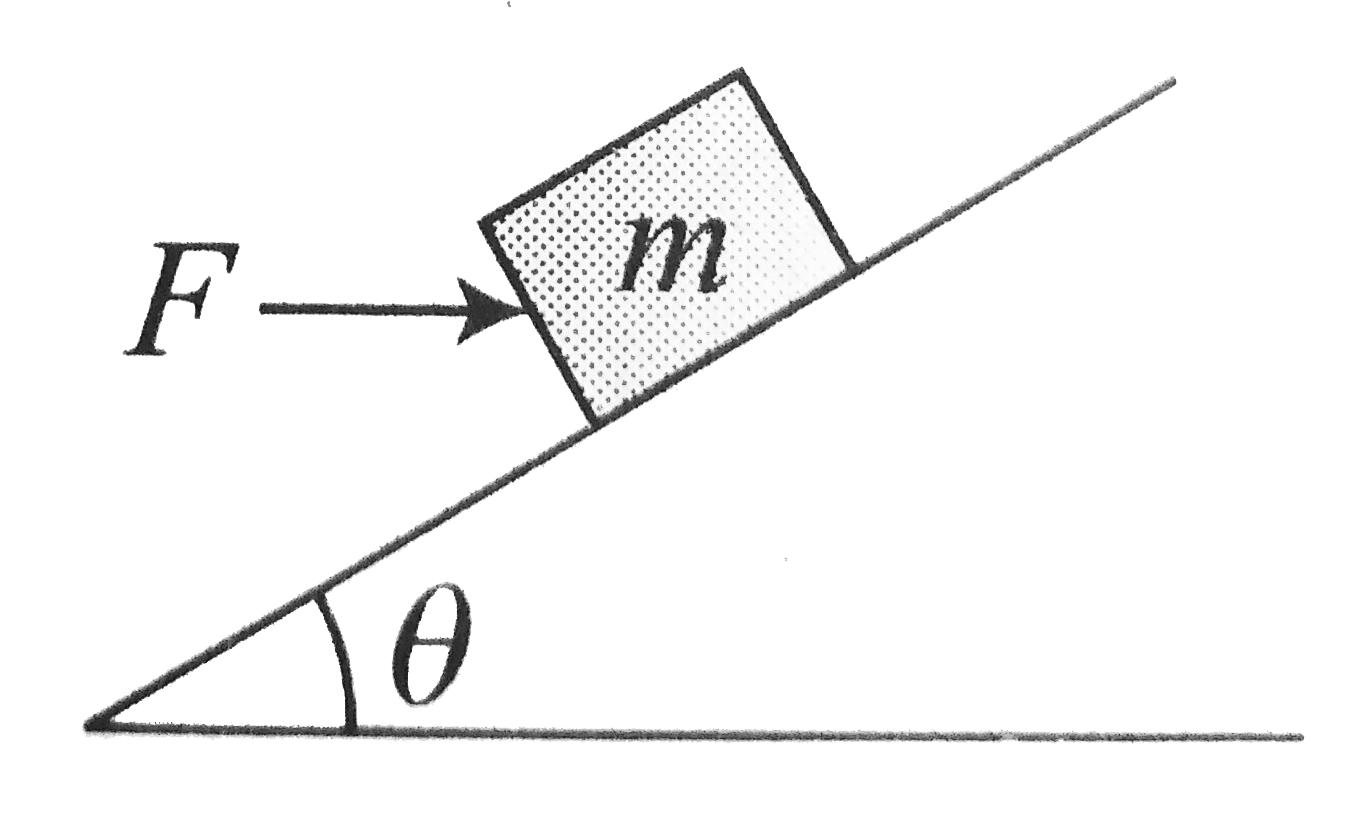
View SolutionA block mass 'm' is placed on a frictionless inclined plane of inclination θ with horizontal. The inclined plane is accelerated horizontally so that the block does not slide down. In this situation vertical force exerted by the inclined plane on the block is:
View SolutionA body is sliding down an inclined plane having coefficient of friction 1/3. If the normal reaction is three times that of the resultant downward force along the inclined plane, the angle between the inclined plane and the horizontal is
View Solution
