A cylinderical jar of cross-sectional area of 50cm2 is filled with water to a height of 20cm. It carries a tight fitting piston of negligible mass. Calculate the pressure at the bottom of the jar when a mass of 1kg is placed on the piston . Ignore atmospheric pressure.
The correct Answer is:(3920Nm−2)
To solve the problem, we need to calculate the pressure at the bottom of the cylindrical jar when a mass of 1 kg is placed on the piston. We will follow these steps:
Step 1: Calculate the force exerted by the piston
The force exerted by the piston can be calculated using the formula:
F=m⋅g
Where:
- m=1kg (mass placed on the piston)
- g=9.8m/s2 (acceleration due to gravity)
Calculating the force:
F=1kg⋅9.8m/s2=9.8N
Step 2: Calculate the area of the piston in square meters
The area of the piston is given as 50cm2. We need to convert this to square meters:
A=50cm2=50×10−4m2=0.005m2
Step 3: Calculate the pressure due to the piston
Pressure is defined as force per unit area:
Ppiston=FA
Substituting the values:
Ppiston=9.8N0.005m2=1960Pa
Step 4: Calculate the pressure due to the water column
The pressure due to the water column can be calculated using the formula:
Pwater=ρ⋅g⋅h
Where:
- ρ=1000kg/m3 (density of water)
- g=9.8m/s2 (acceleration due to gravity)
- h=20cm=0.2m (height of the water column)
Calculating the pressure:
Pwater=1000kg/m3⋅9.8m/s2⋅0.2m=1960Pa
Step 5: Calculate the total pressure at the bottom of the jar
The total pressure at the bottom of the jar is the sum of the pressure due to the piston and the pressure due to the water column:
Ptotal=Ppiston+Pwater
Substituting the values:
Ptotal=1960Pa+1960Pa=3920Pa
Final Answer
The pressure at the bottom of the jar when a mass of 1 kg is placed on the piston is:
Ptotal=3920Pa
---
The force exerted by the piston can be calculated using the formula:
F=m⋅g
Where:
- m=1kg (mass placed on the piston)
- g=9.8m/s2 (acceleration due to gravity)
F=1kg⋅9.8m/s2=9.8N
The area of the piston is given as 50cm2. We need to convert this to square meters:
A=50cm2=50×10−4m2=0.005m2
Pressure is defined as force per unit area:
Ppiston=FA
Substituting the values:
Ppiston=9.8N0.005m2=1960Pa
The pressure due to the water column can be calculated using the formula:
Pwater=ρ⋅g⋅h
Where:
- ρ=1000kg/m3 (density of water)
- g=9.8m/s2 (acceleration due to gravity)
- h=20cm=0.2m (height of the water column)
Pwater=1000kg/m3⋅9.8m/s2⋅0.2m=1960Pa
The total pressure at the bottom of the jar is the sum of the pressure due to the piston and the pressure due to the water column:
Ptotal=Ppiston+Pwater
Substituting the values:
Ptotal=1960Pa+1960Pa=3920Pa
The pressure at the bottom of the jar when a mass of 1 kg is placed on the piston is:
Ptotal=3920Pa
Topper's Solved these Questions
Similar Questions
A cylindrical tube of cross sectional area 20cm2 is filled with water to a height of 10cm. The tube carries a tight fitting piston of negligible mass. What will be the pressure exerted at the bottom of the tube when a mass of 2 kg placed on the piston? Atmospheric pressure can be ignored.
View SolutionA rigid cylindrical container having a cross sectional area of 0.2m2 is filled with water up to a height of 5.0m. There is a piston of negligible mass over the water. Piston can slide inside the container without friction. When a weight of 2000kg is placed over the piston, it moves down by 0.25 mm compressing the water.
ρ= Density of water =103kg/m2,Patm= Atmospheric pressure =105N/m2 and g=10m/s2. With this information calculate the speed of sound in water.

View Solution
Knowledge Check

A cylindrical tube of uniform cross-sectional area A is fitted with two air tight frictionless pistons. The pistons are connected to each other by a metallic wire. Initially the pressure of the gas is P0 and temperature is T0, atmospheric pressure is also P0. Now the temperature of the gas is increased to 2T0, the tension in the wire will beA2P0ABP0ACP0A2D4P0AA cylindrical tube of uniform cross-sectional area A is fitted with two air tight frictionless postion.
 The pistons are connected to each other by a metallic wirte. Initially the pressure of the gas is po and temperature is To, atmospheric pressure is also po Now the temperature of the gas is increased to 2T0, the tension in the wire will be A2poABpoACpoA2DpoA
The pistons are connected to each other by a metallic wirte. Initially the pressure of the gas is po and temperature is To, atmospheric pressure is also po Now the temperature of the gas is increased to 2T0, the tension in the wire will be A2poABpoACpoA2DpoAA cyclinderical vessel of cross-sectional area 1000cm2, fitted with a frictonless piston of mass 10kg, and filled with water completely. A small hole of cross-sectional area 10mm2 is opened at a point 50cm deep from the lower surface of the piston. The velocity of efflux from the hole will be
A10.5m/sB3.4m/sC0.8m/sD0.2m/s
_S01_053_Q01.png)
A large cylinderical tank of cross-sectional area 1m2 is filled with water . It has a small hole at a height of 1 m from the bottom. A movable piston of mass 5 kg is fitted on the top of the tank such that it can slide in the tank freely. A load of 45 kg is applied on the top of water by piston, as shown in figure. The value of v when piston is 7 m above the bottom is (g=10m/s2)
(a). √120m/s
(b). 10m/s
(c). 1m/s
(d). 11m/s
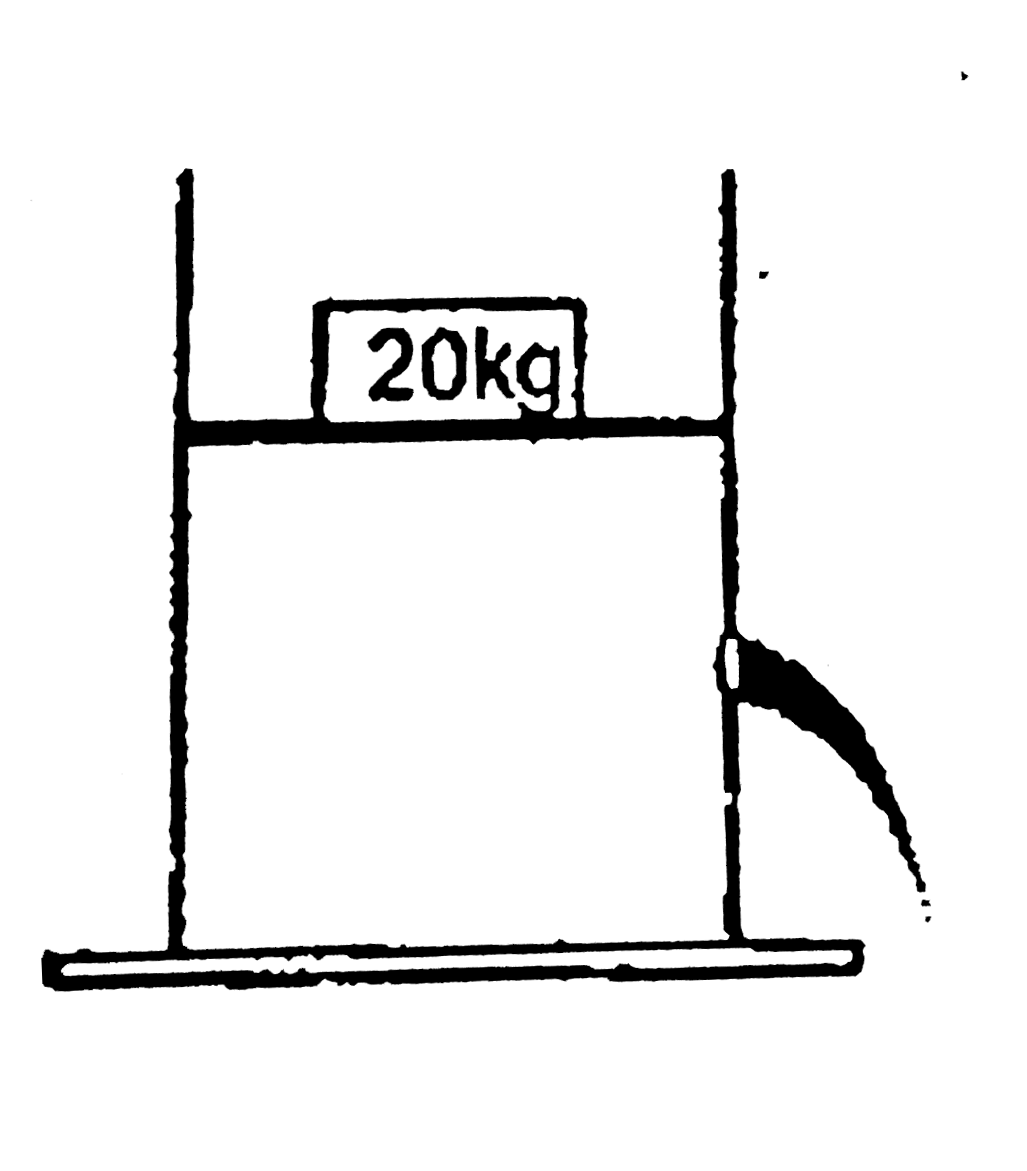
View SolutionA long cylindrical tank of cross-sectional area 0.5m2 is filled with water. It has a small hole at a height 50cm from the bottom. A movable piston of cross-sectional area almost equal to 0.5m2 is fitted on the top of the tank such that it can slide in the tank freely. A load of 20kg is applied on the top of the water by piston, as shown in the figure. Calculate the speed of the water jet with which it hits the surface when piston is 1m above the bottom. (Ignore the mass of the piston)

View SolutionA long cylindrical tank of cross-section area 0.5m2 is filled with water. It has an opening at a height 50 cm from the bottom, having area of cross-section 1×10−4m2. A movable piston of cross-section area almost equal to 0.5m2 is fitted on the top of the tank such that it can slide in the tank freely. A load of 20 kg is applied on the top of the water by piston, as shown in the figure. Find the speed of the water jet with which it hits the surface when piston is 1m above the bottom. (Ignore the mass of the piston). If this speed is (18x) m/s, find the value of x.
View SolutionA piston of cross-sectional area 100cm2 is used in a hydraulic pressure to exert a force of 107 dyne on the water. The cross-sectional area of the other piston which support a truck of mass 2000 kg is
View SolutionAs shown , a piston chamber pf cross section area A is filled with ideal gas. A sealed piston of mass m is right at the middle height of the cylinder at equilibrium. The friction force between the chamber wall and the piston can be ignored . The mass of the rest of the chamber is M.The atmosphere pressure is P0. Now slowly pull the piston upwards , find the maximum value of M such that the chamber can be lifted off the ground. The temperature remains unchanged.
_E01_049_Q01.png)
View Solution

