Stoke’s law states that the viscous drag force F experienced by a sphere of radius a, moving with a speed V through a fluid with coefficient of viscosity η, is given by F=6πnav. If this fluid is flowing through a cylindrical pipe of radius r, length l and a pressure difference of P across its two ends, then the volume of water V which flows through the pipe in time t can be written as cVt=k(Pl)ηbrc , where k is a dimensional constant. Correct values of a, b and c are
a = 1, b = –1, c = 4
a = –1, b = 1, c = 4
a = 2, b =–1, c = 3
a = 1, b =–2,c=–4
The correct Answer is:A
Step by step video, text & image solution for Stoke’s law states that the viscous drag force F experienced by a sphere of radius a, moving with a speed V through a fluid with coefficient of viscosity eta, is given by F = 6pi"na"v. If this fluid is flowing through a cylindrical pipe of radius r, length l and a pressure difference of P across its two ends, then the volume of water V which flows through the pipe in time t can be written as c(V)/(t)=k((P)/(l))eta^(b)r^(c) , where k is a dimensional constant. Correct values of a, b and c are by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
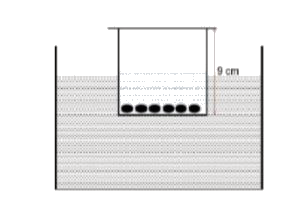
A wide bottom cylindrical massless plastic container of height 9 cm has 40 identical coins inside it and is floating on water with 3 cm inside the water. If we start putting more of such coins on its lid. It is observed that after N coins are put, its equilibrium changes from stable to unstable. Equilibrium in floating is stable if the geometric center of the submerged portion is above the center of mass of the object) The value of N is closed to
View SolutionUsing the method of dimensions, derive an expression for rate of flow (v) of a liquied through a pipe of radius (r ) under a pressure gradient (P/I) Given that V also depends on coefficient of viscosity (η) of the liquied.
View SolutionA liquid of coefficient of viscosity η is flowing steadily through a capillary tube of radius r and length I. If V is volume of liquid flowing per sec. the pressure difference P at the end of tube is given by
View SolutionAn incompressible fluid flows steadily through a cylindrical pipe which has radius 2 R at point A and radius R at point B farther along the flow direction. If the velocity at point A is v, its velocity at point B is
View SolutionThe rate of flow Q (volume of liquid flowing per unit time) through a pipe depends on radius r , length L of pipe, pressure difference p across the ends of pipe and coefficient of viscosity of liquid eta as Q prop r^(a) p^(b) eta^(c ) L^(d) , then
View SolutionWhat flows through a horizontal pipe of radius r at a speed V. if the radius of the pipe is doubled, the speed of flow of water under similar conditions is
View SolutionAn ideal fluid flows through a pipe of circular cross section of radius r at a speed v0. Now a viscous liquid is made to flow through the pipe at the same volume flow rate (measured in m3s–1). Find the maximum speed of a fluid particle in the pipe.
View SolutionA dimensionally consistent relation for the volume V of a liquid of coefficiet of viscosity eta flowing per second through a tube of radius r and length l and having a pressure difference p across its end, is
View SolutionStoke's law states that the viscous drag force F experienced by a sphere of radius a, moving with a speed v through a fluid with coefficient of viscosity η, is given by F=6πη If this fluid is flowing through a cylindrical pipe of radius r, length l and a pressure difference of P across its two ends, then the volume of water V which flows through the pipe in time t can be written as
Vt=K(pl)aηbrc
where k is a dimensionless constant. Correct values of a, b and c are -
View Solutionएक असंपीडय द्रव एक बेलनाकार पाइप में से लगातार बहता है जिसकी बिंदु A पर त्रिज्या 2R है तथा बहने की दिशा में आगे बिंदु B पर त्रिज्या R है । यदि इस द्रव का बिंदु A पर वेग v है, तो बिंदु B पर इसका वेग होगा :
View Solutionजब एक गोलाकार वस्तु किसी द्रव में चलती है तो द्रव उसपर गति की विपरीत दिशा में एक बल लगता है। इस बल का परिमाण F, द्रव का श्यानता गुणांक (coefficient of viscosity) η, गोले की त्रिज्या r तथा गोले के वेग v पर निर्भर करता है। विमाओं की सहायता से F के लिए η, v तथा r में सूत्र प्राप्त करे।
View SolutionF=6πηrv, जहाँ F श्यान बल, η श्यानता गुणांक, r त्रिज्या तथा v वेग है|
View Solutionत्रिज्या r व लम्बाई l की नली के सिरों पर दाबांतर P है। यदि नली से प्रवाहित द्रव की प्रवाह दर v=πQPr4ηl हो, जहाँ η श्यानता गुणांक है, तो Q का मान होगा
View SolutionWater flows through a pipe that is divided into two different areas A and 2A. The pressure at the thin end is p and the velocity of the fluid is v, then the pressure and velocity at the thick end will be
View SolutionAn incompressible fluid flows steadily through a cylindrical pipe which has radius 2 R at point A and radius R at point B farther along the flow direction. If the velocity at point A is v, its velocity at point B is
View Solution

