If, in a ΔABC,a=6cm,b=8cm,c=10cm,
then : sin2A =
625
825
1025
2425
The correct Answer is:D
To find the value of sin2A in triangle ABC where a=6cm, b=8cm, and c=10cm, we can follow these steps:
Step 1: Use the formula for sin2A
We know that:
sin2A=2sinAcosA
So, we need to find sinA and cosA.
Step 2: Use the Cosine Rule to find cosA
The Cosine Rule states:
cosA=b2+c2−a22bc
Substituting the values:
cosA=82+102−622⋅8⋅10
Calculating the squares:
cosA=64+100−36160=128160
Now simplify:
cosA=6480=3240=45
Step 3: Use the Pythagorean identity to find sinA
We know:
sin2A+cos2A=1
Substituting cosA:
sin2A+(45)2=1
Calculating (45)2:
sin2A+1625=1
Subtracting 1625 from both sides:
sin2A=1−1625=2525−1625=925
Taking the square root:
sinA=35
Step 4: Substitute sinA and cosA into the formula for sin2A
Now we can find sin2A:
sin2A=2sinAcosA=2⋅35⋅45
Calculating this:
sin2A=2⋅1225=2425
Final Answer
Thus, the value of sin2A is:
sin2A=2425
We know that:
sin2A=2sinAcosA
So, we need to find sinA and cosA.
The Cosine Rule states:
cosA=b2+c2−a22bc
Substituting the values:
cosA=82+102−622⋅8⋅10
Calculating the squares:
cosA=64+100−36160=128160
Now simplify:
cosA=6480=3240=45
We know:
sin2A+cos2A=1
Substituting cosA:
sin2A+(45)2=1
Calculating (45)2:
sin2A+1625=1
Subtracting 1625 from both sides:
sin2A=1−1625=2525−1625=925
Taking the square root:
sinA=35
Now we can find sin2A:
sin2A=2sinAcosA=2⋅35⋅45
Calculating this:
sin2A=2⋅1225=2425
Thus, the value of sin2A is:
sin2A=2425
Topper's Solved these Questions
- TRIGONOMETRIC FUNCTIONSBook:MARVEL PUBLICATIONChapter:TRIGONOMETRIC FUNCTIONSExercise:MULTIPLE CHOICE QUESTIONS - PART-B: MASTERING THE BEST
Explore 27 Videos
- TRIGONOMETRIC FUNCTIONSBook:MARVEL PUBLICATIONChapter:TRIGONOMETRIC FUNCTIONSExercise:MASTERING THE BEST - ALL TOPICS
Explore 128 Videos
- TRIGONOMETRIC FUNCTIONSBook:MARVEL PUBLICATIONChapter:TRIGONOMETRIC FUNCTIONSExercise:MULTIPLE CHOICE QUESTIONS - PART - A : BUILDING-UP THE BASE (B) Properties of triangles
Explore 27 Videos
- THREE DIMENSIONAL GEOMETRYBook:MARVEL PUBLICATIONChapter:THREE DIMENSIONAL GEOMETRYExercise:MULTIPLE CHOICE QUESTIONS
Explore 39 Videos
- VECTORSBook:MARVEL PUBLICATIONChapter:VECTORSExercise:TEST YOUR GRASP
Explore 20 Videos
Similar Questions
Knowledge Check
If in a ΔABC,a=6cm,b=8cmandc=10cm, then the value of sin 2A is
A6/25B8/25C10/25D24/25In ΔABC, if : a = 2 cm , b = 3cm and c = 4cm, then ∠A =
Acos−1(124)Bcos−1(1116)Ccos−1(78)Dcos−1(−14)In Δ ABC, AB = 6 cms, BC = 10 cms, AC = 8cm and ADI_BC. Find the value of the ratio of BD:DC.
A3:4B9:16C4:5D16:25
In a ΔABC,AB=5,AC=6cm,BC=8cm . Find the length of median AD.
View SolutionA circle in inscribed in a ΔABC having sides 8 cm , 10 cm and 12 cm in Fig Find AD, BE and CF.
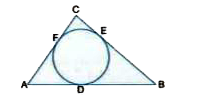
View SolutionIf in ΔABC,b=3cm,c=4cm and the length of the perpendicular from A to the side BC is 2 cm, then how many such triangle are possible ?
View SolutionΔABC~ΔLMN. In ΔABC,AB=5.5cm, BC = 6 cm, CA = 4.5 cm. If MN = 4.8 cm then construct ΔABC and ΔLMN
View SolutionIn ΔABC,AB=4cm,AC=5cmandBC=6cm In ΔPQR,PR=4cm,PQ=5cmandRQ=6cm.ΔABC is congruent to
View Solution