For three events A,B,C the probability that only A occur is (A) P(A) (B) P(A∪B∪C) (C) P(A'∩B'∩C') (D) P(A∩B'∩C')
P(A)
P(A/B∩C)
P(A'∩B∩C)
P(A∩B'∩C')
The correct Answer is:D
Step by step video, text & image solution for For three events A,B,C the probability that only A occur is (A) P(A) (B) P(AuuBuuC) (C) P(Aprime nn B prime nn C prime) (D) P(A nn B prime nn C prime) by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PROBABILITYBook:MARVEL PUBLICATIONChapter:PROBABILITYExercise:MULTIPLE CHOICE QUESTIONS
Explore 239 Videos
- CIRCLE AND CONICS Book:MARVEL PUBLICATIONChapter:CIRCLE AND CONICS Exercise:MISCELLANEOUS MCQs
Explore 50 Videos
- PROBABILITY DISTRIBUTIONSBook:MARVEL PUBLICATIONChapter:PROBABILITY DISTRIBUTIONSExercise:MCQs
Explore 51 Videos
Similar Questions
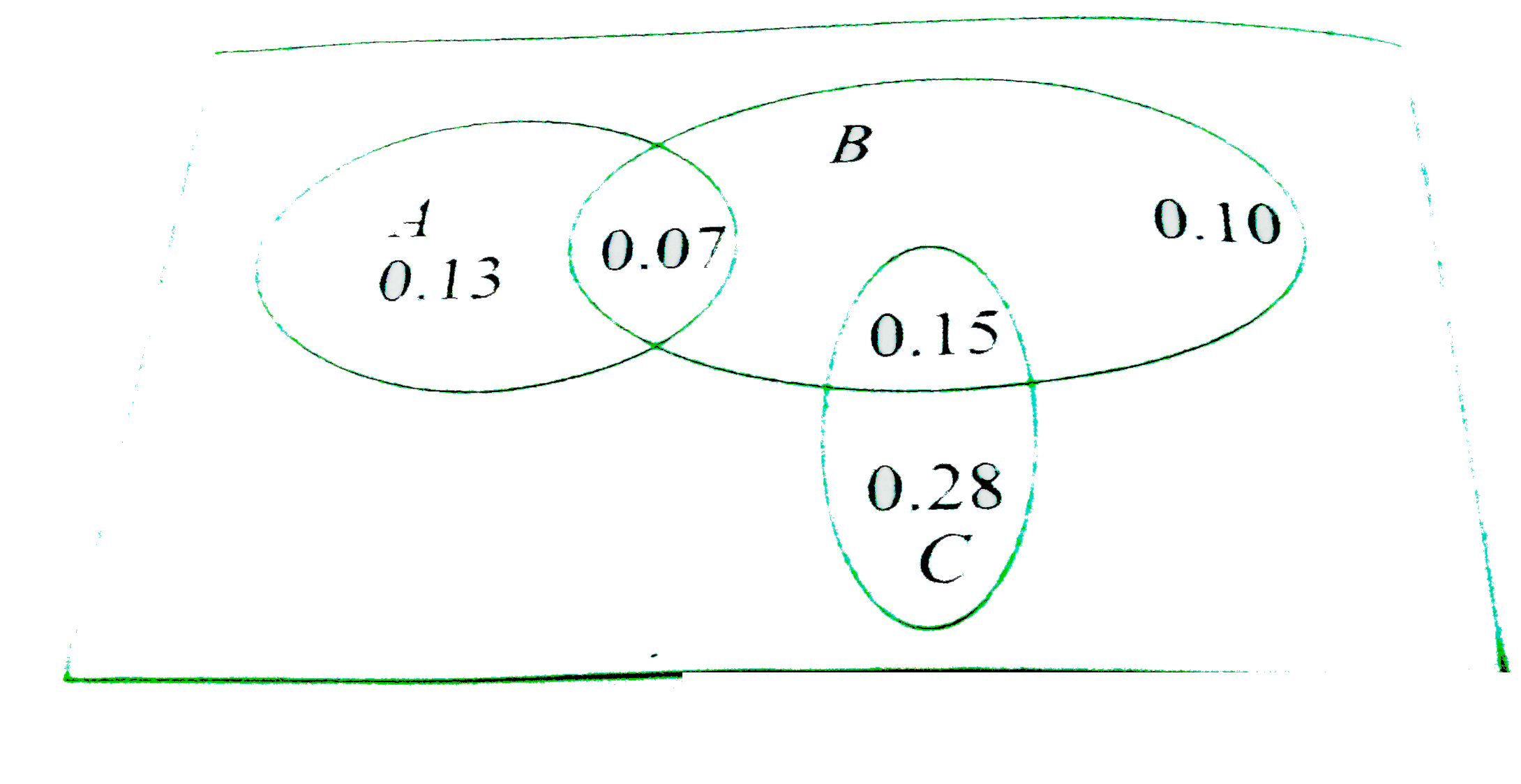
The following Venn diagram shows three events, A, B, and C, and also the probabilities of the various intersections.
Determine
(a) P(A)
(b) P(B∩¯¯¯C)
(c ) P(A∪B)
(d) P(A∩¯¯¯B)
(e) P(B∩C)
(f) Probability of the event that exactly one of A, B, and C occurs.
View SolutionFor any three events A, B and C, prove that, P(A∪B∪C)=P(A)+P(B)+P(C)−P(A∩B)−P(B∩C)−P(C∩A)+P(A∩B∩C) .
View Solution
Knowledge Check
For two given events A and B P(A∩B)=
ANot less than P(A) + P(B) -1BNot greater than P(A) + P(B)CEqual to P(A)+P(B)−P(A∪B)DAll of the above
If AandB are mutually exclusive events such that P(A)=0.35andP(B)=0.45 , find P(A∪B) (ii) P(A∩B) (iii) P(A∩B′) (iv) P(A′∩B′)
View SolutionA∪(B∩C) is equal to :
a) (A∪B)∩(A∪C)
b) (A∩B)∪(A∩C)
C) A∪(B∪C)
d) none of these
View SolutionThere are three events A, B, C such that n(B)=230,n(¯¯¯A∩B∩¯¯¯C)=100,n(A∩B∩¯¯¯C)=50 and n(A∩B∩C)=10, then value of n(A∩B∩C) is
View SolutionIf P is a probability function, show that for any two events A, B. P(A∩B)≤P(A)≤P(A∪B)≤P(A)+P(B)
View SolutionThe set (A∪B∪C)∩(A∩B'∪C')'∩C' is equal to
View SolutionThe probabilities of three events A,B,C are such that P(A)=0.3,P(B)=0.4,P(C)=0.8,P(A∩B)=0.09,P(A∩C)=0.28,P(A∩B∩C)0.08andP(A∪B∪C)≤0.75.Show that P(B∩C) lies in the interval [0.21,0.46].
View SolutionIf A and B are two sets then A∩(B−C)=(A∩B)−(A∩C)
View Solution

