Points A,B ,C , D on y2=4ax have parameters t1,t2,t3,t4 respectively . If AB∣∣CD , then
t1+t3=t2+t4
t1+t2=t3+t4
t1−t3=t2−t4
t1+t4=t2−t3
The correct Answer is:B
Step by step video, text & image solution for Points A,B ,C , D on y^(2) = 4ax have parameters t_(1) , t_(2), t_(3), t_(4) respectively . If AB || CD , then by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CIRCLE AND CONICS Book:MARVEL PUBLICATIONChapter:CIRCLE AND CONICS Exercise:MISCELLANEOUS MCQs
Explore 50 Videos
- CIRCLE AND CONICS Book:MARVEL PUBLICATIONChapter:CIRCLE AND CONICS Exercise:MISCELLANEOUS MCQs
Explore 50 Videos
- BERNOULLI TRIALS AND BINOMIAL DISTRIBUTIONBook:MARVEL PUBLICATIONChapter:BERNOULLI TRIALS AND BINOMIAL DISTRIBUTIONExercise:MULTIPLE CHOICE QUESTIONS
Explore 79 Videos
- PROBABILITYBook:MARVEL PUBLICATIONChapter:PROBABILITYExercise:MULTIPLE CHOICE QUESTIONS
Explore 239 Videos
Similar Questions
Normals are drawn to the parabola y2=4ax at the points A, B, C whose parameters are t1,t2andt3, respectively. If these normals enclose a triangle PQR, then prove that its area is a22(t−t2)(t2−t3)(t3−t1)(t1+t2+t3)2 Also prove that ΔPQR=ΔABC(t1+t2+t3)2.
View SolutionP and Q are two distinct points on the parabola, y2=4x with parameters t and t1 respectively. If the normal at P passes through Q, then the minimum value of t21 is
View Solution
Knowledge Check
Points A,B,C,D, on y2=4ax have parameters t1,t2,t3,t4 respectively . If AB ⊥ CD then (t1+t2)(t3+t4)=
A0B1C-4D4A circle drawn on any focal AB of the parabola y2=4ax as diameter cute the parabola again at C and D. If the parameters of the points A, B, C, D be t1,t2,t3 and t4 respectively, then the value of t3,t4, is
A-1B2C3Dnone of theseIf a circle cuts a rectangular hyperbola xy=1 in four points P,Q,R,S and the parameters of these four points be t1,t2,t3andt4 respectively and −20t1t2t3t4=k, then value of k equals
A1B−1C−4Dnone
The chord AC of the parabola y2=4ax subtends an angle of 90∘ at points B and D on the parabola. If points A, B, C and D are represented by (at2i,2ati),i=1,2,3,4 respectively, then find the value of ∣∣∣t2+t4t1+t3∣∣∣.
View SolutionThe chord AC of the parabola y2=4ax subtends an angle of 90∘ at points B and D on the parabola. If points A, B, C and D are represented by (at2i,2ati),i=1,2,3,4 respectively, then find the value of ∣∣∣t2+t4t1+t3∣∣∣.
View SolutionTwo identical rods AB and CD, each of length L are connected as shown in figure-4.22. Their cross-sectional area is A and their thermal conductivity is k. Ends A, C and D are maintained at temperatures T1,T2andT3 respectively. Neglecting heat loss to the surroundings, find the temperature at B.
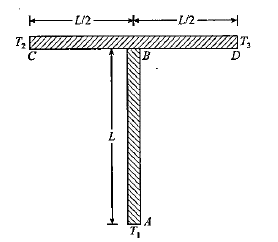
View SolutionA variable chord PQ of the parabola y2=4ax is drawn parallel to the line y = x if the parameter of the points P and Q on the parabola be t1andt2 respectively and then prove that t1+t2=2. Also show that the locus of the point of intersection of the normals at P and Q is 2x - y = 12a.
View SolutionA circle drawn on any focal AB of the parabola y2=4ax as diameter cute the parabola again at C and D. If the parameters of the points A, B, C, D be t1,t2,t3 and t4 respectively, then the value of t3,t4, is
View Solution

