A rod 0.5 m long has two masses each of 20 gram stuck at its ends. If the masses are treated as point masses and if the mass of the rod is neglected, then the moment of inertia of the system about a transverse axis passing through the centre is
1.25×10−3kg−m2
2.5×10−3kg−m2
4××10−3kg−m2
5×10−3kg−m2
The correct Answer is:B
I=Σmr2=2m1r21=2[20×10−3×0.25×0.25]
=2.5×10−3 kg-m2
Topper's Solved these Questions
Similar Questions
Two masses m1andm2 are placed at a distance r from each other. Find out the moment of inertia of system about an axis passing through their centre of mass.
View SolutionTwo point masses m1 and m2 are joined by a weightless rod of length r. Calculate the moment of inerrtia of the system about an axis passing through its centre of mass and perpendicular to the rod.
View Solution
Knowledge Check
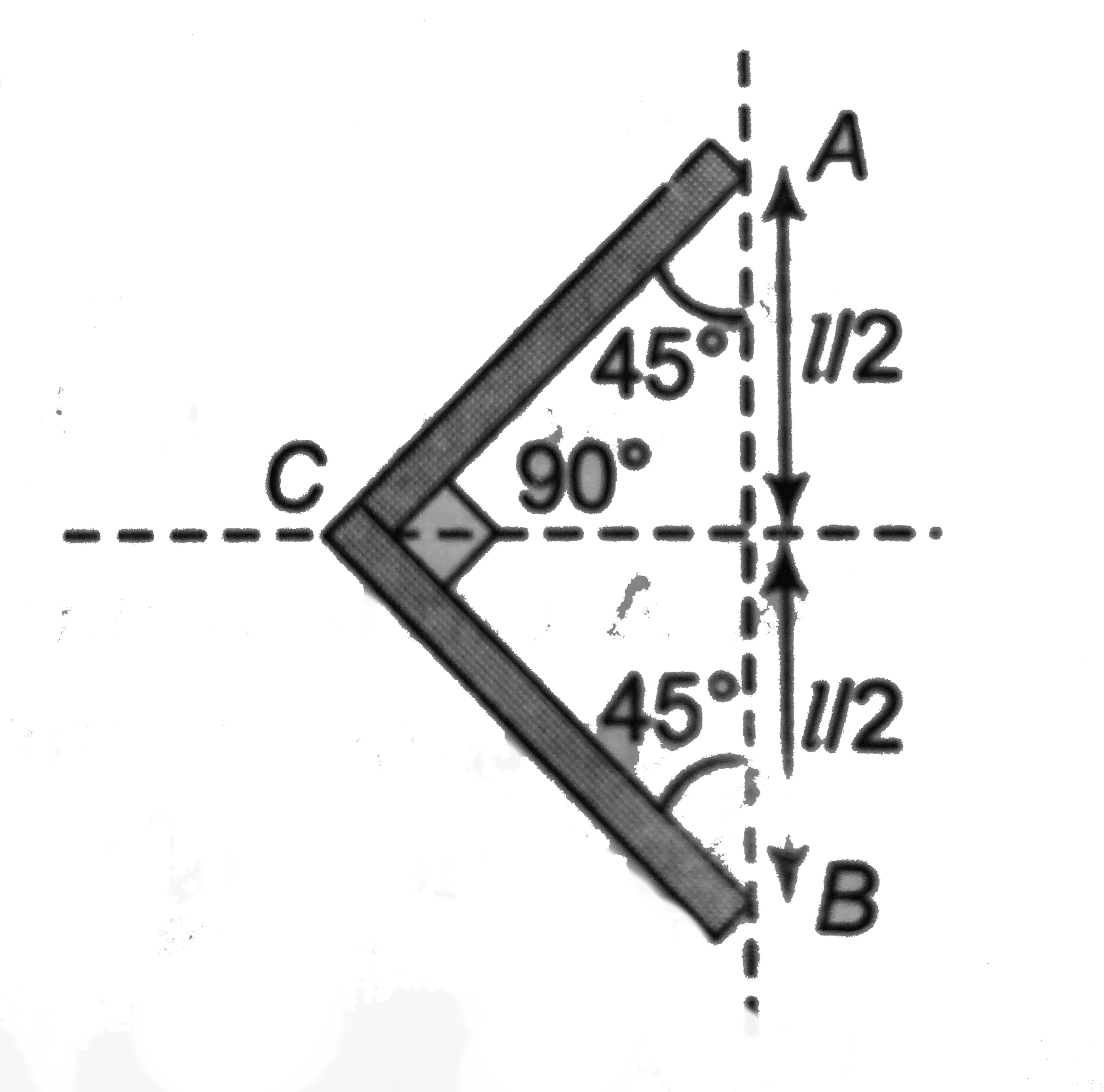
Linear mass density of the two rods system, AC and CD is x. moment of inertia of two rods about an axis passing through AB isAxl34√3Bxl3√2Cxl34Dxl36√2A light rod of length l has two masses m1 and m2 attached to its two ends. The moment of inertia of the system about an axis perpendicular to the rod and passing through the centre of mass is.
A(m1+m2)l2B√m1m2l2Cm1m2m1+m2l2Dm1+m2m1m2l2A light rod of length l has two masses m1 and m2 attached to its two ends. The moment of inertia of the system about an axis perpendicular to the rod and passing through the centre of mass is.
A(m1+m2)l2B√m1m2l2Cm1m2m1+m2l2Dm1+m2m1m2l2
Four masses m, 2 m, 3 m and 4 m are connected by a rod of negligible mass. The moment of inertia of the system about the axis AB is
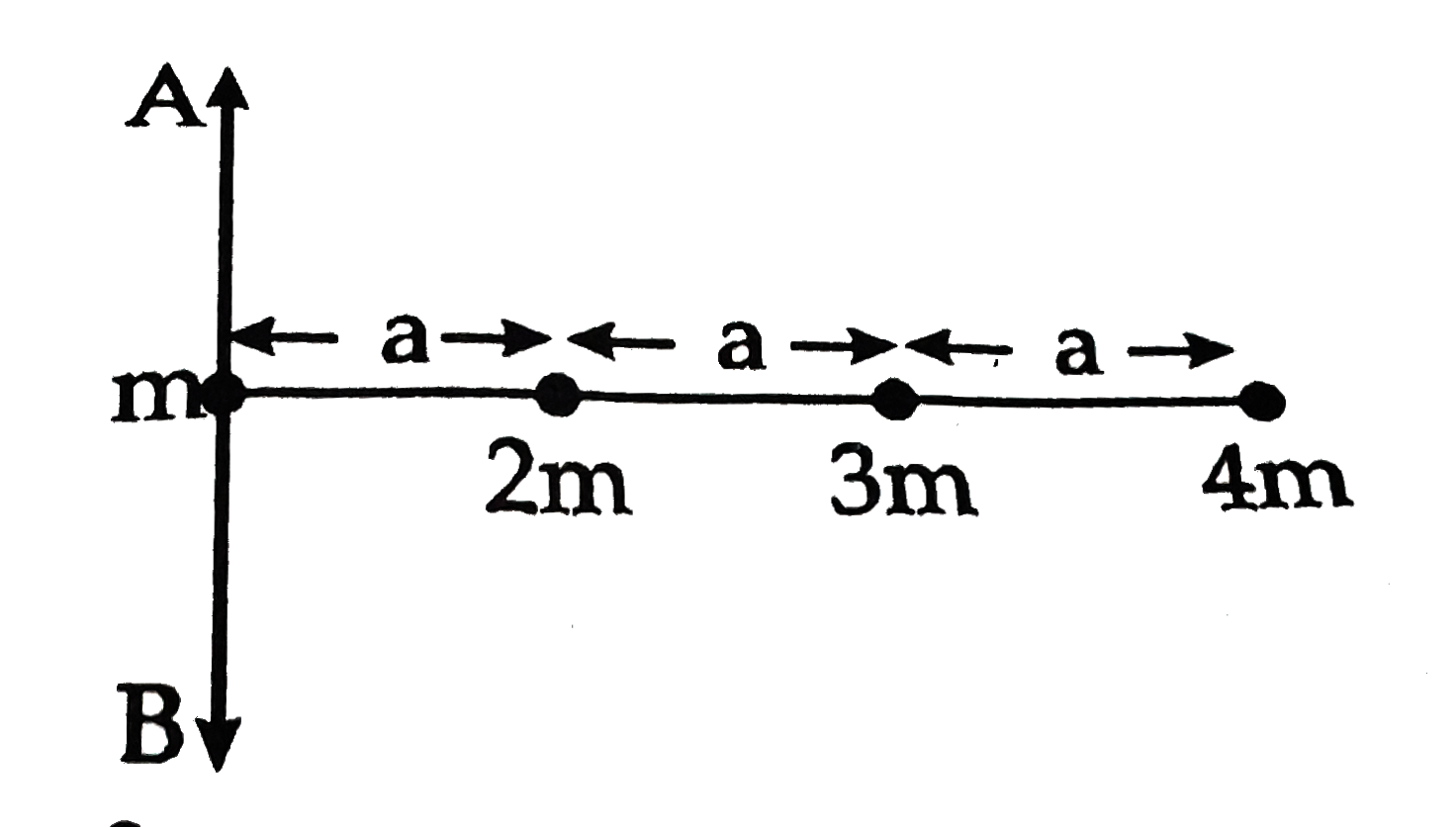
View SolutionTwo point masses m and 4m are connected by a light rigid rod of length l at the opposite ends. Moment of inertia of the system about an axis perpendicular to the length and passing through the centre of mass is
View SolutionTwo spheres each of mass M and radius R/2 are connected with a massless rod of length R. Find the moment of inertia of the system about an axis passing through the centre of one of the sphere and perpendicular to the rod
View SolutionA light rod of length l has two masses m1 and m2 attached to its two ends . The moment of inertia of the system about an axis perpendicular to the rod and passing through the centre of mass is
View SolutionTwo spheres each mass M and radius R are connected with massless rod of length 2R . Then moment of inertia of the system about an axis passing through the centre of one of sphere and perpendicular to the rod will be
View Solution
