The speed of sound in a liquid is .The density of the liquid is .Determine the bulk modulus of elasticity of the liquid.
The correct Answer is:
To determine the bulk modulus of elasticity of the liquid, we can use the relationship between the speed of sound in a medium, its density, and its bulk modulus. The formula is given by:
v=√Bρ
where:
- v is the speed of sound in the medium,
- B is the bulk modulus of elasticity,
- ρ is the density of the medium.
Step 1: Write down the known values
- Speed of sound, v=1500m/s
- Density of the liquid, ρ=1.0×103kg/m3
Step 2: Rearrange the formula to solve for bulk modulus B
To find B, we can rearrange the formula:
B=v2⋅ρ
Step 3: Substitute the known values into the equation
Now, substitute the values of v and ρ:
B=(1500m/s)2⋅(1.0×103kg/m3)
Step 4: Calculate (1500m/s)2
Calculate the square of the speed of sound:
(1500)2=2250000m2/s2
Step 5: Multiply by the density
Now, multiply this result by the density:
B=2250000⋅(1.0×103)=2250000000N/m2
Step 6: Express in scientific notation
Convert this result into scientific notation:
B=2.25×109N/m2
Final Answer
The bulk modulus of elasticity of the liquid is:
B=2.25×109N/m2
---
- v is the speed of sound in the medium,
- B is the bulk modulus of elasticity,
- ρ is the density of the medium.
- Speed of sound, v=1500m/s
- Density of the liquid, ρ=1.0×103kg/m3
To find B, we can rearrange the formula:
Now, substitute the values of v and ρ:
Calculate the square of the speed of sound:
Now, multiply this result by the density:
Convert this result into scientific notation:
The bulk modulus of elasticity of the liquid is:
Topper's Solved these Questions
Similar Questions
The speed of sound in a liquid of density 2×103kg/m3 is 1000 m/s. Determine the bulk modulus of elasticity of the liquid.
View SolutionIn taking a solid ball of rubber from the surface to the bottom of a lake of 180m depth, reduction in the volume of the ball is 0.01%. The density of water of the lake is 1×103kg/m3. Determine the value of the bulk modulus of elasticity of rubber . (g=9.8m/s2)
View Solution
Knowledge Check
When a block of volume 1.00×10−3m3 is hung from a spring scale as shown in Fig. (a) the scale reads 10.0 N . When the same block is then placed in an unknown liquid , it floats with two -third of its volume submerged as suggested in Fig. (b) . The density of water is 1.00×10−3kg/m3
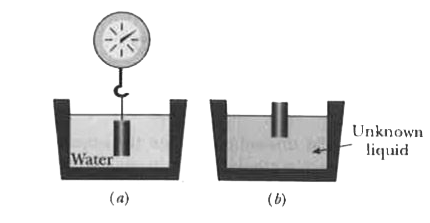
Determine the density of the unknown liquid .A3.03×103kg/m3B4.62×103kg/m3C6.16×103kg/m3D8.01×103kg/m3A solid cylinder of length l , cross sectional area A and density 54×103kgm−3 is immersed such that it floats with its axis vertical at the liquid - liquid interface with length l/4 in the denser liquid as shown in the figure . The lesser dense liquid is open to atmospheric pressure P0. If the density of lesser dense liquid is 1.0×103 kg m−3 then the density of denser liquid will be
 A1.5×103kg m−3B2.0×103kg m−3C2.5×103kg m−3D3.0×103kg m−3
A1.5×103kg m−3B2.0×103kg m−3C2.5×103kg m−3D3.0×103kg m−3The velocity of sound in alcohol is 1300 m/s and the density of alcohol is 0.08 g/cm3. The bulk modulus of alcohol is
A0.65×10−3N/M2B1.35×103N/m2C0.65×106N/m2D1.35×108N/m2
Find the intensity of sound wave whose frequency is 250 Hz. The displacement amplitude of particles of the medium at this position is 1×10−8 m. The density of the medium is 1kg/m3, bulk modulus of elasticity of the medium is 400N/m2.
View SolutionA liquid rises to a height of 7.0 cm in a capillary tube of radius 0.1 mm. The density of the liquid is 0.8×103kgm−3.If the angle of contact between the liquid and the surface of the tube zero , calculate the surface tension of the liquid Given g=10ms−2.
View SolutionThe sound velocity in a duralumin rod is 5.1×103m/s while the density of the material is 2.7×103kg/m3. Find the Young modulus.
View SolutionSpeed of sound in mercury at a certain temperature is 1450 m/s . Given the density of mercury as 13.6×103kg/m, the bulk modulus for mercury is
View SolutionAn air bubble of radius 1 cm rises with terminal velocity 0.21 cm/s in liquid column. If the density of liquid is 1.47×103kg/m3. Then the value of coefficient of viscosity of liquid ignoring the density of air, will be
View Solution

