The time taken by a simple pendulum to perform 100 vibration is 8 minutes 9 sec in bombay and 8 minutes 20 sec. in pune. Calcualte the ratio of acceleration due to gravity in bombay and pune.
The correct Answer is:1.0455
Step by step video, text & image solution for The time taken by a simple pendulum to perform 100 vibration is 8 minutes 9 sec in bombay and 8 minutes 20 sec. in pune. Calcualte the ratio of acceleration due to gravity in bombay and pune. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Related Playlists
- BOOK - SL ARORACHAPTER - OSCILLATIONSEXERCISE - Exercise233videos
OSCILLATIONS
- BOOK - SL ARORACHAPTER - OSCILLATIONSEXERCISE - Problem23videos
OSCILLATIONS
- BOOK - SL ARORACHAPTER - MOTION IN ONE DIMENSIONEXERCISE - problems for self practice66videos
MOTION IN ONE DIMENSION
- BOOK - SL ARORACHAPTER - Physical worldEXERCISE - Exercise49videos
Physical world
Similar Questions
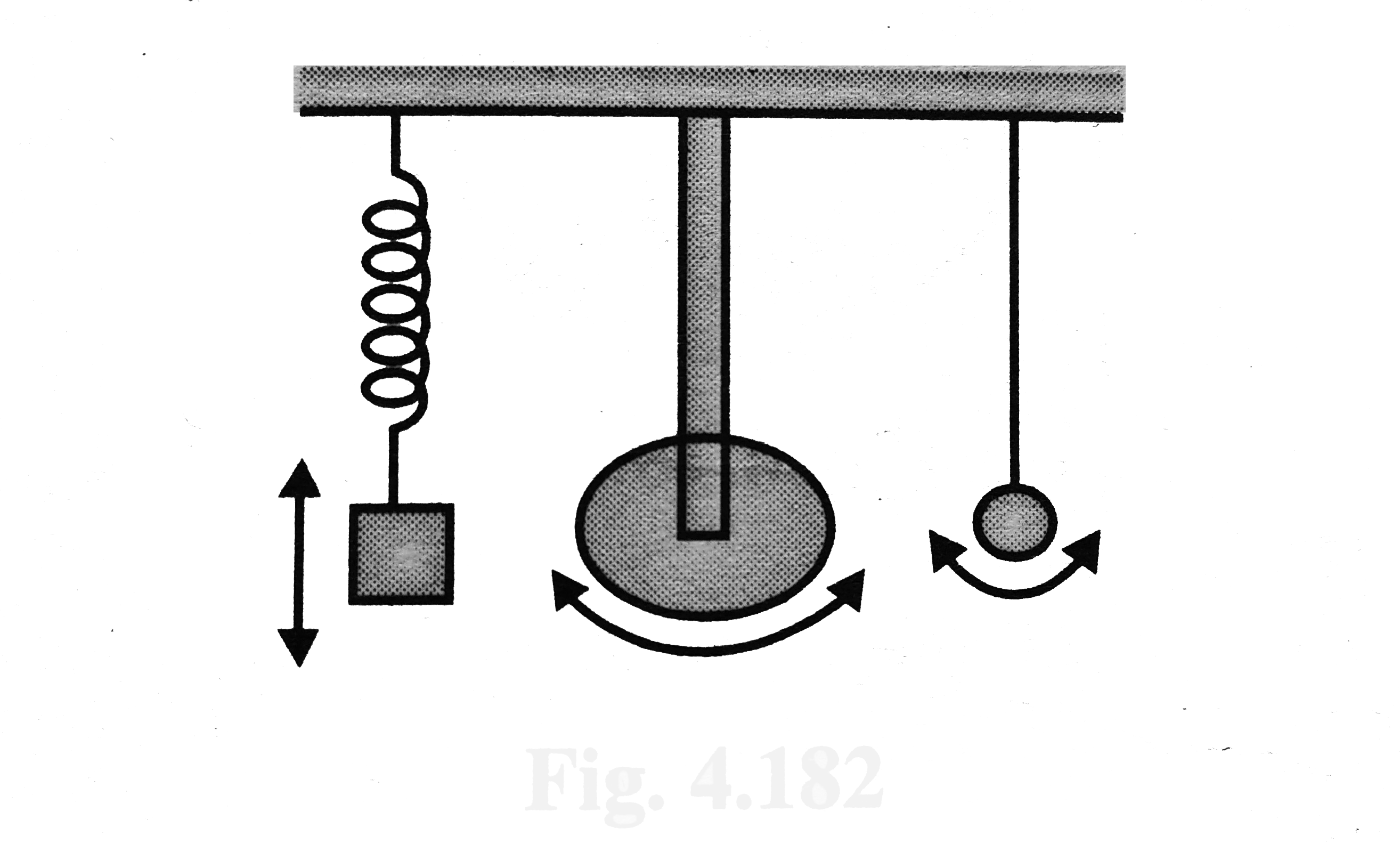
Q. Statement I Three pendulums are suspended from ceiling as shown in Fig. These three pendulums are set to oscillate as shon by arrows, and it is found that all three have same time period. Noe, all three are taken to a place where acceleration due to gravity changes to 4/9th of its value at the first place. If spring pendulum makes 60 cycles in a given time at this place, then torsion pendulum and simple pendulum will also make 60 oscillation in same (given) time interval. Statement II: Time period of torsion pendulum is independent of acceleration due to gravity.View SolutionThe acceleration due to gravity on the surface of earth is 9.8ms−2.Time period of a simple pendulum on earth and moon are 3.5 second and 8.4 second respectively. Find the acceleration due to gravity on the moon .
Hint :Te=2π√LgeTm=2π√Lgm
T2eT2m=gmge
gm=T2eT2mgeView SolutionA simple pendulum undergoes 20 oscillation's in 30 seconds. What is the percentage error in the value of acceleration due to gravity provided length of pendulum is 55cm, least count of rmeasurement of time and length are 1s and 1mm respectively
View SolutionA simple pendulum makes 20 oscillations in one second on the surface of the earth. Determine the time period of the simple pendulum on the surface of a planet where the acceleration due to gravity is one fourth of the acceleration due to gravity on the surface of the earth .
View SolutionA simple pendulum makes 20 oscillations in one second on the surface of the earth. Determine the time period of the simple pendulum on the surface of a planet where the acceleration due to gravity is one fourth of the acceleration due to gravity on the surface of the earth .
View SolutionThe time period of a pendulum on the surfacce of the moon is 5s. If it is a seconds pendulum on earth and the acceleratio due to gravity on the earth is 9.8ms−2, find the acceleration due to gravity on the surface of the moon.
View SolutionIf the length of a seconds pendulum on a planet is 2 m then the acceleration due to gravity on the surface of that planet is ______ (Take the acceleration due to gravity on the surface of the Earth =9.8 ms−2)
View SolutionThe time periods of two simple pendula having different length is the same on two different planets .if the lengths of the two pendula are in ratio of 1:9, then the ratio of the accelerations due to gravity on the two planets is ______
View SolutionGiven that the mass of the earth is 81.5 times the mass of the moon and the diameter of the moon is 0.27 times that of the earth . Calculate the value of acceleration due to gravity at the surface of the moon . Given 'g' on the earth = 9.8ms−2
View SolutionAn artificial satellite is revolving in a circular orbit at a height of 600 km from the earth's surface. If its time of revolution be 100 minutes, calculate the acceleration due to gravity acting on it towards the earth. Radius of earth =6.4×106 m
View Solution


