From what height must a block of ice be dropped in order that it may melt completely. It is assumed that the whole of energy is retained by ice. Given that latent heat of ice =80calg−1.
The correct Answer is:34.29km
To determine the height from which a block of ice must be dropped in order to melt completely, we can use the principle of conservation of energy. The potential energy lost by the ice block when it falls will be equal to the heat energy required to melt the ice.
1. Identify the Variables:
- Let m be the mass of the ice block (in grams).
- The latent heat of fusion of ice, L=80cal/g.
- The acceleration due to gravity, g=9.8m/s2.
2. Calculate the Heat Required to Melt the Ice:
The heat required to melt the ice can be calculated using the formula:
Q=m⋅L
where Q is the heat energy required.
3. Calculate the Potential Energy:
The potential energy (PE) of the ice block at height h is given by:
PE=m⋅g⋅h
4. Set the Potential Energy Equal to the Heat Required:
According to the conservation of energy, the potential energy lost by the ice block will be equal to the heat energy required to melt it:
m⋅g⋅h=m⋅L
5. Cancel the Mass m:
Since m appears on both sides of the equation, we can cancel it out (assuming m≠0):
g⋅h=L
6. Solve for Height h:
Rearranging the equation to solve for h:
h=Lg
7. Substitute the Values:
Now substitute the values of L and g:
h=80cal/g9.8m/s2
8. Convert Calories to Joules (if necessary):
Since 1cal=4.184J, we can convert the latent heat into joules:
L=80cal/g×4.184J/cal=334.72J/g
Thus,
h=334.72J/g9.8m/s2
9. Calculate the Height:
h≈334.729.8≈34.14m
Final Answer:
The block of ice must be dropped from a height of approximately 34.14 meters to melt completely.
- Let m be the mass of the ice block (in grams).
- The latent heat of fusion of ice, L=80cal/g.
- The acceleration due to gravity, g=9.8m/s2.
The heat required to melt the ice can be calculated using the formula:
Q=m⋅L
where Q is the heat energy required.
The potential energy (PE) of the ice block at height h is given by:
PE=m⋅g⋅h
According to the conservation of energy, the potential energy lost by the ice block will be equal to the heat energy required to melt it:
m⋅g⋅h=m⋅L
Since m appears on both sides of the equation, we can cancel it out (assuming m≠0):
g⋅h=L
Rearranging the equation to solve for h:
h=Lg
Now substitute the values of L and g:
h=80cal/g9.8m/s2
Since 1cal=4.184J, we can convert the latent heat into joules:
L=80cal/g×4.184J/cal=334.72J/g
Thus,
h=334.72J/g9.8m/s2
h≈334.729.8≈34.14m
The block of ice must be dropped from a height of approximately 34.14 meters to melt completely.
Topper's Solved these Questions
Similar Questions
From what height must a block of ice fall to just melt by the impact assuming that half of the heat generated is absorbed by ice? (J=4.2 joules per calories and L=80 kilocalories per kg)
View SolutionCalculate change in entropy when 5g of pure ice melts to form water at 0∘C Given latent heat of ice is 80cal/g at 0∘C.
View Solution
Knowledge Check
From what minimum height a block of ice has to be dropped in order that 0.5% of ice melts on hitting the ground ?
A171.43mB17.14mC161.43mD1.714kmThe entropy change in melting 1g of ice at 0∘C. (Latent heat of ice is 80calg−1)
A23.07JK−1mol−1B20.07JK−1mol−1C22.07JK−1mol−1D21.07JK−1mol−1A coil of water of resistance 50Ω is embedded in a block of ice and a potential difference of 210 V is applied across it. The amount of ice which melts in 1 second is [ latent heat of fusion of ice =80calg−1]
A0.262gB2.62gC26.2gD0.0262g
One end of a copper rod of uniform cross-section and length 150 cm is in contact with ice and the other end with water at 100∘C . At what point along its length should a temperature of 200∘C be maintained so that in steady state, the mass of the ice melting is equal to that of steam produced in the same interval of time? Assume that whole system is insulated from the surroundings. Latent heat of steam =537calg−1 and lalent heat of fusion of ice =80calg−1.
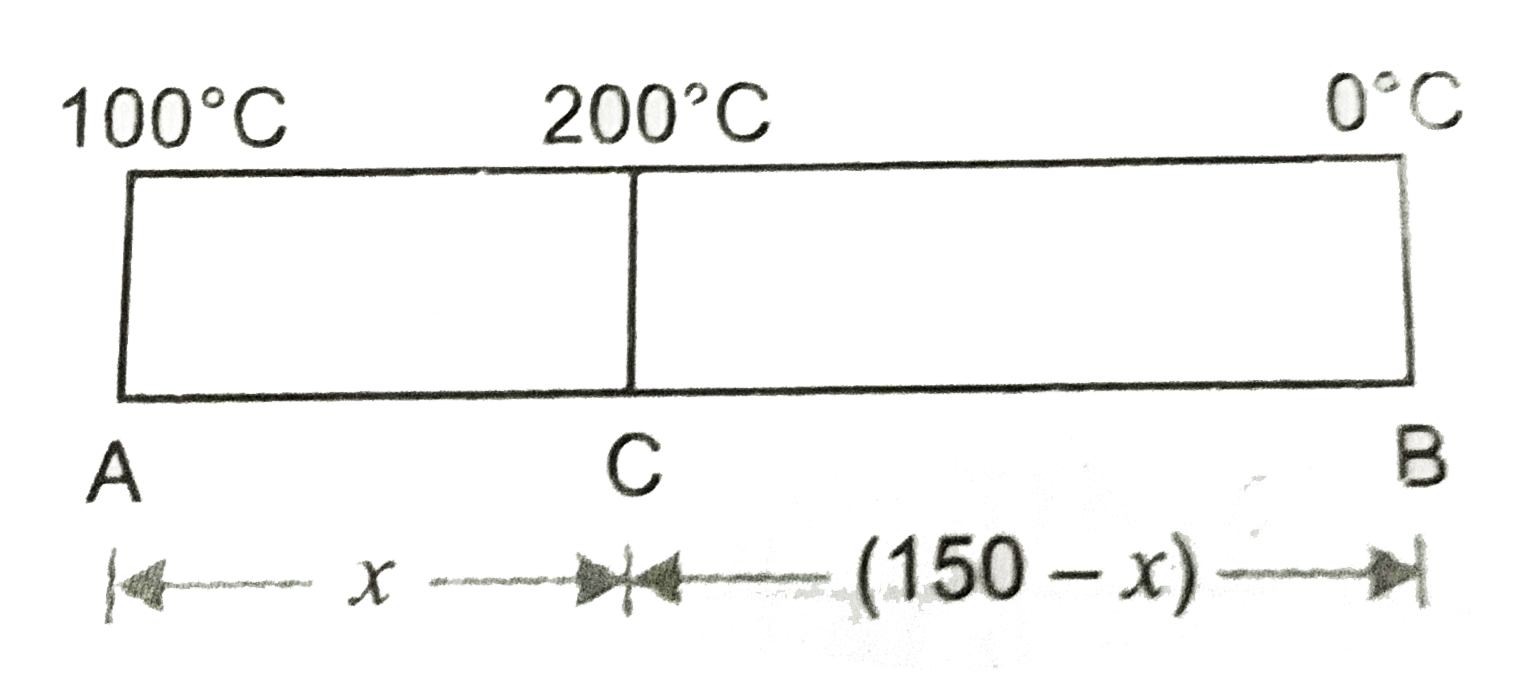 .
.
View SolutionCalculate the entropy change in the melting of 1 kg of ice at 0∘C in SI units. Heat of funsion of ice = 80 cal g−1.
View SolutionRays from the sun ar focuseed by a lens of diameter 5 cm on to a block of ice and 10 g of ice is melted in 20 min. Therefore the heat from the sun reaching the earth per min per square centrimetre is
(Latent heat of ice L=80calg−1)
View Solution2kg ice block should be dropped form 'x' km' height to melt completely. The 8 kg ice should be dropped from a height of
View SolutionA coil of wire of resistance 50Ω is embedded in a block of ice and a potential difference of 210 V is applied across it. The amount of ice which melts in 1 second is [ latent heat of fusion of ice =80calg−1]
View Solution

