A solid sphere of radius 10cm is subjected to a uniform pressure =5×108Nm2 . Determine the consequnt change in volume. Bulk modulus of the material of the sphere is equal to 3.14×1011Nm−2
To determine the consequent change in volume of a solid sphere subjected to a uniform pressure, we can use the relationship between bulk modulus, pressure, and change in volume. Here is a step-by-step solution:
Step 1: Understand the given parameters
- Radius of the sphere, r=10cm=0.1m
- Uniform pressure, P=5×108N/m2
- Bulk modulus of the material, K=3.14×1011N/m2
Step 2: Calculate the initial volume of the sphere
The volume V of a sphere is given by the formula:
V=43πr3
Substituting the radius:
V=43π(0.1)3=43π(0.001)=4π3000≈0.00418879m3
Step 3: Use the formula for change in volume
The change in volume ΔV due to the applied pressure can be calculated using the formula:
ΔV=P⋅VK
Where:
- P is the pressure,
- V is the initial volume,
- K is the bulk modulus.
Step 4: Substitute the values into the formula
Substituting the values we have:
ΔV=(5×108)⋅(0.00418879)3.14×1011
Step 5: Calculate the change in volume
Calculating the numerator:
5×108⋅0.00418879≈209.4395
Now, substituting this into the equation:
ΔV=209.43953.14×1011≈6.67×10−6m3
Final Result
The consequent change in volume of the sphere is approximately:
ΔV≈6.67×10−6m3
---
- Radius of the sphere, r=10cm=0.1m
- Uniform pressure, P=5×108N/m2
- Bulk modulus of the material, K=3.14×1011N/m2
The volume V of a sphere is given by the formula:
V=43πr3
Substituting the radius:
V=43π(0.1)3=43π(0.001)=4π3000≈0.00418879m3
The change in volume ΔV due to the applied pressure can be calculated using the formula:
ΔV=P⋅VK
Where:
- P is the pressure,
- V is the initial volume,
- K is the bulk modulus.
Substituting the values we have:
ΔV=(5×108)⋅(0.00418879)3.14×1011
Calculating the numerator:
5×108⋅0.00418879≈209.4395
Now, substituting this into the equation:
ΔV=209.43953.14×1011≈6.67×10−6m3
The consequent change in volume of the sphere is approximately:
ΔV≈6.67×10−6m3
Topper's Solved these Questions
Similar Questions
A wire increases by 10−3 of its length when a stress of 1×108Nm−2 is applied to it. What is the Young's modulus of the material of the wire?
View SolutionA block of vloume 1 m3 is subjected to a hydrostatic pressure of 1.3×105Nm−2. If the bulk modulus of the material of the block be 26×1012Nm2, what is the decrease in the volume of the block?
View Solution
Knowledge Check
A solid sphere of radius 0.2 m is subjected to a uniform pressure of 105N/m2. If the bulk modulus of the material is 1.6×1011N/m2, then the decrease in the volume of the sphere is approximately will be
A0.02m3B0.3cm3C0.4cm3D0.5cm3A sphere or radius 3 cm is subjected to a pressure of 100 atm. Its volume decreases by 0.3 cc. What will be its bulk modulus?
A4π×105atmB4π×3×103atmC4π×106atmD4π×108atmA liquid of volume 4 litere is subjected to additional pressure of 1.2×107N/m2. If the change in its volume is found to be 3 ml, then the bulk modulus of the liquid will be
A2.0×1010N/m2B1.6×1010N/m2C1.4×1010N/m2D2.4×1010N/m2
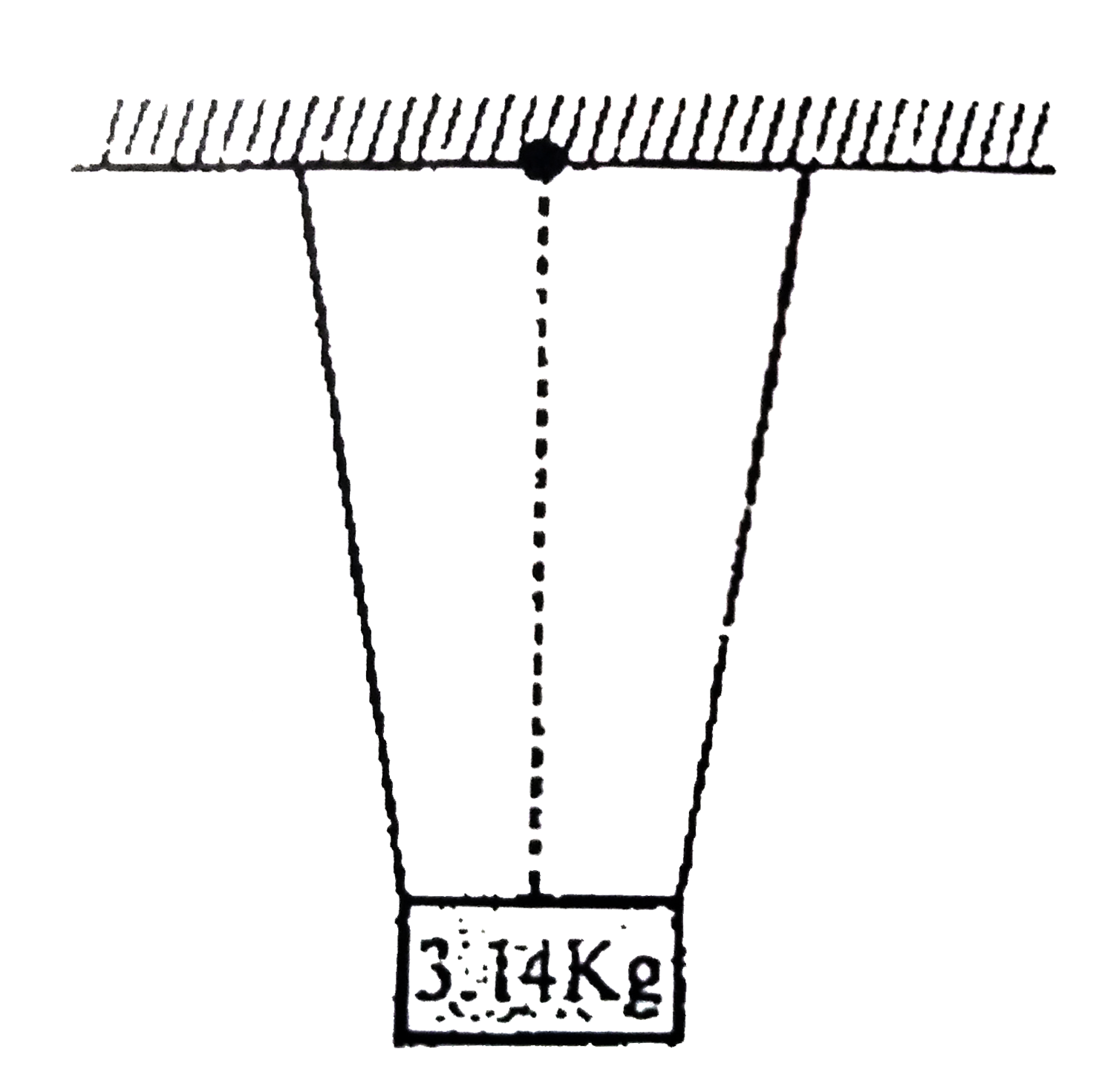
A body of mass 3.14 kg is suspended from one end of a non uniform wire of length 10m, such that the radius of the wire is changing uniformly from 9.8×10−4 m at one end to 5×10−4 m at the other end. Find the change in length of the wire in mm. Young's modulus of the material of the wire is 2×1011N/m2 (mass of wire is negligible)
View SolutionA solid copper cube 10 cm on an edge is subjected to a pressure of 7 MPa. The volume change of the metal cube will be, (bulk modulus of copper = 140 GPa)
View SolutionA spherical ball contracts in volume by 0.02% when subjected to a normal uniform pressure of 200 atmospheres. Then Bulk modulus (in N/m2) of the material of the ball is
(Atomospheric pressure =105N/m2)
View SolutionA uniform cylindrical wire is subjected to a longitudinal tensile stress of 5×107N/m2. Young's modulus of the material of the wire is 2×1011N/m2. The volume change in the wire is 0.02%. The factional change in the radius is
View SolutionA conducting sphere of radius 10 cm is given a charge of +2×10−8C. What will be its potential?
View Solution

