A piece of wood of mass 0.03 kg is dropped from the top of a building 100 m high. At the same time, a bullet of mass 0.02 kg is fired vertically upward with a velocity of 100 m/s from the ground the bullet gets embedded in the wooded piece after striking. find the height to which the combination rises above the building before it starts falling take g=10m/s2
Step by step video & image solution for A piece of wood of mass 0.03 kg is dropped from the top of a building 100 m high. At the same time, a bullet of mass 0.02 kg is fired vertically upward with a velocity of 100 m/s from the ground the bullet gets embedded in the wooded piece after striking. find the height to which the combination rises above the building before it starts falling take g=10m//s^(2) by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- LAWS OF MOTION : FRICTIONBook:SL ARORAChapter:LAWS OF MOTION : FRICTIONExercise:Self Practice
Explore 95 Videos
- LAWS OF MOTION : FRICTIONBook:SL ARORAChapter:LAWS OF MOTION : FRICTIONExercise:Self Practice
Explore 95 Videos
- Laws of MotionBook:SL ARORAChapter:Laws of MotionExercise:Exercise
Explore 627 Videos
- Mathematical toolsBook:SL ARORAChapter:Mathematical toolsExercise:Exercise
Explore 20 Videos
Similar Questions
A wooden block of mass 10g is dropped from the top of a cliff 100 m high. Simultaneously, a bullet of mass 10 g is fired from the foot of the cliff vertically upwards with a velocity of . 100m/s
(i) Where and after what time will they meet
(ii) If the bullet after striking the block gets embedded in it how high will it rise above the cliff before it starts falling
View SolutionA wooden block is dropped from the top of a cliff 100m high and simultaneously a bullet of mass 10 g is fired from the foot of the cliff upwards with a velocity of 100m/s. The bullet and wooden block will meet each other after a time:
View Solution
Knowledge Check
A piece of wood of mass 0.3 kg is dropped from the top of a 20 m height building. At the same time, a bullet of mass 0.2 kg is fired vertically upward, with a velocity 80m/s from the ground. The bullet strikes the wood and gets embedded in it. Then, the maximum height to which the combined system reaches above the top of the building before falling below is: (g=10m/s2)
A20mB5mC43.2 mD35mA wooden block of mass 10g is dropped from the top of a tower 100m high. Simultaneously, a bullet of mass 10g is fired from the foot of the tower vertically upwards with a velocity of 100m/s. If the bullet is embedded in it, how high will the block rise above the top of tower before it starts falling? (g=10m/s2)
 A75mB85mC80mD10m
A75mB85mC80mD10mA wooden block of mass 10gm is dropped from the top of a tower 100m high. Simultaneously, a bullet of mass 10gm is fired from the foot of the tower vertically upwards with a velocity of 100m/sec, figure. If the bullet is embedded in it, how high will it rise above the tower before it starts falling ? (Consider g=10m/sec2)
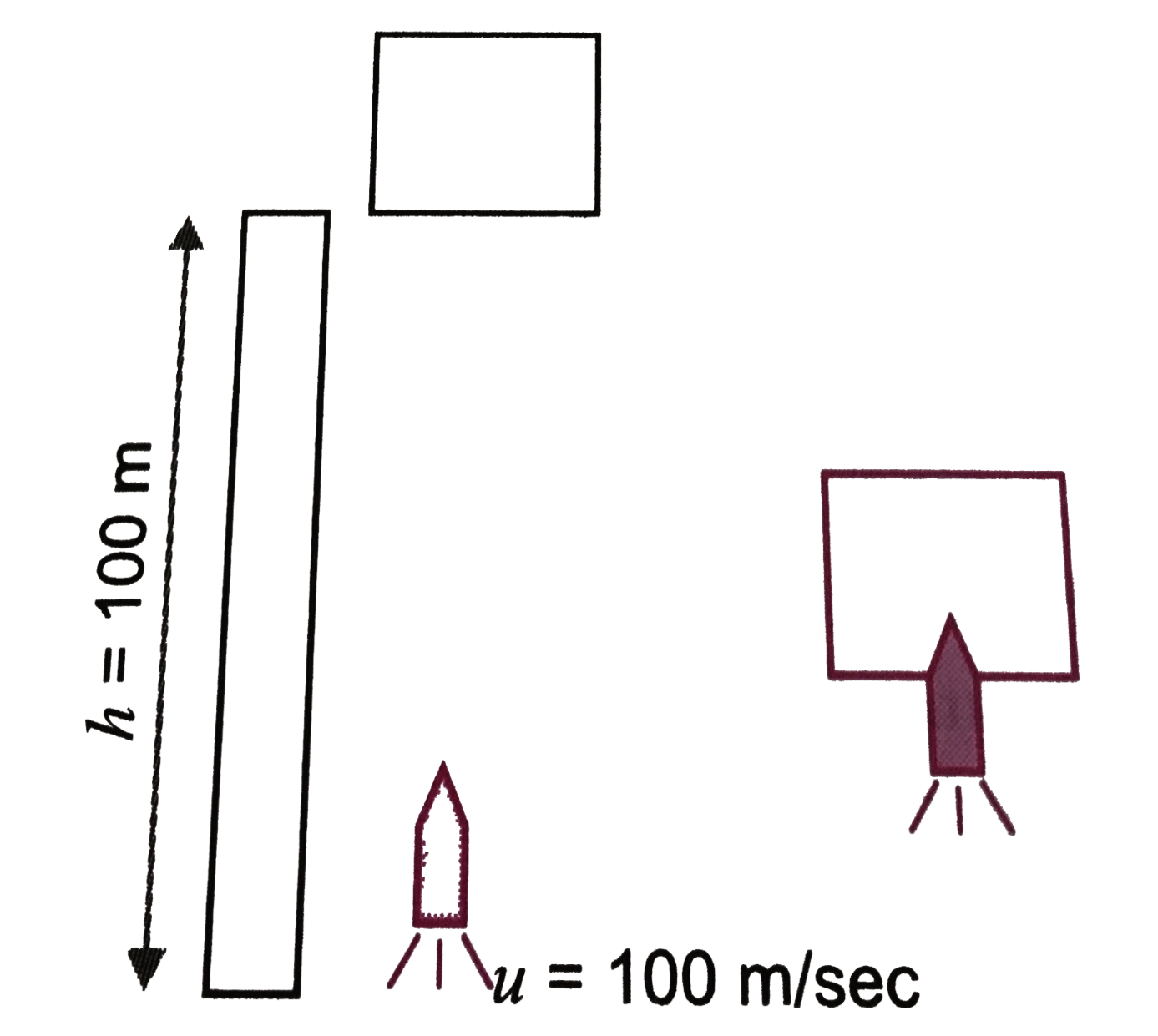 A80mB85mC75mD10m
A80mB85mC75mD10m
A bullet of mass 10 g is fired with a velocity of 20 m/s from a gun of mass 2 kg. Find the recoil velocity (in m/s) of the gun.
View SolutionA bullet of mass 10 g is fired with a velocity of 100 m/s from a rifle of mass 2.5 kg, the recoil velocity of the rifle is
View SolutionA wooden block of mass 20g is dropped from the top of the cliff 50 m high. Simultaneously a bullet of mass 20 g is fired from the foot of the cliff upwards with a velocity 25 ms−1. The bullet and the wooden block will meet each other after time :
View SolutionA bullet of mass 10gm is fired with a velocity of 40 m/s from a gun of mass 8 kg. Find the recoil velocity (in m/s) of the gun.
View SolutionA wooden block of mass 10gm is dropped from the top of a cliff 100m high. Simultaneously a bullet of same mass is fired from the foot of the cliff vertically upwards with a velocity of 100ms−1. If the bullet after collision gets embedded in the block, the common velocity of the bullet and the block immediately after collision is (g=10ms−2).
View Solution

