A solid uniform sphere rotating about its axis with kinetic energy E1 is gently placed on a rough horizontal plane at time t=0, Assume that, at time t=t1, it starts pure rolling and at that instant total KE of the sphere is E2. After sometime, at time t=t2. KE of the sphere is E3. Then
E1=E2=E3
E1>E2=E3
E1>E2>E3
E1<E2=E3
The correct Answer is:B
Step by step video, text & image solution for A solid uniform sphere rotating about its axis with kinetic energy E_(1) is gently placed on a rough horizontal plane at time t=0, Assume that, at time t=t_(1), it starts pure rolling and at that instant total KE of the sphere is E_(2). After sometime, at time t=t_(2). KE of the sphere is E_(3). Then by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - DC PANDEYCHAPTER - ROTATIONAL MOTIONEXERCISE - A Only One Option is Correct
86 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEYCHAPTER - ROTATIONAL MOTIONEXERCISE - More than one option is correct
36 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEYCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
Similar Questions
A solid sphere of radius 2.45m is rotating with an angular speed of 10rad/s. When this rotating sphere is placed on a rough horizontal surface then after sometime it starts pure rolling. Find the linear speed of the sphere after it starts pure rolling.
View SolutionA uniform disc of mass m and radius R is projected horizontally with velocity v0 on a rough horizontal floor so that it starts with a purely sliding motion at t= 0. After t0 seconds it acquires a purely rolling motion.
(a) Calculate the velocity of the centre of mass of the disc at t0
(b) Assuming the coefficient of friction to be μ, calculate to. Also calculate the work done by the frictional force as a function of time and the total work done by it over a time t muchlonger than t0.
View Solution
Knowledge Check
A sphere is rolling on a horizontal surface without slipping. The ratio of the rotational K.E. to the total kinetic energy of the sphere is
A25B27C57D37A long horizontal plank of mass m is lying on a smooth horizontal surface. A sphere of same mass m and radius r is spinned about its own axis with angular velocity we and gently placed on the plank. The coefficient of friction between the plank and the sphere is μ. After some time the pure rolling of the sphere on the plank will start. Answer the following questions.

Find the displacement of the plank till the sphere starts pure rolling.Aω20r281μgB227ω20r2μgC481ω20r2μgD281ω20r281μgA long horizontal plank of mass m is lying on a smooth horizontal surface. A sphere of same mass m and radius r is spinned about its own axis with angular velocity we and gently placed on the plank. The coefficient of friction between the plank and the sphere is μ. After some time the pure rolling of the sphere on the plank will start. Answer the following questions.
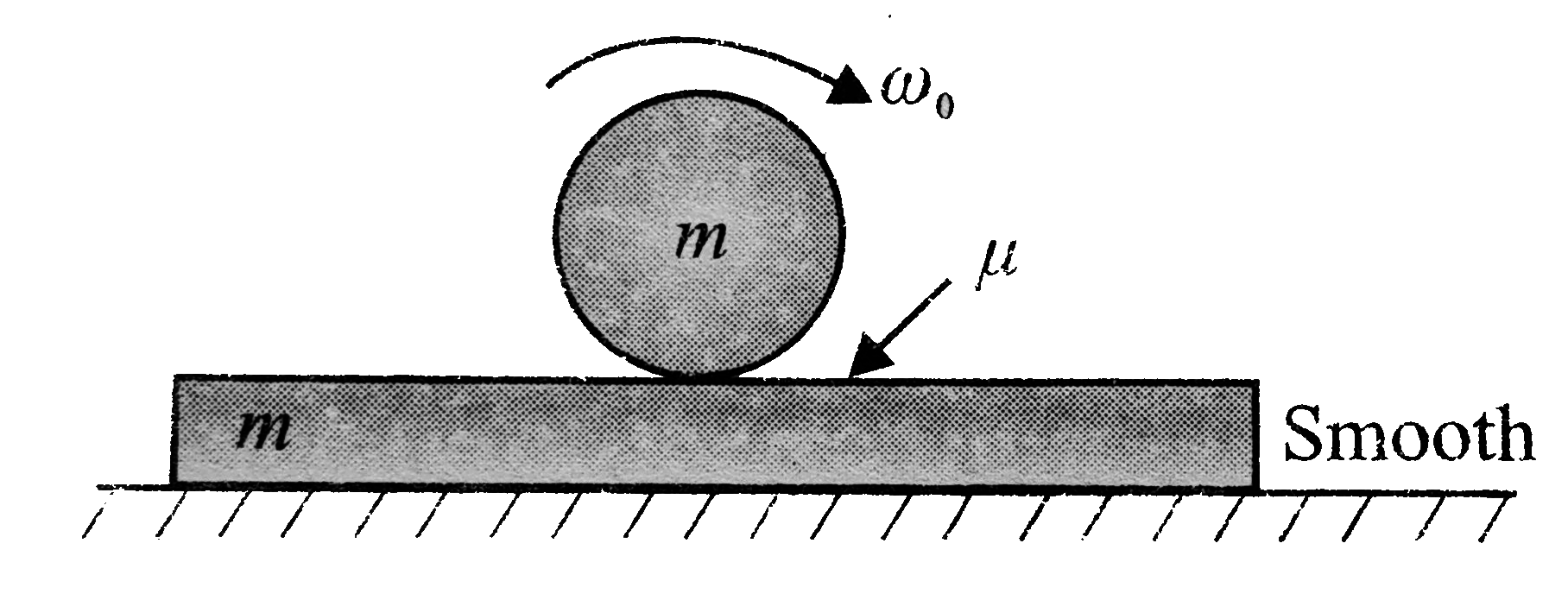
Find the time t at which the pure roiling startsAω0r9μgB2ω0r9μgCω0r3μgD2ω0rμg
A sphere of mass m rolls on a plane surface.Find its kinetic energy t an instant when its centre moves with speed v.
View SolutionA solid sphere is rolling on a frictionless plane surface about the axis of symmetry. Find the rotational energy of the sphere. Also, find the ratio of rotational K.E. to total energy.
View SolutionA long horizontal plank of mass m is lying on a smooth horizontal surface. A sphere of same mass m and radius r is spinned about its own axis with angular velocity we and gently placed on the plank. The coefficient of friction between the plank and the sphere is μ. After some time the pure rolling of the sphere on the plank will start. Answer the following questions.
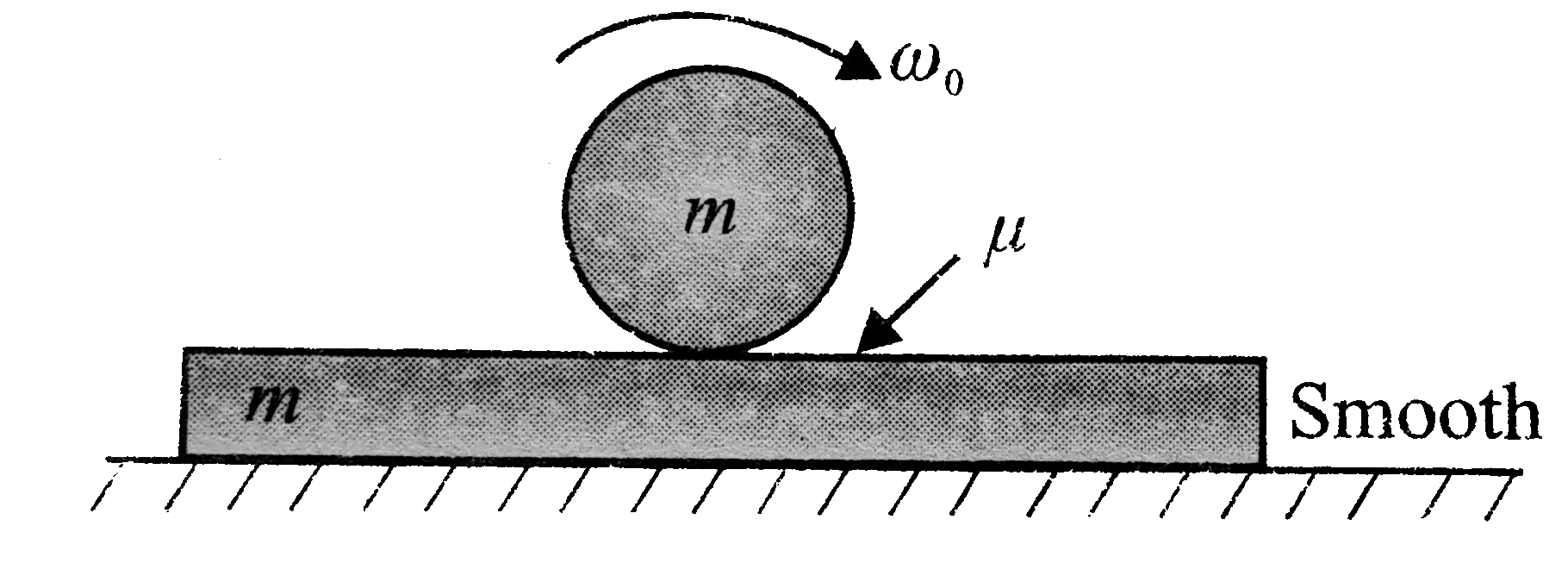
Find the velocity of the sphere after the pure rolling starts
View SolutionA solid sphere and a hollow sphere of equal mass and radius are placed over a rough horizontal surface after rotating it about its mass centre with same angular velocity ω0. Once the pure rolling starts let v1 and v2 be the linear speeds of their centres of mass. Then
View SolutionA long horizontal plank of mass m is lying on a smooth horizontal surface. A sphere of same mass m and radius r is spinned about its own axis with angular velocity we and gently placed on the plank. The coefficient of friction between the plank and the sphere is μ. After some time the pure rolling of the sphere on the plank will start. Answer the following questions.

Find the velocity of the sphere after the pure rolling starts
View Solution
