A block of mass M slides along a horizontal table with speed v0. At x=0, it hits a spring with spring constant k and begins to experience a friction force. The coefficient of friction is variable and is given by μ=bx, where b is a positive constant. Find the loss in mechanical energy when the block has first come momentarily to rest.
 .
.
gbMv202k
Mgbv202(k+gb)
gbMv20k
M2gbv202(k+Mgb)
The correct Answer is:D
Step by step video, text & image solution for A block of mass M slides along a horizontal table with speed v_(0). At x=0, it hits a spring with spring constant k and begins to experience a friction force. The coefficient of friction is variable and is given by mu=bx, where b is a positive constant. Find the loss in mechanical energy when the block has first come momentarily to rest. . by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- WORK, POWER AND ENERGYBook:DC PANDEYChapter:WORK, POWER AND ENERGYExercise:B More than One Option is Correct
Explore 26 Videos
- WORK, POWER AND ENERGYBook:DC PANDEYChapter:WORK, POWER AND ENERGYExercise:C Comprehension Type Questions
Explore 18 Videos
- WORK, POWER AND ENERGYBook:DC PANDEYChapter:WORK, POWER AND ENERGYExercise:E Integer Type Questions
Explore 11 Videos
- WORK, ENERGY AND POWERBook:DC PANDEYChapter:WORK, ENERGY AND POWERExercise:MEDICAL ENTRACES GALLERY
Explore 33 Videos
Similar Questions
A block of mass m is kept on a horizontal table. If the static friction coefficient is μ., find the frictional force acting on the block.
View SolutionA block of mass m moving with a velocity v0 on a rough horizontal surface from x=0 coefficient of friction is given by μ=μ0=ax. Find the kinetic energy of the block as function of x before it comes to rest.
View Solution
Knowledge Check
A block of mass m is moving with a speed v on a horizontal rough surface and collides with a horizontal mounted spring of spring constant k as shown in the figure .The coefficient of friction between the block and the floor is μ The maximum compression of the spring is
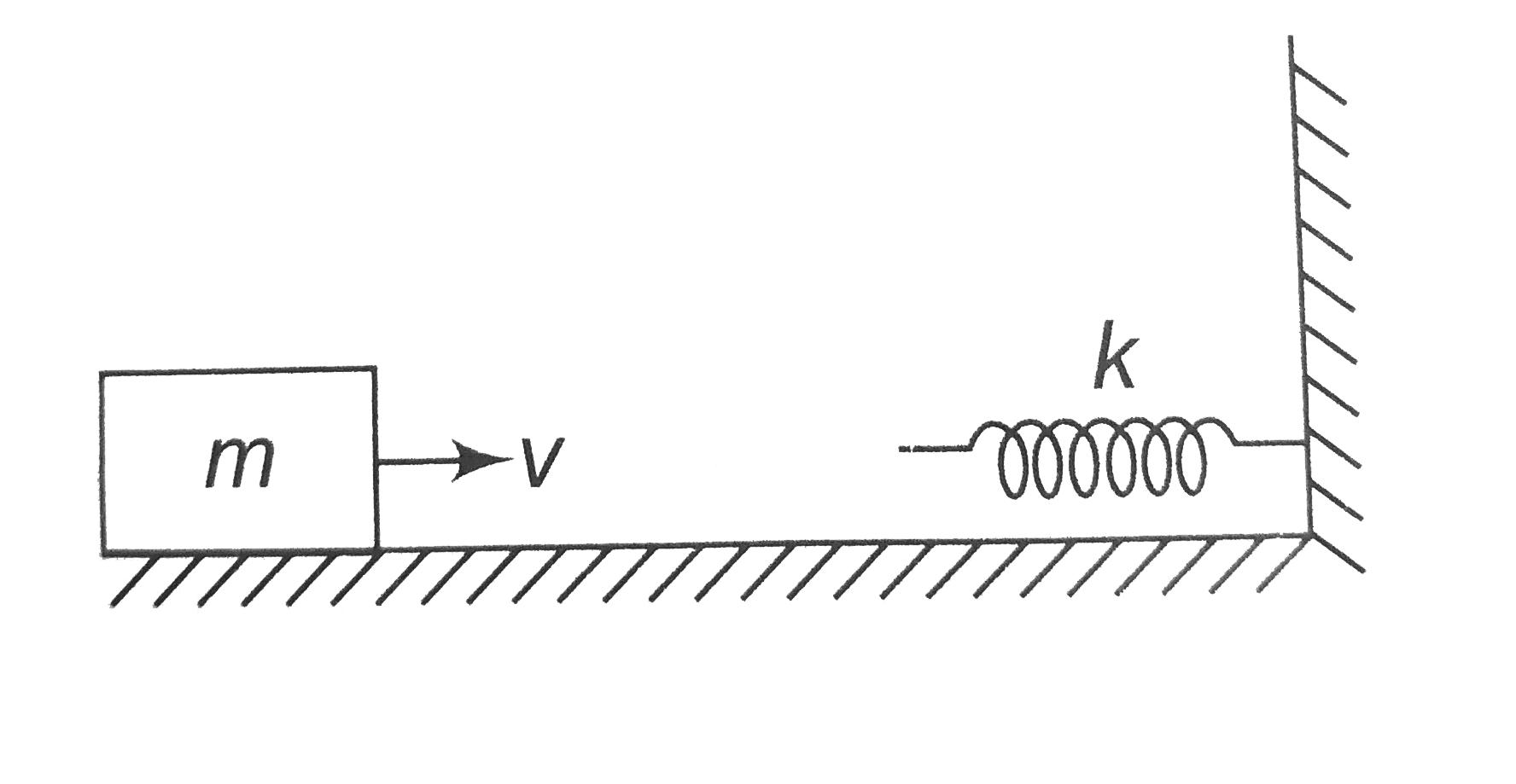 A−μmgk+1k√(μmg)2+mkv2Bμmgk+1k√(μmg)2+mkv2C−μmgk+1k√(μmg)2−mkv2Dμmgk+1k√(μmg)2+mkv2
A−μmgk+1k√(μmg)2+mkv2Bμmgk+1k√(μmg)2+mkv2C−μmgk+1k√(μmg)2−mkv2Dμmgk+1k√(μmg)2+mkv2A block of mass m moving with velocity v0 on a smooth horizontal surface hits the spring of constant k as shown. Two maximum compression in spring is
 A√2mkv0B√mk.v0C√mk.v0Dm2k.v0
A√2mkv0B√mk.v0C√mk.v0Dm2k.v0A block of mass 4kg slides on a horizontal frictionless surface with a speed of 2m/s. It is brought to rest in compressing a spring in its path. If the force constant of the spring is 400N/m, by how much the spring will be compressed
A2×10−2mB0.2mC20mD200m
A block of mass m slides 0n a frictionless table. It is constrained to move inside a ring of radius R . At time t=0 , block is moving along the inside of the ring (i.e. in the tangential direction) with velocity v0 . The coefficient of friction between the block and the ring is μ . Find the speed of the block at time t .

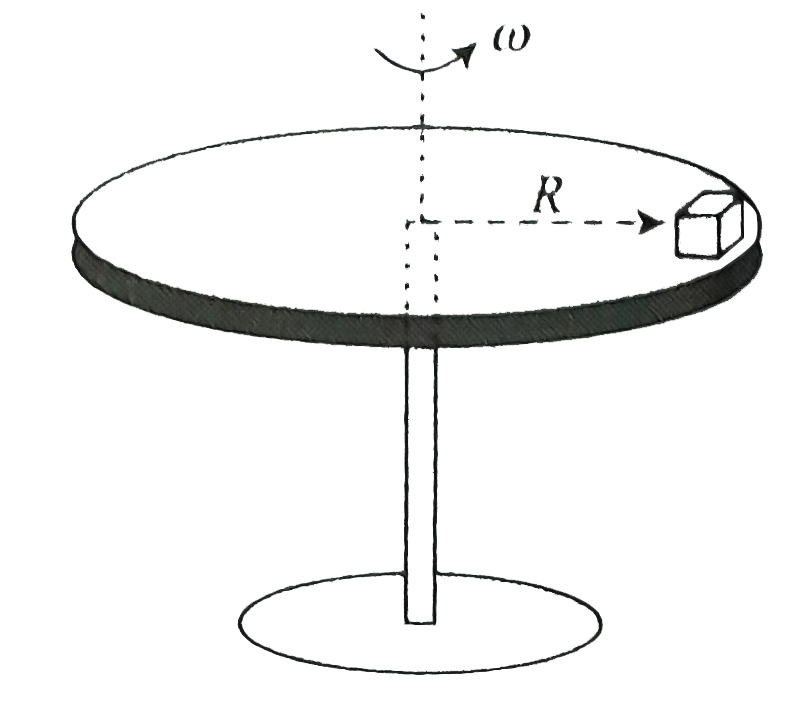
View SolutionA block of mass m is kept on the edge of a horizontal turn table of radius R which is rotating with constant angular verticle ω (along with the block ) about its axis . If coefficient of friction is μ, find the friction force between block and table.
View SolutionA block of mass m, lying on a smooth horizontal surface, is attached to a spring (of negligible mass) of spring constant k. The other end of the spring is fixed, as shown in the figure. The block is initally at rest in its equilibrium position. If now the block is pulled withe a constant force F, the maximum speed of the block is :

View SolutionA block of mass m, lying on a smooth horizontal surface, is attached to a spring (of negligible mass) of spring constant k. The other end of the spring is fixed, as shown in the figure. The block is initally at rest in its equilibrium position. If now the block is pulled withe a constant force F, the maximum speed of the block is :

View SolutionIn the position shown in figure, the spring is at its natural length. The block of mass m is given a velocity v0 towards the vertical support at t=0. The coefficient of friction between the block and the surface is given by μ=αx, where α is a positive constant and x is the position of the block from its starting position. The block comes to rest for the first time at x, which is
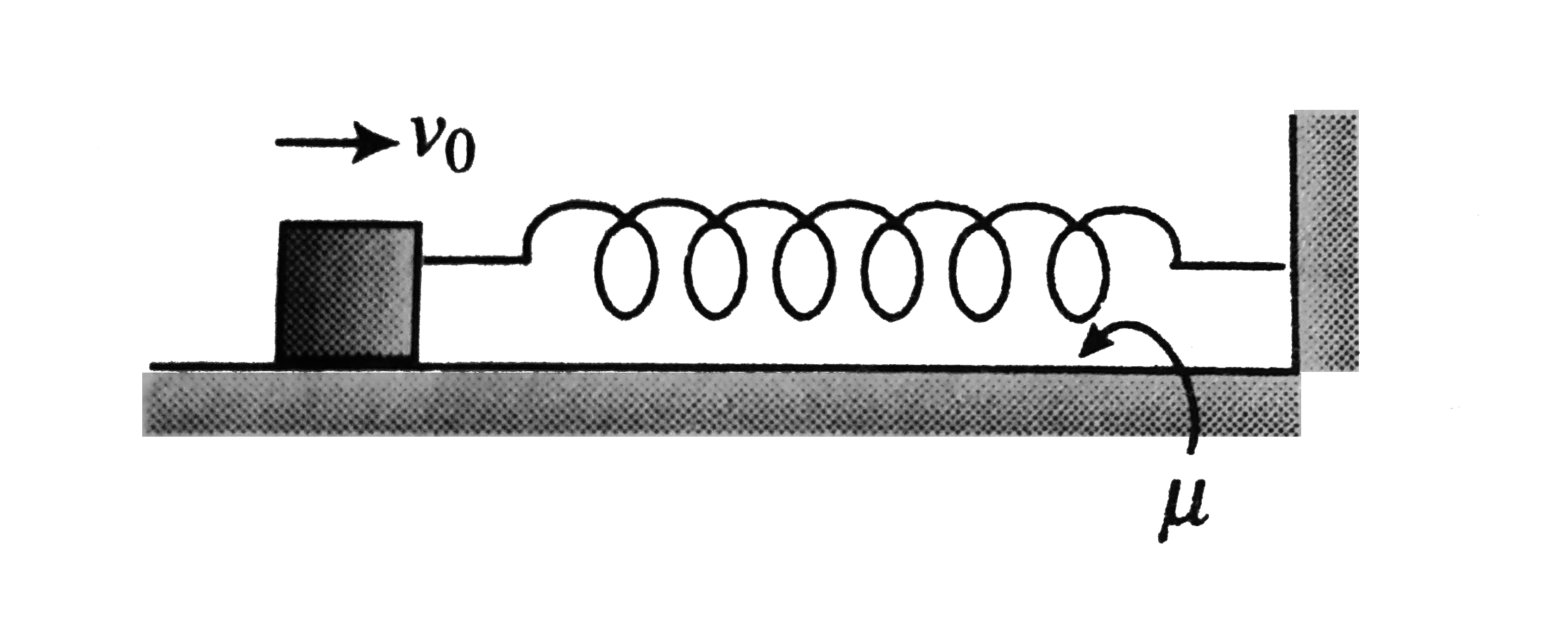
View Solution

