A block of mass 250 g is kept on a vertical spring of spring constant 100 N/m fixed from below. The spring is now compressed to have length 10 cm shorter than its natural length and the system is released from this position. How high does the block rise? take g=10ms2.
20 cm
30 cm
40 cm
50 cm
The correct Answer is:A
Step by step video, text & image solution for A block of mass 250 g is kept on a vertical spring of spring constant 100 N/m fixed from below. The spring is now compressed to have length 10 cm shorter than its natural length and the system is released from this position. How high does the block rise? take g=10 m/s^2. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - WORK, POWER AND ENERGYEXERCISE - A Only One Option is Correct42videos
WORK, POWER AND ENERGY
- BOOK - DC PANDEYCHAPTER - WORK, POWER AND ENERGYEXERCISE - B More than One Option is Correct26videos
WORK, POWER AND ENERGY
- BOOK - DC PANDEYCHAPTER - WORK, ENERGY AND POWEREXERCISE - MEDICAL ENTRACES GALLERY33videos
WORK, ENERGY AND POWER
Similar Questions
A block o fmass 250 is g is kept on a vertical spring of spring constant 100 N/m fixed from below. The spring is now compressed to have length 10 cm shorter than its natural length and the system is released from this position. How high does the block rise? take g=10ms2.
View SolutionThe pulley shown in figure has a radius of 20 cm and moment of inertial 0.2 kg-m^2. The string going over it is attached at one end to a vertical sprign of spring constant 50 N/m fixed from below and supports a 1 kg mas at other end. The system is released from rest with the spring at its natural length. Find the speed of the block when it has desceds through 10 cm. Take g=10ms2.
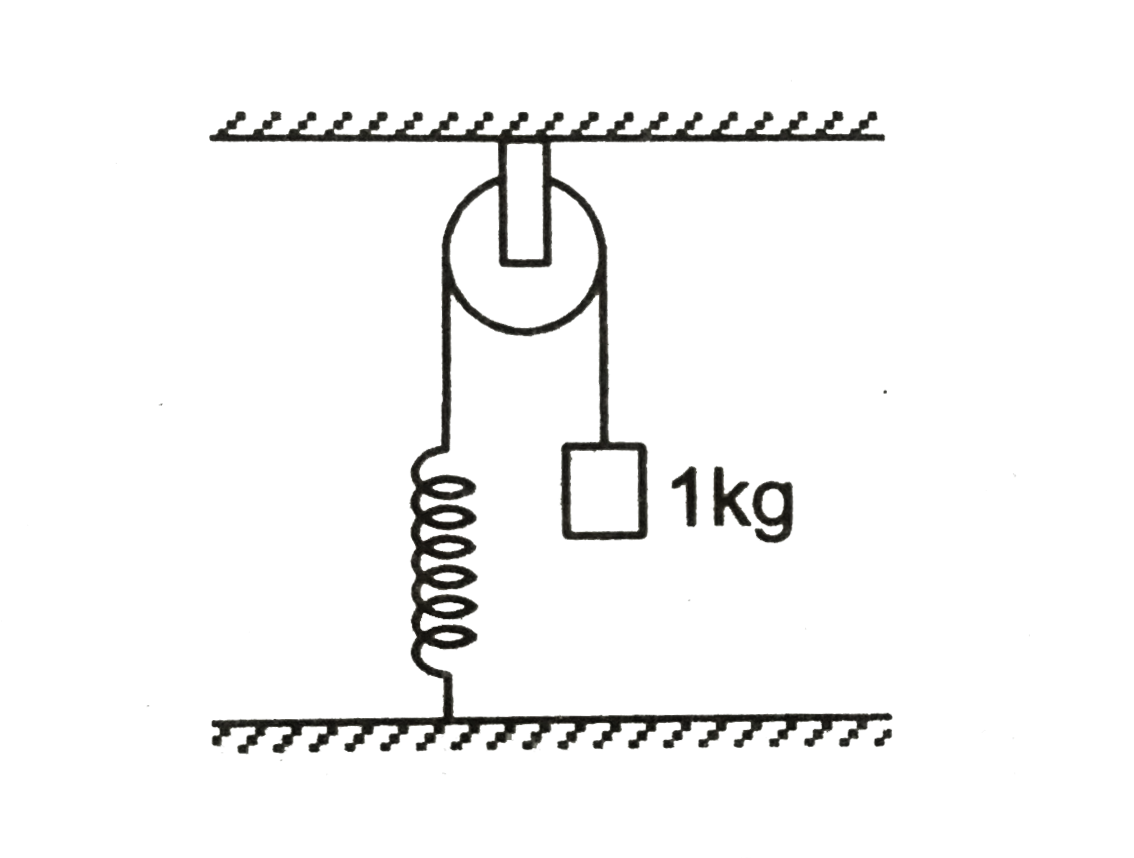
View Solution
Knowledge Check
- Question 1 - Select One
A toy gun uses a spring of spring constant 1000 N/m . If spring is compressed by an amount 10 cm before fire then how high can be bullet be fired if mass of each bullet is 10 g .
A30 mB40 mC50 mD60 m - Question 2 - Select One
Find the maximum tension in the spring if initially spring at its natural length when block is released from rest.
AmgBmg/2C3mg/2D2 mg
A planck of mass 5kg is placed on a frictionless horizontal plane. Further a block of mass 1kg is placed over the plank. A massless spring of natural length 2m is fixed to the plank by its one end. The other end of spring is compressed by the block by half of spring's natural length. They system is now released from the rest. What is the velocity of the plank when block leaves the plank? (The stiffness constant of spring is 100N/m)
View SolutionA block of mass m hangs from a vertical spring of spring constant k. If it is displaced from its equilibrium position, find the time period of oscillations.
View SolutionA block of mass 1kg is connected with massless spring of constant 100N/m .At t=0 ,a constant force F=10N is applied on the block. The spring is in its natural length at t=0.The speed of particle at x=6cm form mean position is
View SolutionA block of mass 180g is placed on a spring (spring constant k=120N/m) fixed from below. A ball of mass 20g is dropped from height 20m and the collision is completely inelastic. Find the maximum compression of the spring. Neglect the initial compression of the spring due to the block.
View Solution
A block of mass m is pushed against a spring of spring constant k fixed at one end to a wall.The block can slide on a frictionless table as shown in the figure. The natural length of the spring is L0 and it is compressed to one fourth of natural length and the block is released.Find its velocity as a function of its distance (x) from the wall and maximum velocity of the block. 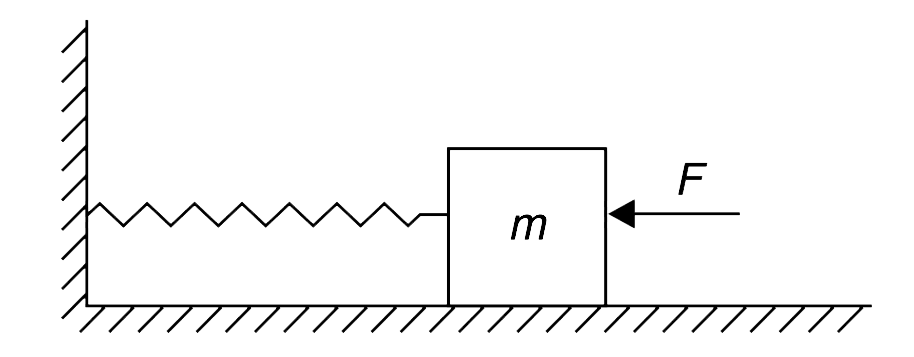The block is not attached to the spring.View SolutionA block of mass m = 1 kg is kept pressed against a spring on a rough horizontal surface. The spring is compressed by 10 cm from its natural length and to keep the block at rest in this position a horizontal force (F) towards left is applied. It was found that the block can be kept at rest if 8N≤F≤18N. Find the spring constant (k) and the coefficient of friction (μ) between the block and the horizontal surface.
View Solution