Potential energy v/s position curve for one dimensional conservative field is shown. Force at A and B is respectively.

Positive, Positive
Positive, Negative
Negative, Positive
Negative, Negative
The correct Answer is:B
Step by step video, text & image solution for Potential energy v//s position curve for one dimensional conservative field is shown. Force at A and B is respectively. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- WORK, POWER AND ENERGYBook:DC PANDEYChapter:WORK, POWER AND ENERGYExercise:A Only One Option is Correct
Explore 42 Videos
- WORK, POWER AND ENERGYBook:DC PANDEYChapter:WORK, POWER AND ENERGYExercise:B More than One Option is Correct
Explore 26 Videos
- WORK, ENERGY AND POWERBook:DC PANDEYChapter:WORK, ENERGY AND POWERExercise:MEDICAL ENTRACES GALLERY
Explore 33 Videos
Similar Questions
Potential energy of a body in position A is-40J. Work done by conservative force in moving the body from A to B is−20J. Find potential energy of the body in position B.
View SolutionPotential energy (U) of a body of unit mass moving in a one-dimension conservative force field is given by, U=(X2−4X+3). All units are in S.I.
View Solution
Knowledge Check
The potential energy U of a body of unit mass moving in one dimensional conservative force field is given by U=x2−4x+3. All units are is SI. For this situation mark out the correct statement (s).
AThe body will perform simple harmonic motion about x=2 units.BThe body will perform oscillatory motion but not simple harmonic motion.CThe body will perform simple harmonic motion with time period √2πs.DIf speed of the body at equilibrium position is 4ms, then the amplitude of oscillation would be 2√2mThe potential energy of a particle in a conservative field is U=ar3−br2 , where a and b are positive constants and r is the distance of particle from the centre of field. For equilibrium, the value of r is
A2abB3a2bCa2bDabFigure given below shows the variation of potential energy function U(x), corresponding to a particle lying in a one dimensional force field. The force acting on the particle at x = 2 m is:
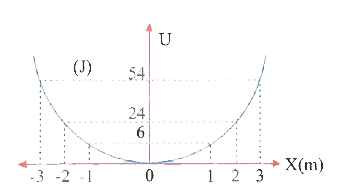 A−12NB−24NC−16ND−8N
A−12NB−24NC−16ND−8N
The potential energy of a particle in a conservative field is U=ar3−br2 where a and b are positive constants and r is the distance of particle from the centre of field. For equilibrium, the value of r is
View SolutionThe potential energy ‘V’ of a particle moving along the positive x-direction in a conservative force field varies as shown in the figure. The total energy is E=2. Draw the corresponding kinetic energy K vs x graph.
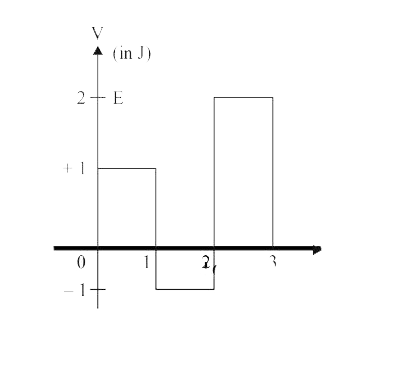
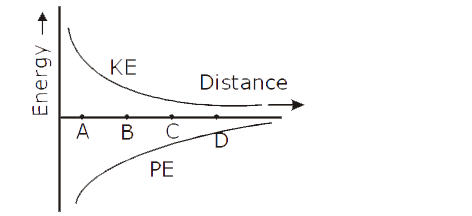
View SolutionPotential energy and kinetic energy of a two particle system under imaginary force field are shown by curves KE and PE. respectively in figure. This system is bound at :
View SolutionA : The potential energy can be defined only in conservative field.
R : The value of potential energy depends on the reference level (level of zero potential energy).
View SolutionGravitational force is a conservation and medium independent force. Its nature is attractive. Gravitational field intensity and gravitational potential gives information about gravitational fied in vector and scaler form respectively. Actually gravitational fied intensity is equal to the negative of the negative of teh potential gradient. potential energy is defined for only conservation force. it is also equal to the total energy in escaping condition. gravitational potential is either negative or zero but can never be positive due to attractive nature of gravitational force.
A person brings a mass of 1kg from infinity to a point A. Initially the mass was at rest but it moves with a speed of 2m/s as it reaches A. The work done by the person on a mass is −3J. The potential of A is:
View Solution

