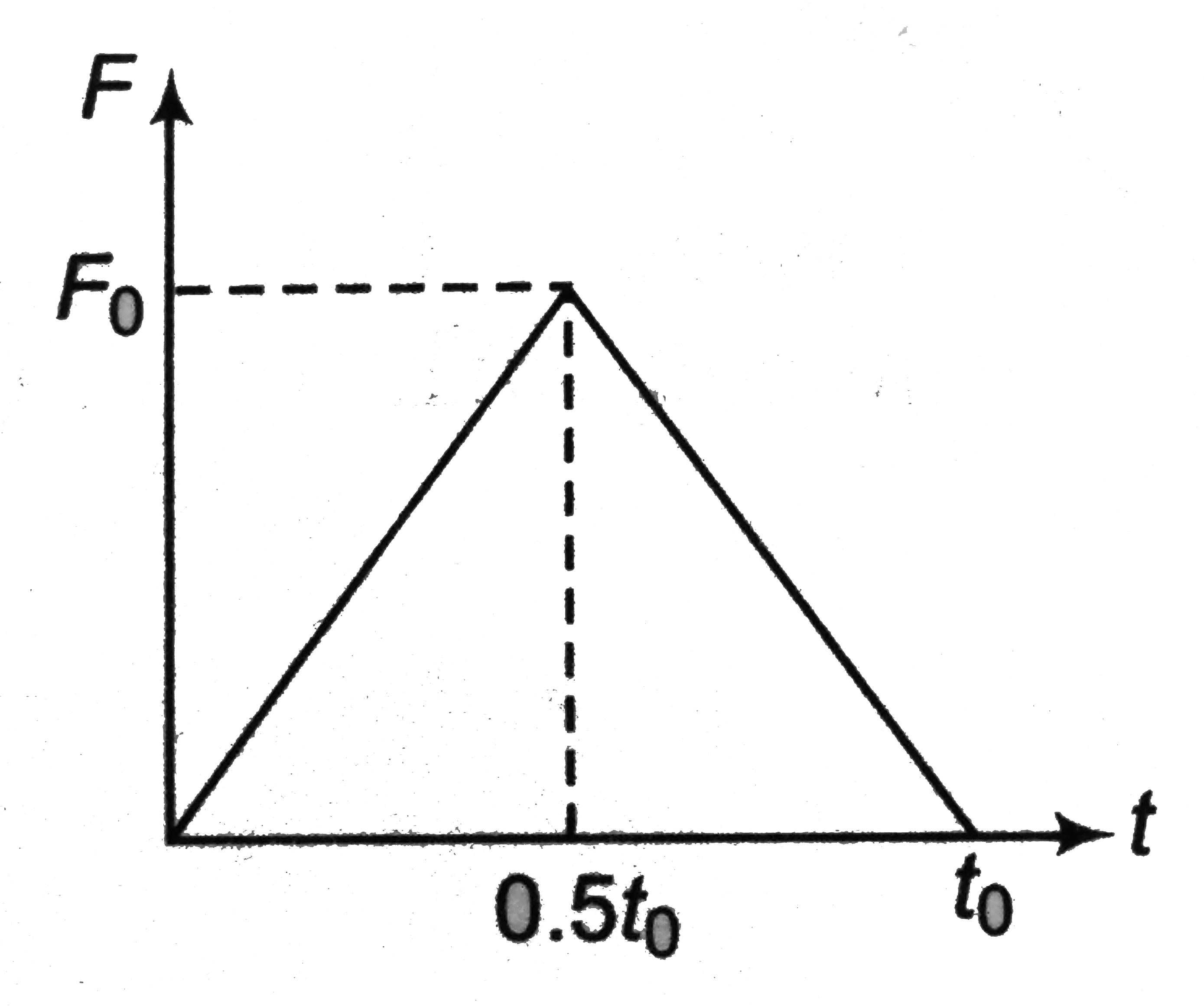
A particle of mass m moving with velocity u makes an elastic one-dimentional collision with a stationary particle of mass m. They come in contact for a very small time t0. Their force of interaction increases from zero to F0 linearly in time 0.5t0, and decreases linearly to zero in further time 0.5t0 as shown in figure. The magnitude of F0 is
μT
2μT
μ2T
None of these
The correct Answer is:B
In one dimensional elastic collision, between two equal masses velocities are interchanged. Therefore, change in linear momentum of any of the particle will be mu. Now impulse or area under F-T graph gives the change in linear momenntum.
∴12F0T=μ
or F0=2μT
Topper's Solved these Questions
- CENTRE OF MASSBook:DC PANDEYChapter:CENTRE OF MASSExercise:Assertion and reason
Explore 21 Videos
- CENTRE OF MASSBook:DC PANDEYChapter:CENTRE OF MASSExercise:Match the coloumns
Explore 9 Videos
- CENTRE OF MASSBook:DC PANDEYChapter:CENTRE OF MASSExercise:Check points
Explore 50 Videos
- CALORIMETRY AND HEAT TRANSFERBook:DC PANDEYChapter:CALORIMETRY AND HEAT TRANSFERExercise:Medical entrance s gallery
Explore 38 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBook:DC PANDEYChapter:CENTRE OF MASS, IMPULSE AND MOMENTUMExercise:Comprehension type questions
Explore 15 Videos
Similar Questions
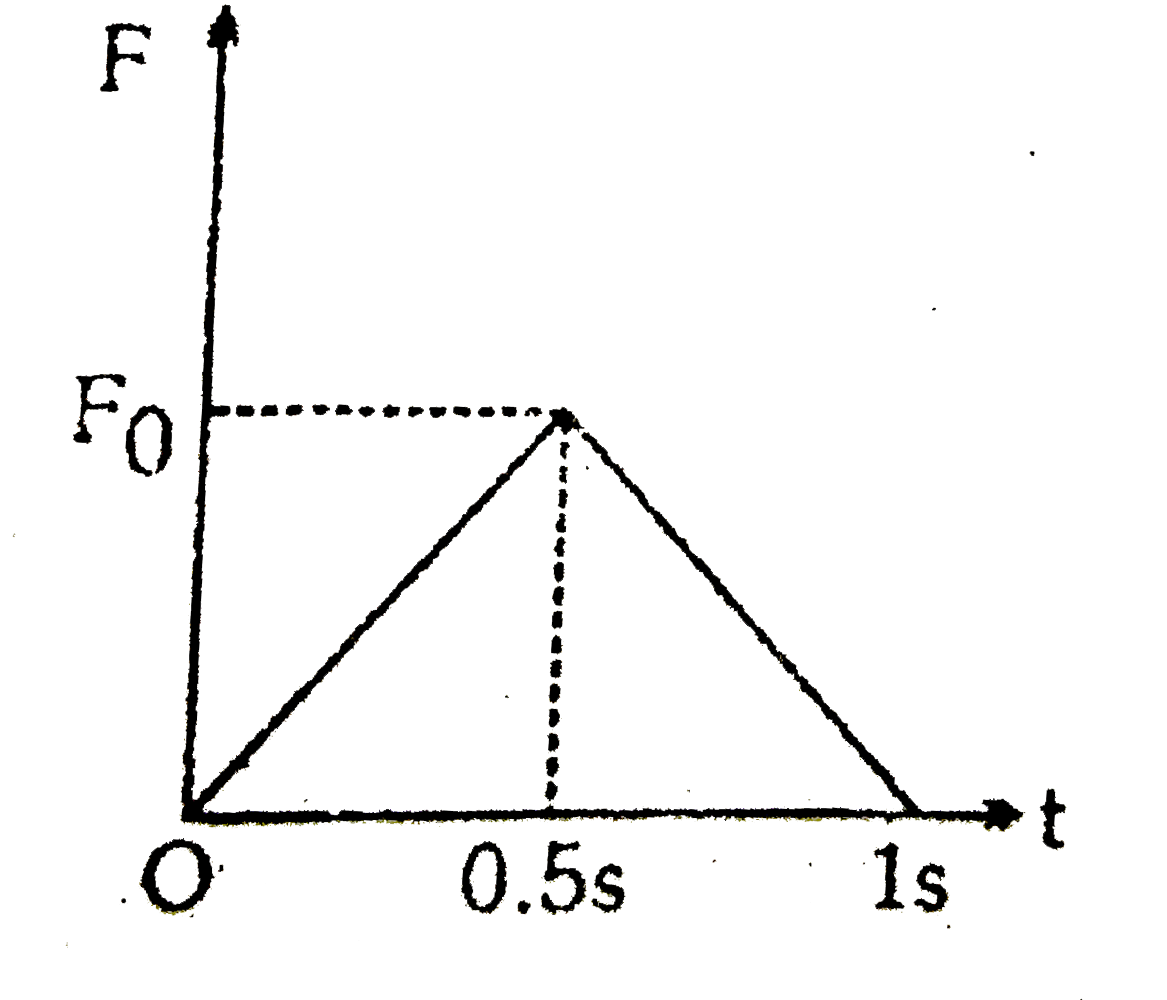
A body of mass 1kg moving with velocity 1ms makes an elastic one dimensional collision with an identical stationary body. They are in contact for brief time 1(~s). Their force of interaction increases from zero to F0 linearly in time 0.5s and decreases linearly to zero in further time 0.5s as shown in the figure. The magnitude of force F0 (in newton) is
'(##CEN_KSR_PHY_JEE_C08_E01_009_Q05##)'
View SolutionA body of mass 1kg moving with velocity 1m/s makes an elastic one dimesional collision with an identical stationary body. They are in contact for brief time 1sec. Their force of interaction increases form zero to F0 linearly in time 0.5s and decreases linearly to zero in further time 0.5sec as shown in figure. Find the magnitude of force F0 in newton.
View Solution
Knowledge Check
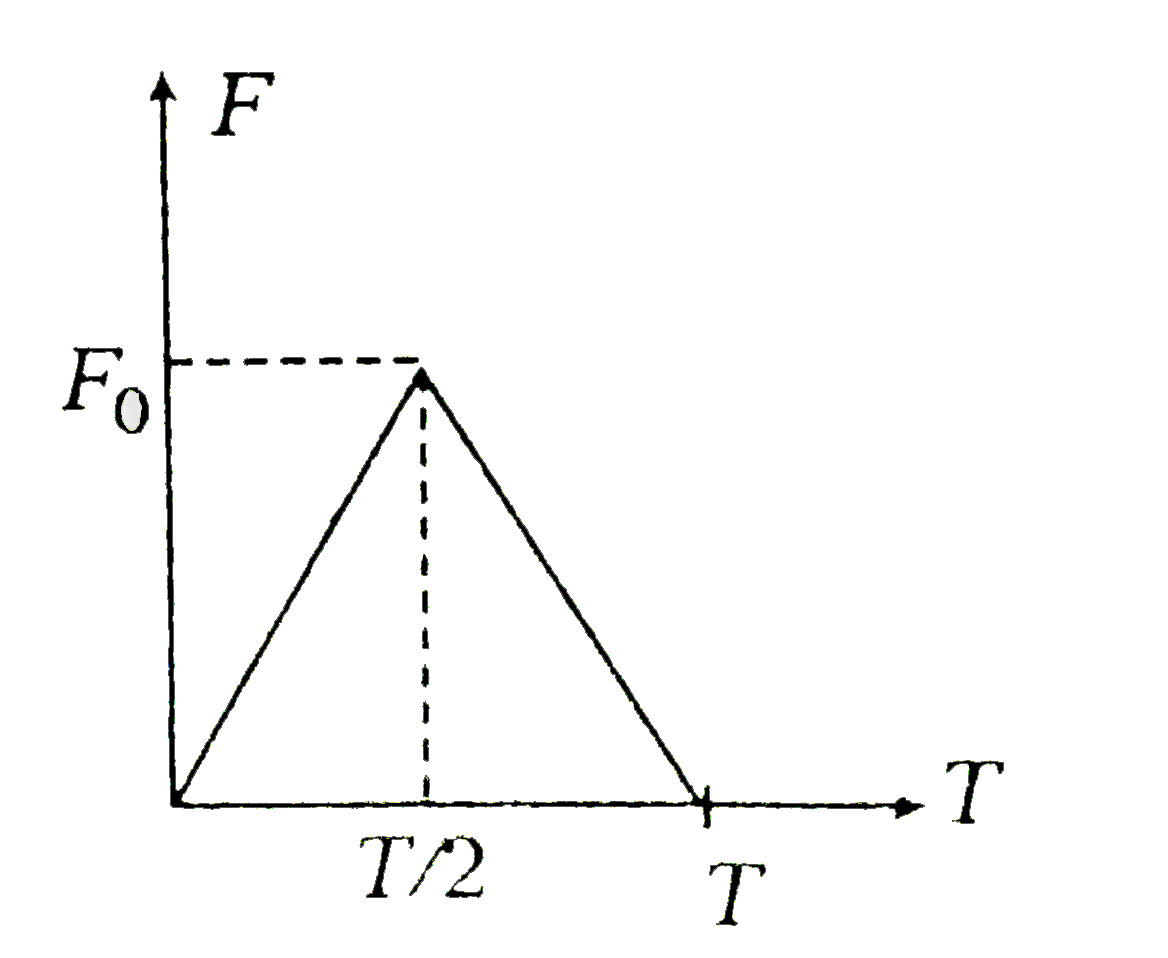
A particle of mass m moving with a velocity u makes an elastic one-dimensional collision with a stationary particle of mass m establishing a contact with it for extermely small time. T. Their force of contact increases from zero to F0 linearly in time T/4, remains constant for a further time T/2 and decreases linearly from F0 to zero in further time T/4 as shown. The magnitude possessed by F0 is.
 .AmuTB2muTC4mu3TD3mu4T
.AmuTB2muTC4mu3TD3mu4TA particle of mass m is moving along the line y-b with constant acceleration a. The areal velocity of the position vector of the particle at time t is (u=0)
AconstantBabt2Cabt2mDa2bt2mAt t=0 aparticle of mass m start moving from rest due to a force →F=F0sin(ωt)ˆi :
AParticle perform SHM about its initial position of restBParticle perform SHM with initial position as extreme position with angular frequency ωCAt any instant, distance moved by the particle equals its displacement, from the initial positionDinitial velocity of particle increases with time but after time t=2π/ω it becomes constant
A particle of mass m is moving with constant velocity v0 along the line y=b. At time t=0 it was at the point (0,b). At time t=bv0, the

View SolutionA particle of mass m moving with velocity v0 collides with sphere of same mass at rest , as shown. If the surface of contact is smooth and the collision is elastic, find the velocities of particle and sphere after the collision.

View SolutionFind the time t0 when x-coordinate of the particle is zero.
View SolutionThe velocity of a particle is zero at t=0
View SolutionA particle of rest mass m0 starts moving at a moment t=0 due to a constant force F. Find the time dependence of the particle's velocity and of the distance covered.
View Solution

