Question

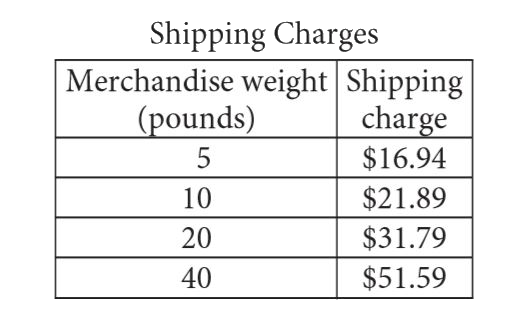
The table above shows shipping charges for an online retailer that sells sporting goods. There is a linear relationship between the shipping charge and the weight of the merchandise. Which function can be used to determine the total shipping charge f (x) , in dollars, for an order with a merchandise weight of x pounds?

Options

A. f (x) = 0.99x
B. f (x) = 0.99x + 11.99
C. f (x) = 3.39x
D. f (x) = 3.39x + 16.94

Answer

B

Explanation

Since the relationship between the merchandise weight x and the shipping charge f (x ) is linear, a function in the form f (x ) = mx + b, where m and b are constants, can be used. In this situation, the constant m represents the additional shipping charge, in dollars, for each additional pound of merchandise shipped, and the constant b represents a one-time charge, in dollars, for shipping any weight, in pounds, of merchandise. Using any two pairs of values from the table, such as (10, 21.89) and (20, 31.79), and dividing the difference in the charges by the difference in the weights gives the value of m: `m=(31.79-21.89)/(20-10)` , which simplifies to `(9.9)/10` or , 0.99. Substituting the value of m and any pair of values from the table, such as (10, 21.89), for x and f (x ), respectively, gives the value of b: 21.89 = 0.99(10) + b, or b = 11.99. Therefore, the function f (x ) = 0.99x + 11.99 can be used to determine the total shipping charge f (x ), in dollars, for an order with a merchandise weight of x pounds.
Choices A, C, and D are incorrect. If any pair of values from the table is substituted for x and f (x ), respectively, in these functions, the result is false. For example, substituting 10 for x and 21.89 for f (x ) in f (x ) = 0.99x yields 21.89 = 0.99(10), or 21.89 = 9.9, which is false. Similarly, substituting the values (10, 21.89) for x and f (x ) into the functions in choices C and D results in 21.89 = 33.9 and 21.89 = 50.84, respectively. Both are false.