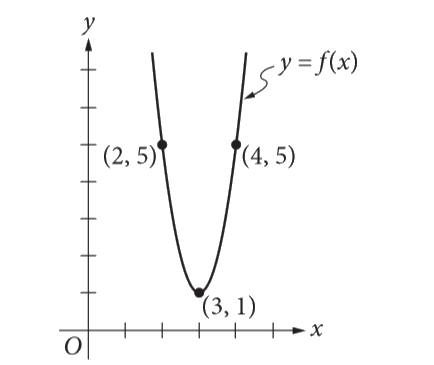
The graph of the function f in the xy-plane above is a parabola. Which of the following defines f ?
f(x)=4(x−3)2+1
f(x)=4(x+3)2+1
f(x)=(x−3)2+1
f(x)=3(x+3)2+1
The correct Answer is:A
The equation of a parabola in vertex form is f(x)=a(x−h)2+k, where the point (h, k) is the vertex of the parabola and a is a constant. The graph shows that the coordinates of the vertex are (3, 1), so h = 3 and k = 1. Therefore, an equation that defines f can be written as f(x)=a(x−3)2+1. To find a, substitute a value for x and its corresponding value for y, or f(x). For example, (4, 5) is a point on the graph of f. So a must satisfy the equation5=a(4−3)2+1, which can be rewritten as 4=a(1)2, or a = 4. An equation that defines f is therefore f(x)=4(x−3)2+1.
Choice B is incorrect and may result from a sign error when writing the equation of the parabola in vertex form. Choice C is incorrect and may result from omitting the constant a from the vertex form of the equation of the parabola. Choice D is incorrect and may result from a sign error when writing the equation of the parabola in vertex form as well as by miscalculating the value of a.
Similar Questions
The inequation represented by the graph given below is :
View SolutionThe inequation that best describes the graph given below is _________
View SolutionThe inequation that best describes the following graph is _________
View SolutionWhich inequations represent the shaded region in the given figure
View SolutionFrom the following figure, the correct observation is :- ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/ALN_PHY_R03_E08_015_Q01.png" width="80%"gt
View SolutionMatch the followings (column I with column II)
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/NCERT_BIO_XI_C03_E01_011_Q01.png" width="80%"gt
View SolutionMatch the following:
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/NCERT_BIO_XI_C04_E01_014_Q01.png" width="80%"gt
View SolutionMatch the following : ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/NCERT_BIO_XI_C22_E09_Q01.png" width="80%"gt
View Solution