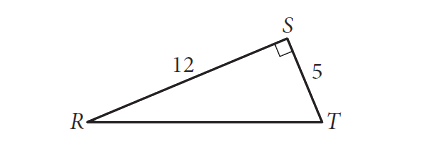
In triangle RST above, point W (not shown) lies on . What is the value of cos( ?
Video Solution
Text Solution
The correct Answer is:0
Note that no matter where point W is on , the sum of the measures of and is equal to the measure of , which is . Thus, and are complementary angles. Since the cosine of an angle is equal to the sine of its complementary angle, . Therefore,
|
Similar Questions
Knowledge Check
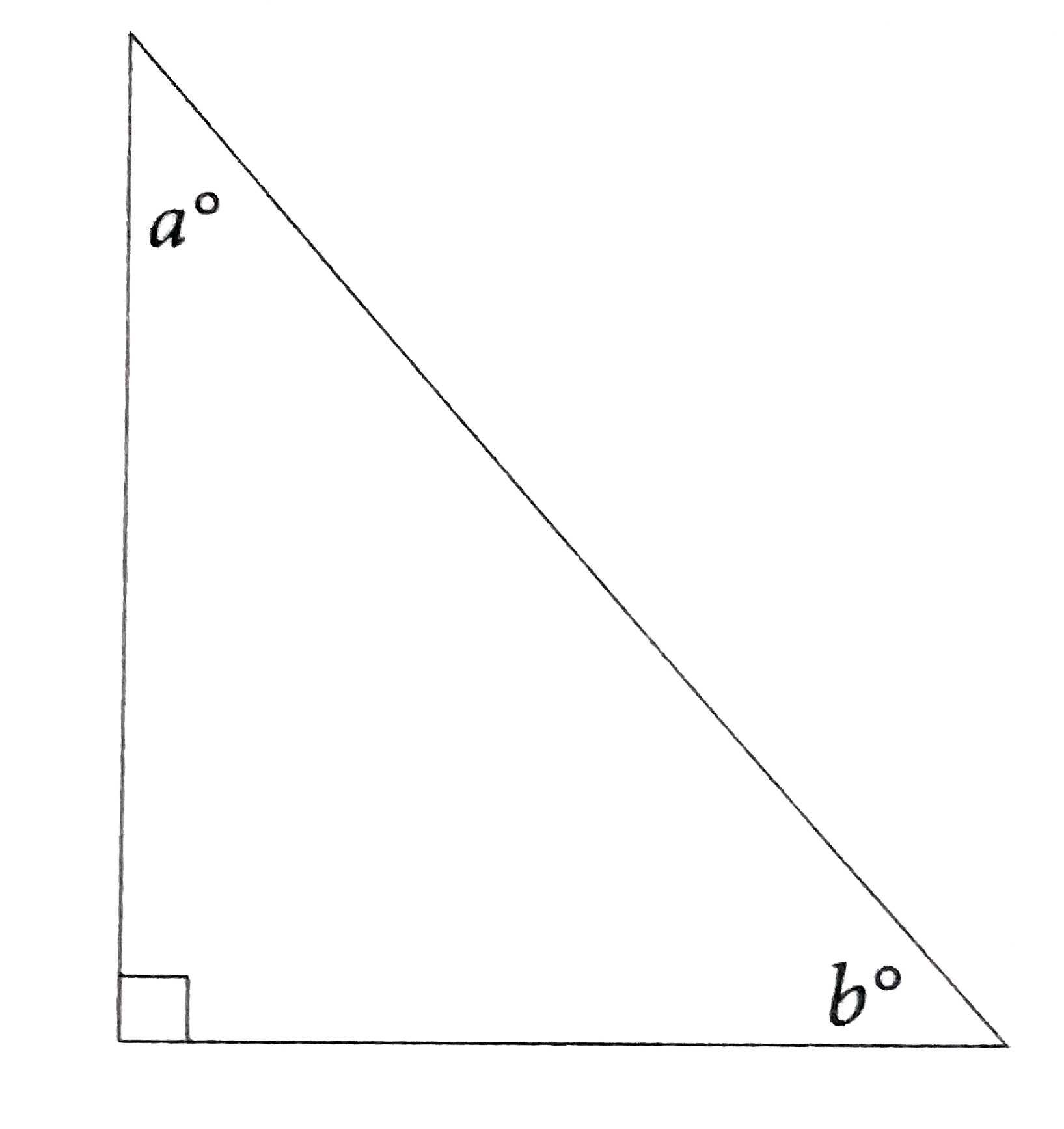
In the figure above, sin a=x what is the value of cos b?AxB1xC|1−x|D90−x90The coordinates of the vertices of ΔMON are shown in the standard ( x,y) coordination plane below . Rectangle MPQR is shown shaded . Point P lies on ¯¯¯¯¯¯¯MO, point Q lies on ¯¯¯¯¯¯¯¯MN
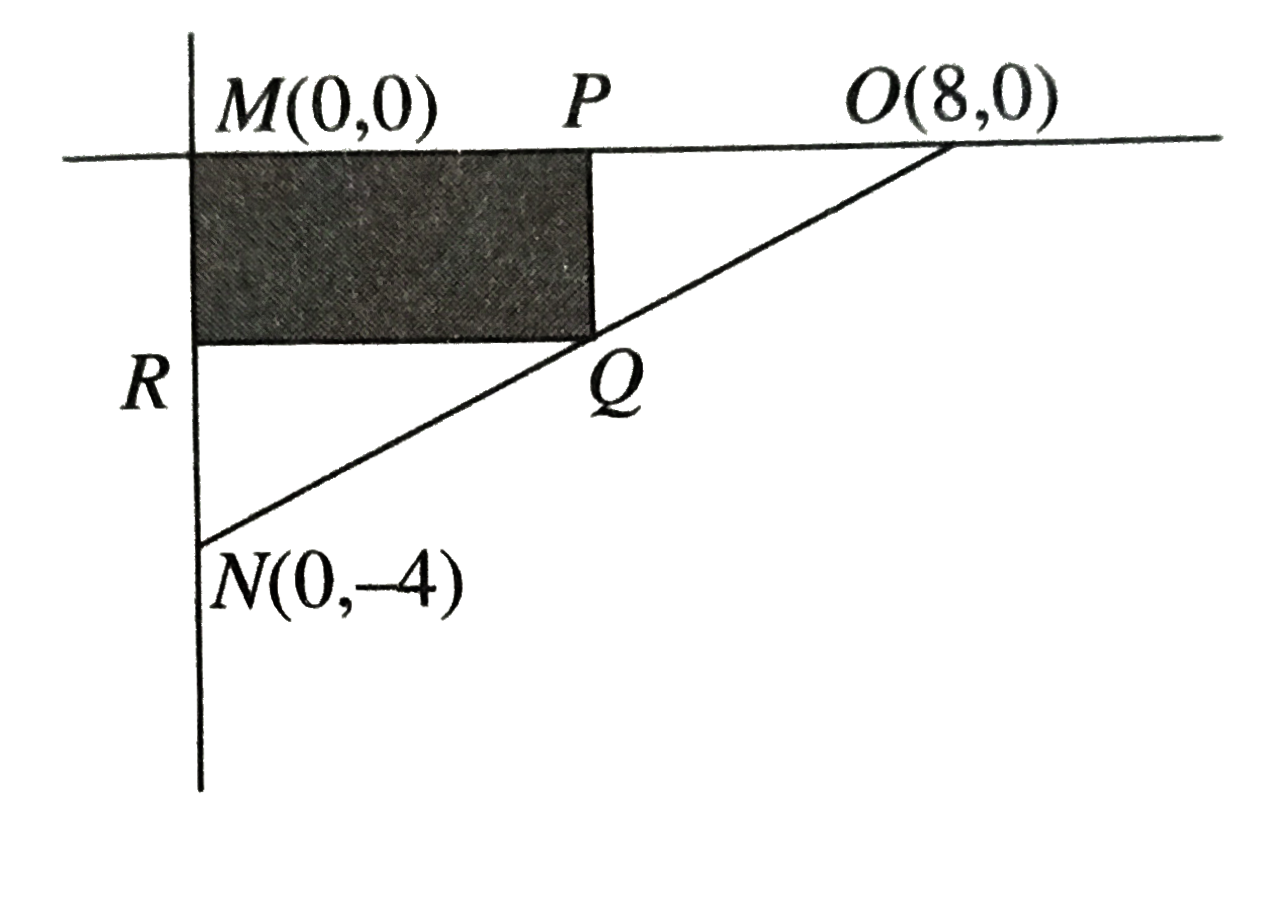
What is the value of cos(∠MON) ?A4√80B8√80C12D2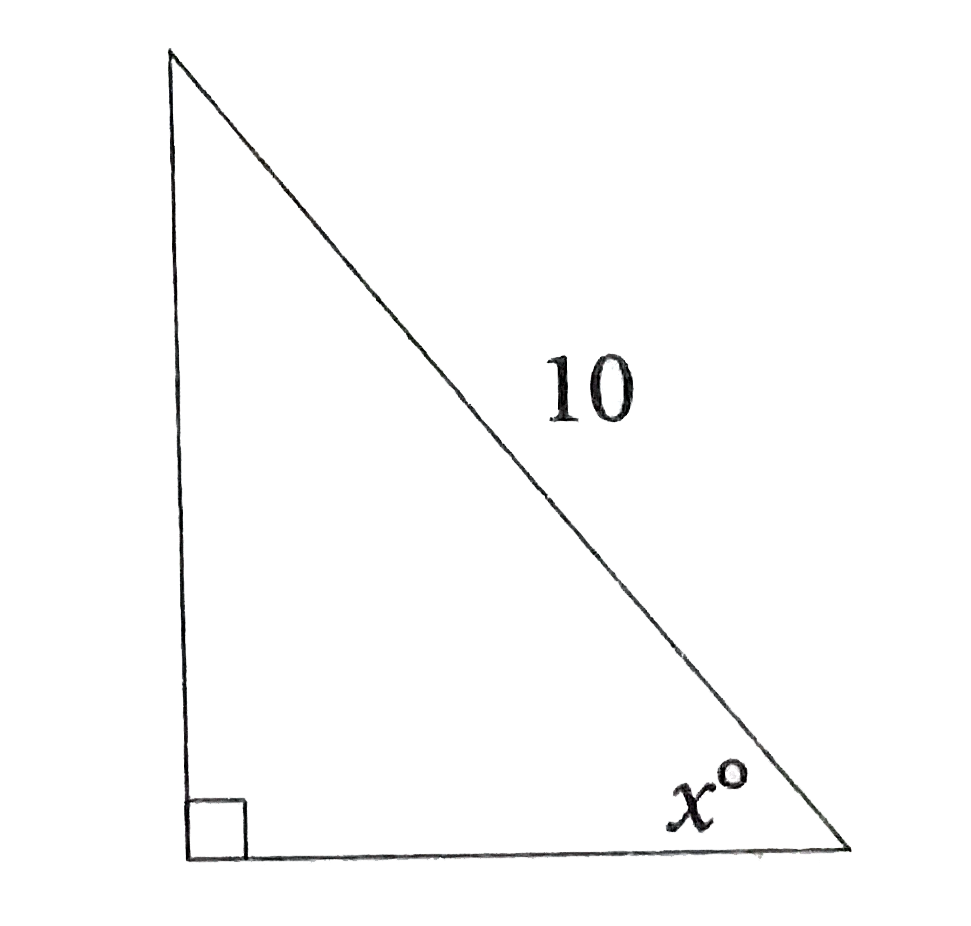
In the triangle above, sin x=0.8 and cos x=0.6. What is the area of the triangle?A0.48B4.8C24D48

On the number above. What is the value of point x?
View Solution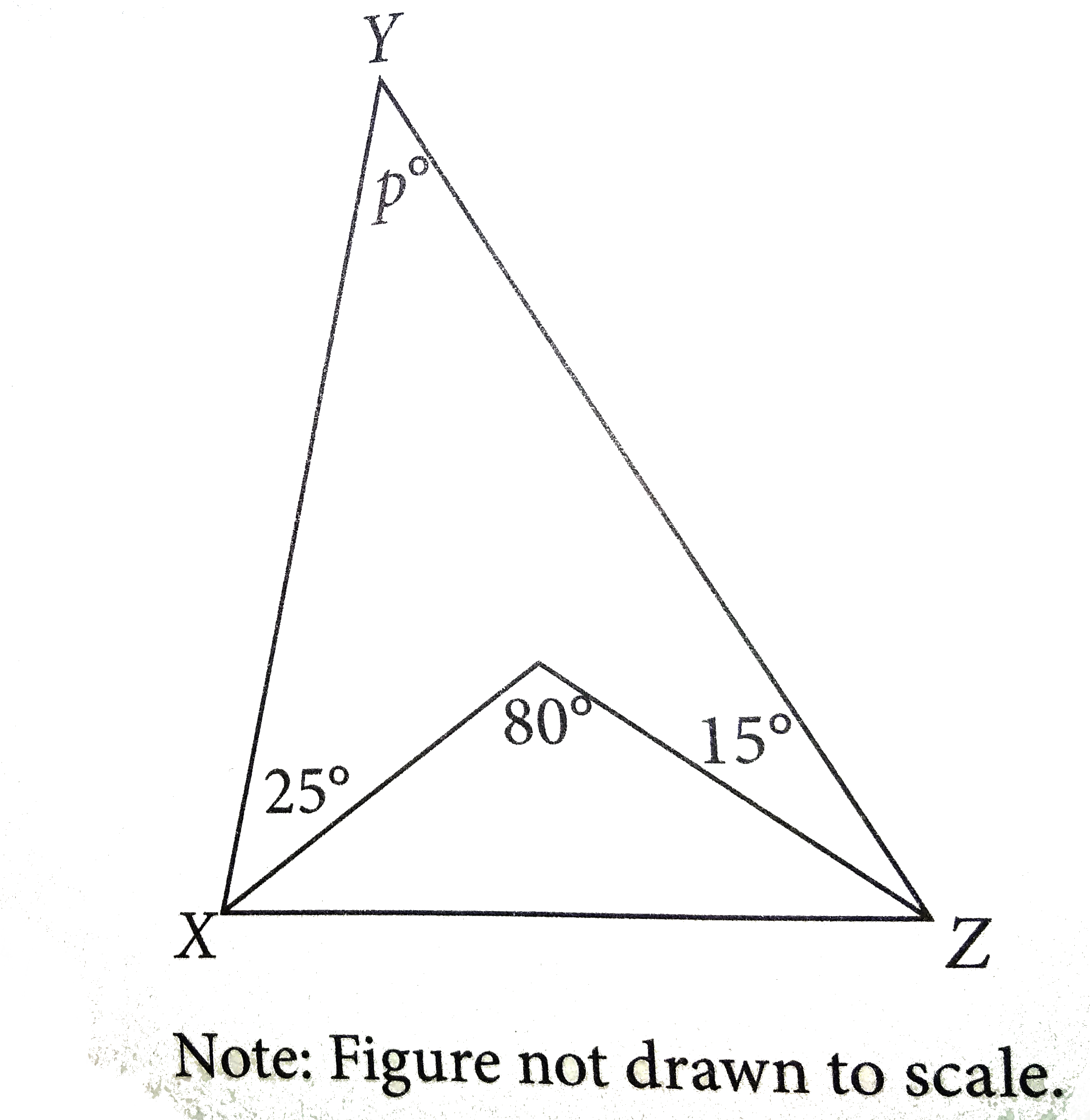
In triangle XYZ above, what is the value of p?
View Solution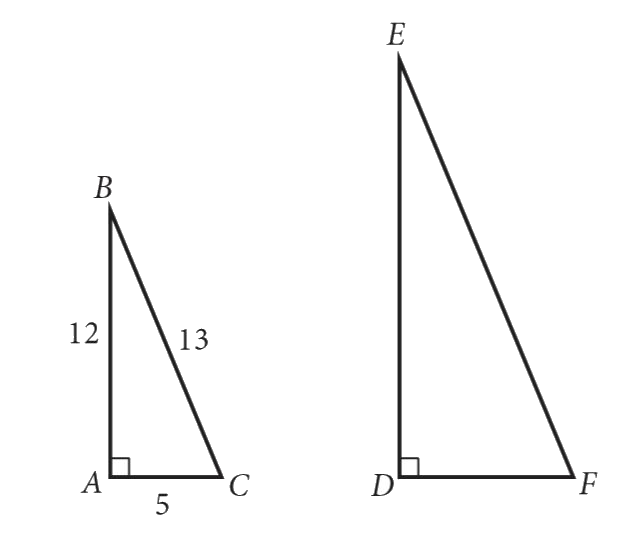
In the figure above, triangle ABC is similar to triangle DEF . What is the value of cos(E) ?
View Solution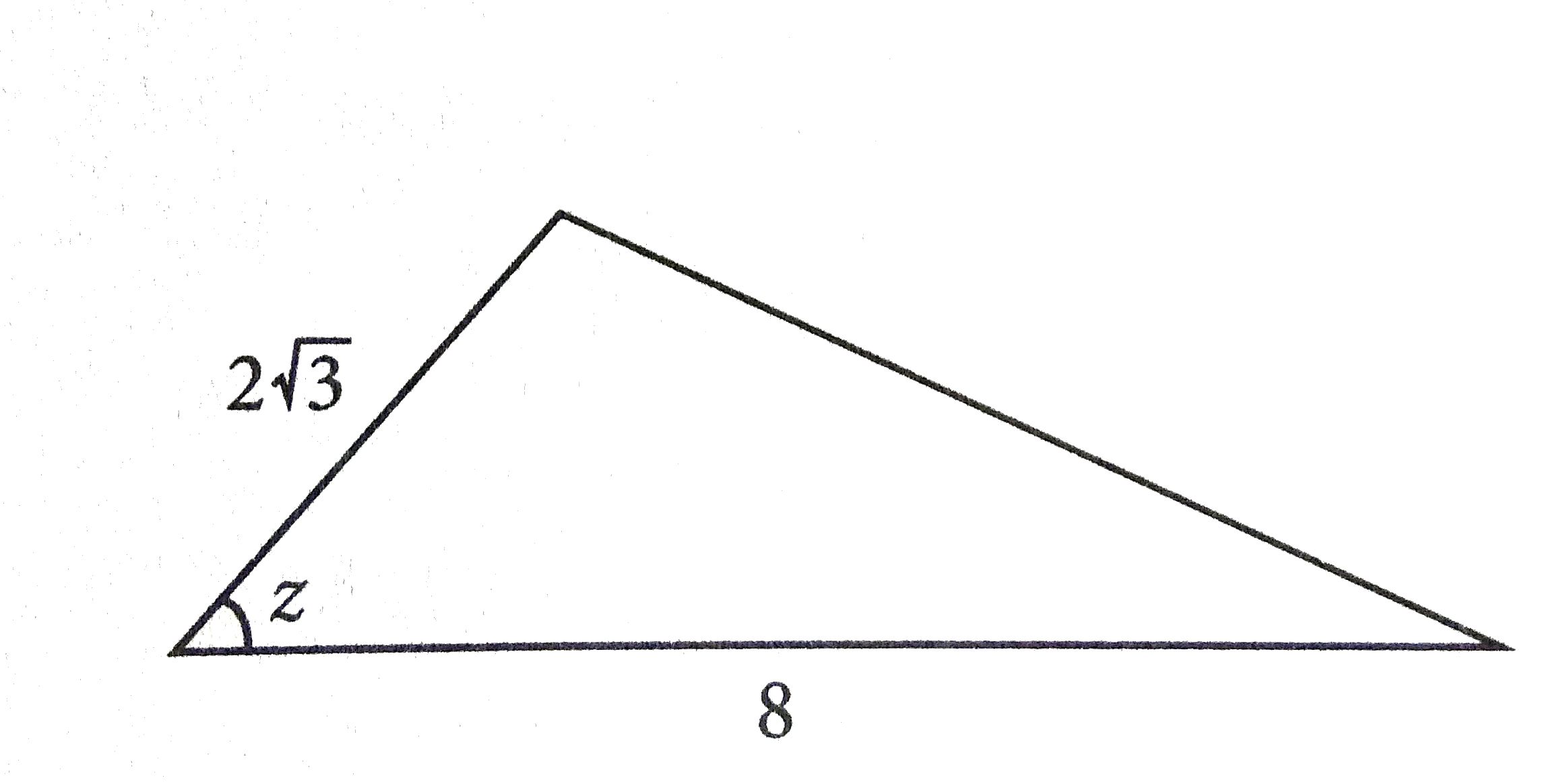
If the area of the triangle shown above is 12 squares inches, what is the value of cosz?
View Solution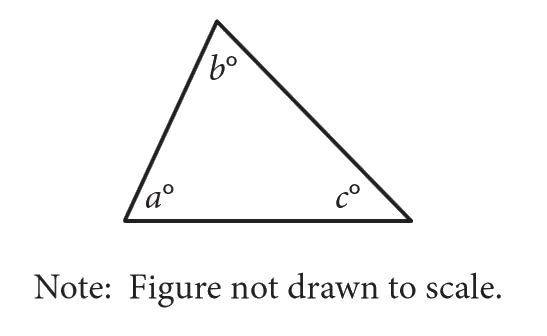
In the triangle above, a = 34 . What is the value of b + c ?
View Solution