Question

Population of Greenleaf, Idaho

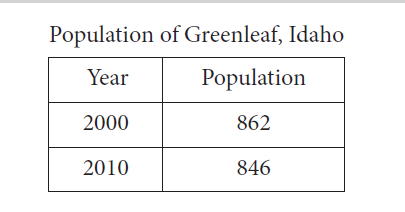
The table above shows the population of Greenleaf, Idaho, for the years 2000 and 2010. If the relationship between population and year is linear, which of the following functions P models the population of Greenleaf t years after 2000?

Options

A. P(t) = 862 − 1.6t
B. P(t) = 862 − 16t
C. P(t) = 862 + 16(t − 2,000)
D. P(t) = 862 − 1.6(t − 2,000)

Answer

A

Explanation

It is given that the relationship between population and year is linear, therefore, the function that models the population t years after 2000 is of the form P (t) = mt + b, where m is the slope and b is the population when t = 0. In the year 2000, t = 0. Therefore, b = 862. The slope is given by `m=(P(10)-P(0))/(10-0)=(846-862)/(10-0)=(-16)/10=-1.6`. Therefore ,P(t)=-1.6t+862, which is equivalent to the equation in choice A.
Choice B is incorrect and may be the result of incorrectly calculating the slope as just the change in the value of P. Choice C is incorrect and may be the result of the same error as in choice B, in addition to incorrectly using t to represent the year, instead of the number of years after 2000. Choice D is incorrect and may be the result of incorrectly using t to represent the year instead of the number of years after 2000.