Roberto is an insurance agent who sells two types of policies: a $50,000 policy and a $100,000 policy. Last month, his goal was to sell at least 57 insurance policies. While he did not meet his goal, the total value of the policies he sold was over $3,000,000. Which of the following systems of inequalities describes x, the possible number of $50,000 policies, and y, the possible number of $100,000 policies, that Roberto sold last month?
x+y lt 57
50,000x + 100,000y lt 3,000,000
x+y gt 57
50,000x +100,000y gt 3,000,000
x+ylt57
50,000x + 100,000 y gt 3,000,000
x+ygt57
50,000x + 100,000y lt 3,000,000
The correct Answer is:C
To solve the problem, we need to set up a system of inequalities based on the information provided about Roberto's insurance policies.
1. Identify Variables:
- Let x be the number of $50,000 policies sold.
- Let y be the number of $100,000 policies sold.
2. Total Policies Sold:
- Roberto's goal was to sell at least 57 policies, but he did not meet this goal. This means:
x+y<57
3. Total Value of Policies Sold:
- The total value of the policies sold was over $3,000,000. The value from $50,000 policies is 50,000x and from $100,000 policies is 100,000y. Therefore, we can express this as:
50,000x+100,000y>3,000,000
4. Final System of Inequalities:
- Combining the two inequalities, we have:
{x+y<5750,000x+100,000y>3,000,000
5. Identify the Correct Option:
- From the options provided, we see that option 3 matches our derived inequalities:
- x+y<57
- 50,000x+100,000y>3,000,000
Thus, the correct system of inequalities that describes the possible number of $50,000 policies (x) and $100,000 policies (y) that Roberto sold last month is:
{x+y<5750,000x+100,000y>3,000,000
- Let x be the number of $50,000 policies sold.
- Let y be the number of $100,000 policies sold.
- Roberto's goal was to sell at least 57 policies, but he did not meet this goal. This means:
x+y<57
- The total value of the policies sold was over $3,000,000. The value from $50,000 policies is 50,000x and from $100,000 policies is 100,000y. Therefore, we can express this as:
50,000x+100,000y>3,000,000
- Combining the two inequalities, we have:
{x+y<5750,000x+100,000y>3,000,000
- From the options provided, we see that option 3 matches our derived inequalities:
- x+y<57
- 50,000x+100,000y>3,000,000
{x+y<5750,000x+100,000y>3,000,000
Similar Questions
What was the slogan coined by Hitler when he followed his aggressive policy ?
View SolutionHe said, "Honesty is the best policy."
View SolutionThe period for the fire insurance policy is
View SolutionState True or False: The value of insured property is called policy value
View SolutionIn this question, sentence is given with blank to be filled in with an appropriate word. Four alternatives are suggested for question. Choose the correct alternative out of the four.
When he got married he _______ a life insurance policy.
View SolutionA life insurance agent found the following data for distribution of ages of 100 policy holders. A policy holder is chosen at random.
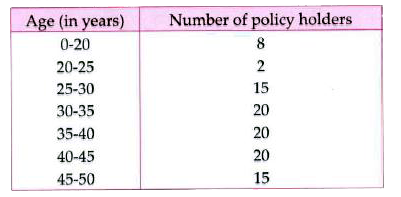
Find the sum of probabilities if a policy holder are chosen randomly of age (0-20) years and policy holders of age (25-30) years
View SolutionA life insurance agent found the following data for distribution of ages of 100 policy holders. A policy holder is chosen at random.

Probability of policy holders chosen randomly of age less than 25 years is
View SolutionWhile trying to promote growth by tax cuts as the fiscal policy, which type of policy is the government trying to follow ?
View Solution
