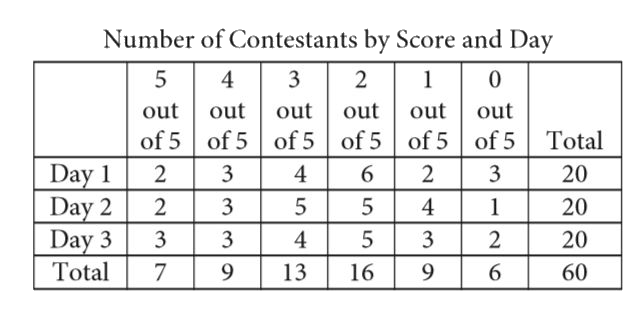
The same 20 contestants, on each of 3 days, answered 5 questions in order to win a prize. Each contestant received 1 point for each correct answer. The number of contestants receiving a given score on each day is shown in the table above.
What was the mean score of the contestants on Day 1 ?
The correct Answer is:B, D
The mean score of the 20 contestants on Day 1 is found by dividing the sum of the total scores of the contestants by the number of contestants. It is given that each contestant received 1 point for each correct answer. The table shows that on Day 1, 2 contestants each answered 5 questions correctly, so those 2 contestants scored 10 points in total (2 × 5 = 10). Similarly, the table shows 3 contestants each answered 4 questions correctly, so those 3 contestants scored 12 points in total (3 × 4 = 12). Continuing these calculations reveals that the 4 contestants who answered 3 questions correctly scored 12 points in total (4 × 3 = 12), the 6 contestants who answered 2 questions correctly scored 12 points in total (6 × 2 = 12), the 2 contestants who answered 1 question correctly scored 2 points in total (2 × 1 = 2), and the 3 contestants who answered 0 questions correctly scored 0 points in total (3 × 0 = 0). Adding up the total of points scored by these 20 contestants gives 10 + 12 + 12 + 12 + 2 + 0 = 48. Therefore, the mean score of the contestants is 4820 = 2.4. Either 12/5, 2.4, or 2.40 can be gridded as the correct answer.
Similar Questions
The inequation represented by the graph given below is :
02:10View SolutionThe inequation that best describes the graph given below is _________
02:17View SolutionThe inequation that best describes the following graph is _________
02:10View Solution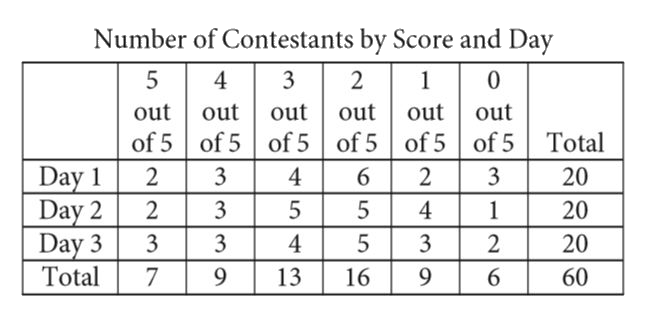
The same 20 contestants, on each of 3 days, answered 5 questions in order to win a prize. Each contestant received 1 point for each correct answer. The number of contestants receiving a given score on each day is shown in the table above.
No contestant received the same score on two different days. If a contestant is selected at random, what is the probability that the selected contestant received a score of 5 on Day 2 or Day 3, given that the contestant received a score of 5 on one of the three days?03:20View Solution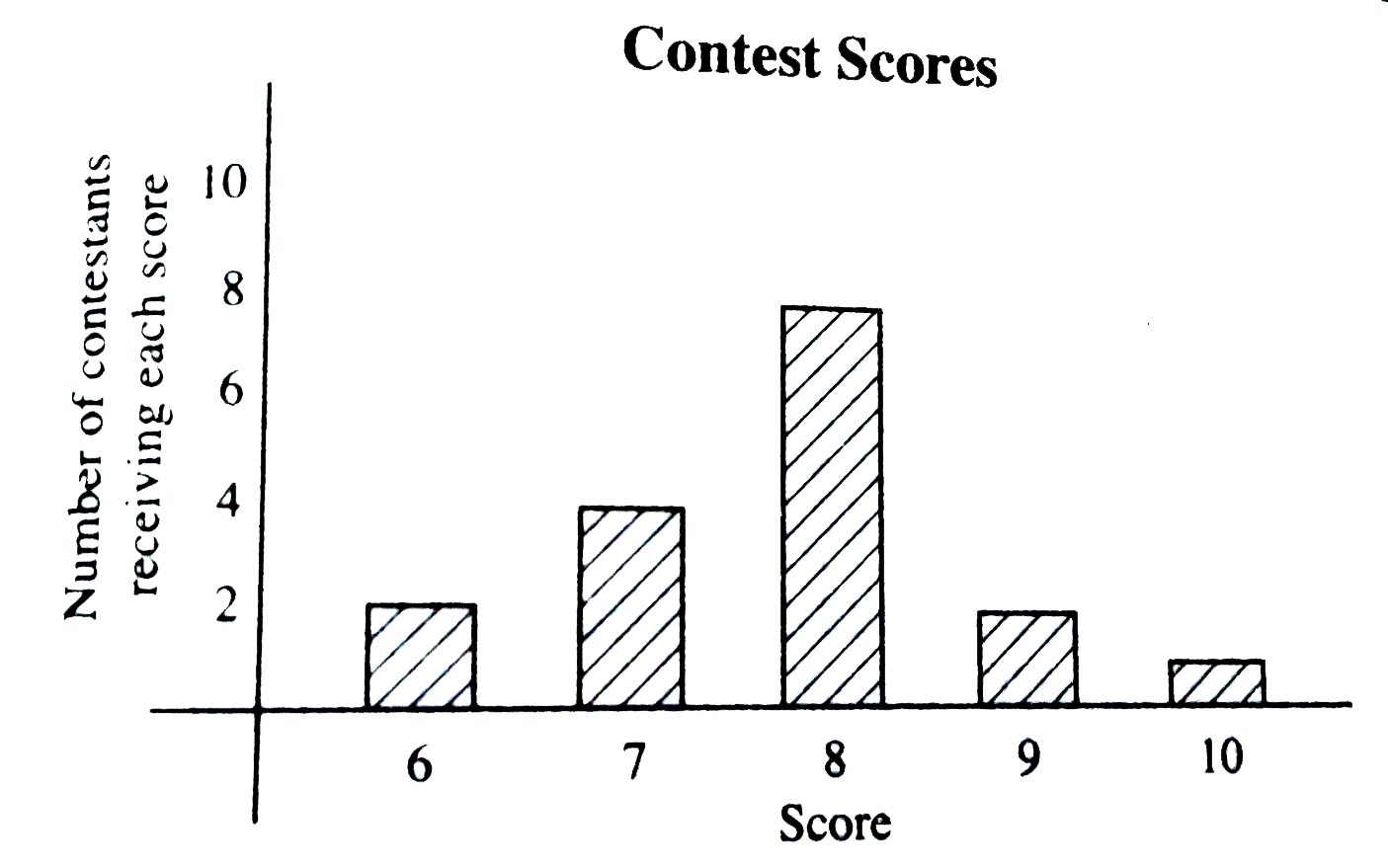
In a contest , each contestant could receive a score of 6,7,8,9, or 10. The bar graph above shows how many contestants received each score .
The score of 8 is described by which of the following measures ?
I.The average (arithmetic mean )
II.The median
III.The mode03:43View Solution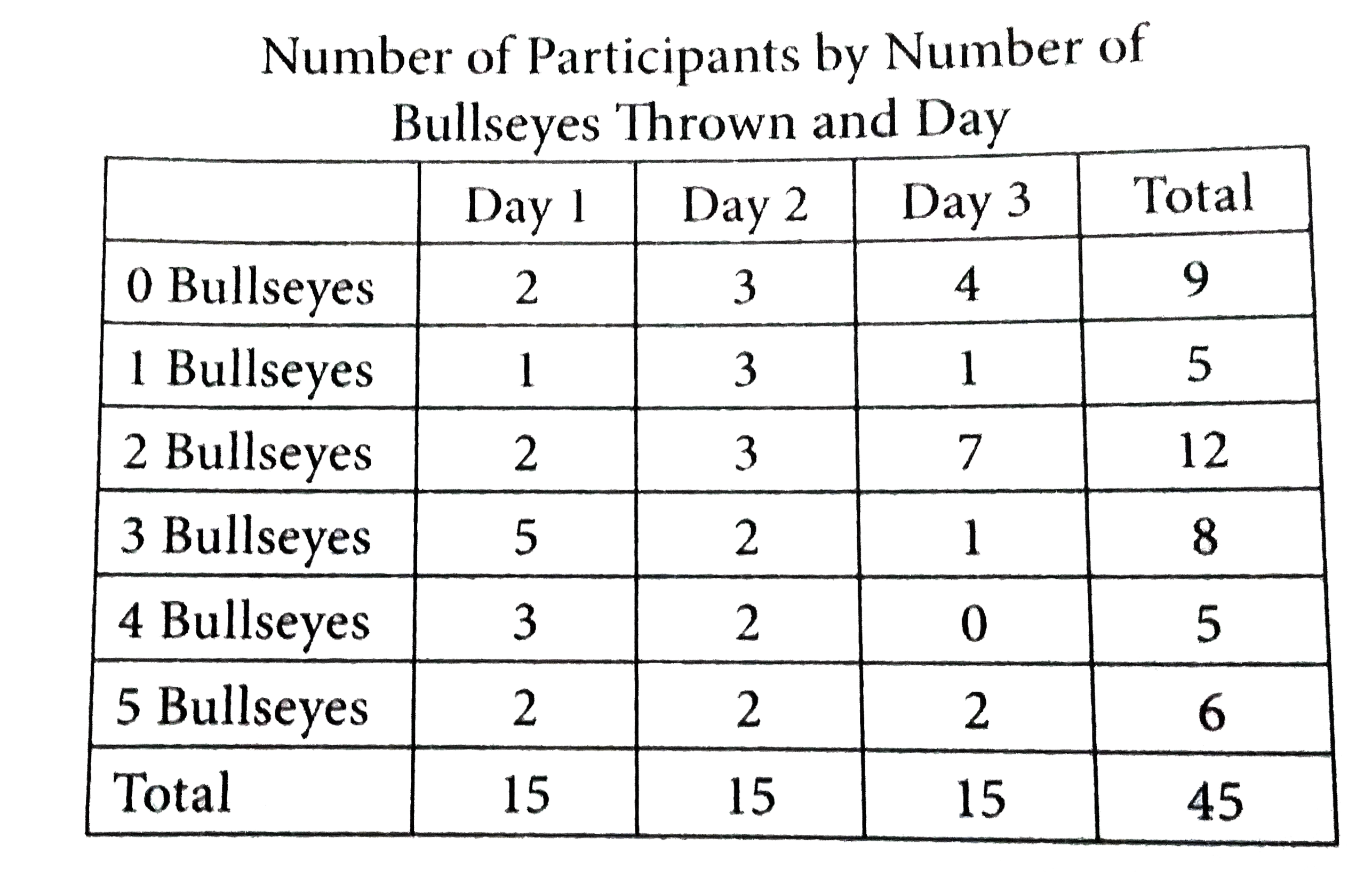
The same 15 participants, on each of 3 days, threw 5 darts in order to win a bullseye contest. The number of players throwing a given number of bullseyes on each day is shown in the table above.
No Participant threw the same number of bullseyes on two different days. IF a participant is selected at random, what is the probability that the selected participant threw 3 bullseyes on Day 1 or DAY2, given that the contestant threw 3 bullseyes on one of the three days?View Solution
The same 15 participants, on each of 3 days, threw 5 darts in order to win a bullseye contest. The number of players throwing a given number of bullseyes on each day is shown in the table above.
What is the mean number of bullseyes each participant threw on DAY 2?View Solution

