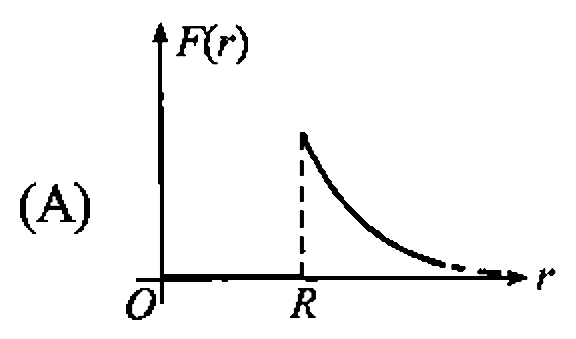
A particle of mass m is ocated at a distance r from the centre of shell of mass M and radius R. The force between the shell and mass F(r). The plot of F(r) ve r is :
The correct Answer is:A
To solve the problem, we need to analyze the gravitational force between a particle of mass m located at a distance r from the center of a spherical shell of mass M and radius R. We will consider two cases: when the particle is inside the shell and when it is outside the shell.
Step 1: Analyze the Case When r<R (Inside the Shell)
- According to the shell theorem, the gravitational force inside a uniform spherical shell is zero. This means that if the particle of mass m is located anywhere inside the shell (i.e., r<R), the gravitational force F(r) acting on it due to the shell is:
F(r)=0for r<R
Step 2: Analyze the Case When r≥R (Outside the Shell)
- When the particle is outside the shell (i.e., r≥R), the entire mass of the shell can be treated as if it were concentrated at its center. The gravitational force F(r) acting on the particle is given by Newton's law of gravitation:
F(r)=GMmr2
where G is the gravitational constant.
Step 3: Combine the Results
- We can summarize the results as follows:
- For r<R: F(r)=0
- For r≥R: F(r)=GMmr2
Step 4: Plotting the Graph
- The graph of F(r) versus r will have two distinct regions:
- For r<R, the force F(r) is zero, which means the graph will be a horizontal line along the F-axis at F=0.
- For r≥R, the force F(r) decreases with r2, which means the graph will show a hyperbolic decline as r increases.
Conclusion
- The plot of F(r) versus r will look like this:
- A horizontal line at F=0 for r<R
- A curve that decreases as r increases for r≥R
Final Answer
The correct option for the plot of F(r) versus r is option A.
---
- According to the shell theorem, the gravitational force inside a uniform spherical shell is zero. This means that if the particle of mass m is located anywhere inside the shell (i.e., r<R), the gravitational force F(r) acting on it due to the shell is:
F(r)=0for r<R
- When the particle is outside the shell (i.e., r≥R), the entire mass of the shell can be treated as if it were concentrated at its center. The gravitational force F(r) acting on the particle is given by Newton's law of gravitation:
F(r)=GMmr2
where G is the gravitational constant.
- We can summarize the results as follows:
- For r<R: F(r)=0
- For r≥R: F(r)=GMmr2
- The graph of F(r) versus r will have two distinct regions:
- For r<R, the force F(r) is zero, which means the graph will be a horizontal line along the F-axis at F=0.
- For r≥R, the force F(r) decreases with r2, which means the graph will show a hyperbolic decline as r increases.
- The plot of F(r) versus r will look like this:
- A horizontal line at F=0 for r<R
- A curve that decreases as r increases for r≥R
The correct option for the plot of F(r) versus r is option A.
Topper's Solved these Questions
- GRAVITATIONBook:PHYSICS GALAXY - ASHISH ARORAChapter:GRAVITATIONExercise:Numerial MCQs
Explore 59 Videos
- GRAVITATIONBook:PHYSICS GALAXY - ASHISH ARORAChapter:GRAVITATIONExercise:Advance MCQs
Explore 17 Videos
- GRAVITATIONBook:PHYSICS GALAXY - ASHISH ARORAChapter:GRAVITATIONExercise:Discussion Qns
Explore 31 Videos
- FLUID MECHANICSBook:PHYSICS GALAXY - ASHISH ARORAChapter:FLUID MECHANICSExercise:Unsolved Numerical Problems
Explore 86 Videos
- KINEMATICSBook:PHYSICS GALAXY - ASHISH ARORAChapter:KINEMATICSExercise:Unsolved Numerical Pro.
Explore 83 Videos
Similar Questions
A point mass m is a distance x from the centre of mass M and radius R on its axis. Find the gravitational force between the two. What will this force be if x>>R and x<<R? For what value of x is the force maximum?
View SolutionA particle of mass m lies at a distance r from the centre of earth. The force of attraction between the particle and earth as a function of distance is F(r ),
View Solution
Knowledge Check
A block of mass m is lying at a distance r from a spherical shell of mass m and radius r, then :
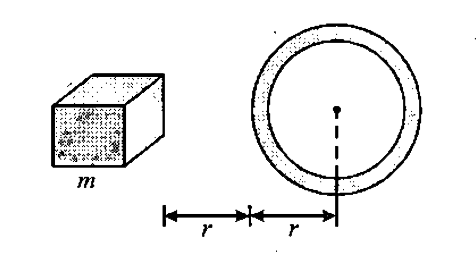 AOnly gravitational field inside the shell is zeroBGravitational field and gravitational potential both are zero inside the shellCGravitational potential as well as gravitational field inside the shell are not zeroDCan't be ascertained.
AOnly gravitational field inside the shell is zeroBGravitational field and gravitational potential both are zero inside the shellCGravitational potential as well as gravitational field inside the shell are not zeroDCan't be ascertained.A particle of mass m is located inside a spherical shell of mass M and radius R. The gravitational force of attraction between them is
AGMmRBGMmR2C−GMmR2D0A point mass m0 is placed at distance R/3 from the centre of spherical shell of mass m and radius R. the gravitational force on the point mass m0 is
A4Gmm0R2BzeroC9Gmm0R2DNone of these
P is a point at a distance r from the centre of a spherical shell of mass M and radius a, where r<a. The gravitational potential at P is
View SolutionA particle at a distance r from the centre of a uniform spherical planet of mass M radius R (ltr) has a velocity of magnitude v.
View SolutionA particel of mass M is placed at the centre of a inform spherical shell of mass 2M and radius R. The gravitational potential on the surface of the shell is
View SolutionThe distance of the centre of mass of a hemispherical shell of radius R from its centre is
View SolutionA particle of mass m is placed at the centre of a unifrom spherical shell of mass 3 m and radius R The gravitational potential on the surface of the shell is .
View Solution

