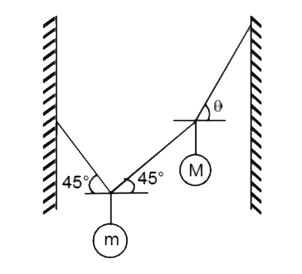
Two bodies of mass m and 4m are attached by a string shown in the figure-2.146. The body of mass m hanging from a string of length l is executing simple harmonic motion with amplitude A while other body is at rest on the surface. The minimum coefficient of friction between the mass 4m and the horizontal surface must be to keep it at rest is :

14(1−A2l2)
14(1+A2l2)
14Alcosθ
14
The correct Answer is:B
Step by step video, text & image solution for Two bodies of mass m and 4m are attached by a string shown in the figure-2.146. The body of mass m hanging from a string of length l is executing simple harmonic motion with amplitude A while other body is at rest on the surface. The minimum coefficient of friction between the mass 4m and the horizontal surface must be to keep it at rest is : by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- NEWTONS LAWS OF MOTIONBook:PHYSICS GALAXY - ASHISH ARORAChapter:NEWTONS LAWS OF MOTIONExercise:Advance MCQs
Explore 17 Videos
- NEWTONS LAWS OF MOTIONBook:PHYSICS GALAXY - ASHISH ARORAChapter:NEWTONS LAWS OF MOTIONExercise:Unsolved Numerical Problem
Explore 81 Videos
- NEWTONS LAWS OF MOTIONBook:PHYSICS GALAXY - ASHISH ARORAChapter:NEWTONS LAWS OF MOTIONExercise:Conceptual MCQs
Explore 23 Videos
- LINEAR MOMENTUM & ITS CONSERVATIONBook:PHYSICS GALAXY - ASHISH ARORAChapter:LINEAR MOMENTUM & ITS CONSERVATIONExercise:exercise 1.3
Explore 3 Videos
- RIGID BODIES AND ROTATIONAL MOTIONBook:PHYSICS GALAXY - ASHISH ARORAChapter:RIGID BODIES AND ROTATIONAL MOTIONExercise:Unsolved Numerical
Explore 63 Videos
Similar Questions
Knowledge Check
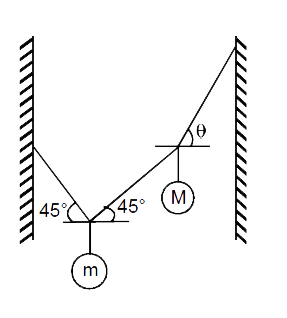
Two bodies of masses m and 4 m are attached with string as shown in the figure. The body of mass m hanging from a string of length l is executing oscillations of angular amplitude θ0 while the other body is at rest. The minimum coefficient of friction between the mass 4m and the horizontal surface should be
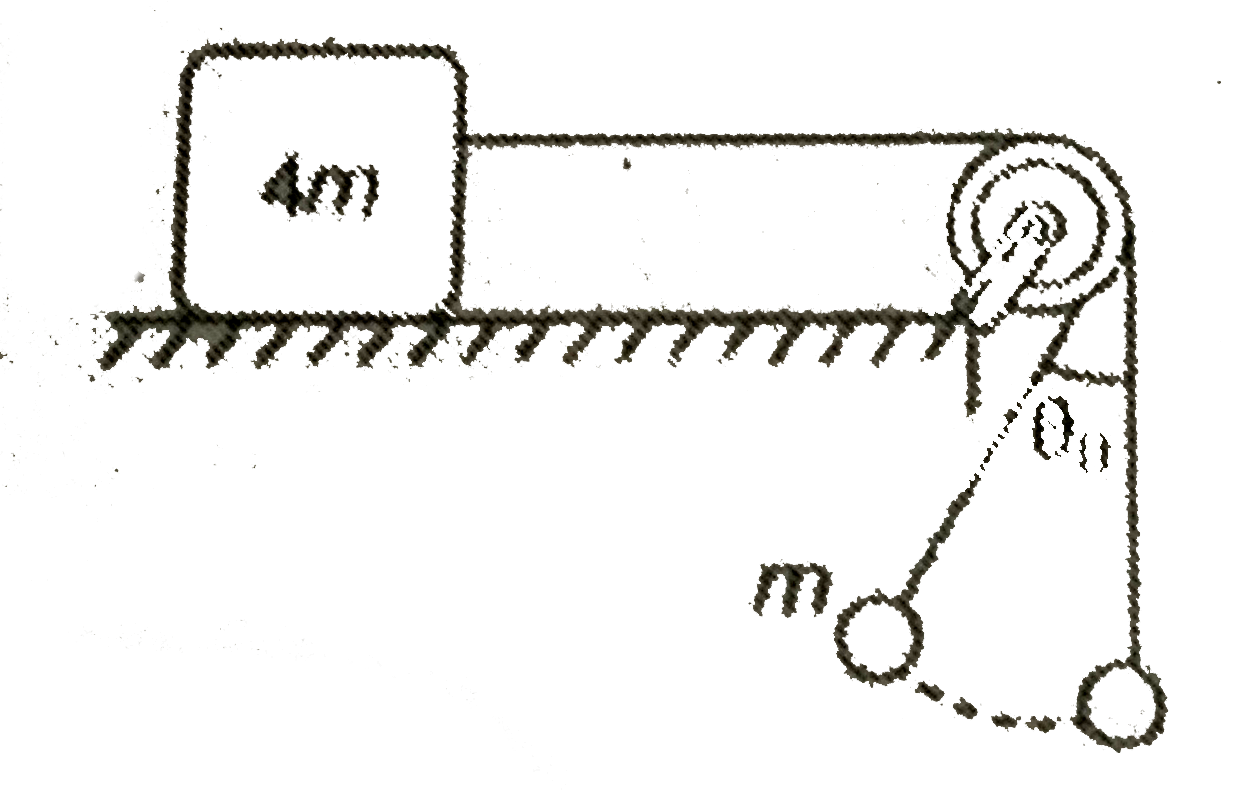 A(2−cosθ03)B2cos2(θ02)C(1−cosθ02)D(3−2cosθ04)
A(2−cosθ03)B2cos2(θ02)C(1−cosθ02)D(3−2cosθ04)Two bodies of masses m and 4m are attached to a light string as shown in figure. A body of mass m hanging from string is executing oscillations with angular amplitude 60∘, while other body is at rest on a horizontal surface. The minimum coefficient of friction between mass 4m and the horizontal surface is (here pulley is light and smooth)
 A(a) 14B(b) 34C(c) 12D(d) 18
A(a) 14B(b) 34C(c) 12D(d) 18Two bodies of mass m and 4m are attached with string of length l is excurting oscillations of angular amplitude θ0 while the other body is at rest . The minimum coefficient of friction between the mass 4m and the horizontal surface should be:
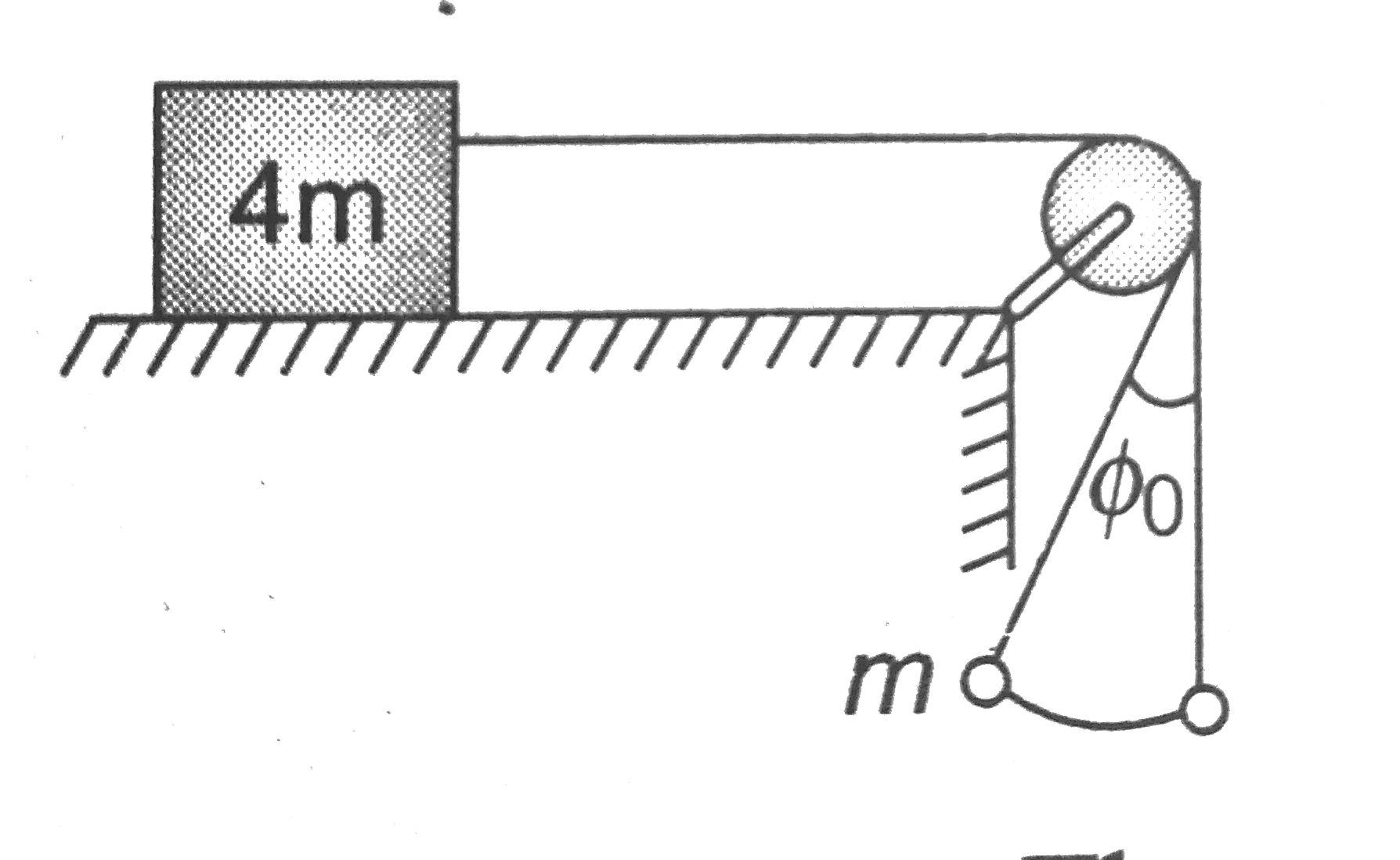 A(2−cosθ03)B2cos2(θ02)C(1−cosθ02)D(3−cosθ04)
A(2−cosθ03)B2cos2(θ02)C(1−cosθ02)D(3−cosθ04)
Find the minimum value of horizontal force (F) required on the block of mass m to keep it at rest on the wall. Given the coefficient of friction between the surfaces is μ.

View SolutionFind the mass M in the situation shown in figure-2.212 such that m remains at rest on the front surface of M1. The coefficient of friction between the front surface of M1 and that of m is μ.

View SolutionTwo masses m and M are attached to the strings as shown in the figure. If the system is in equilibrium, then
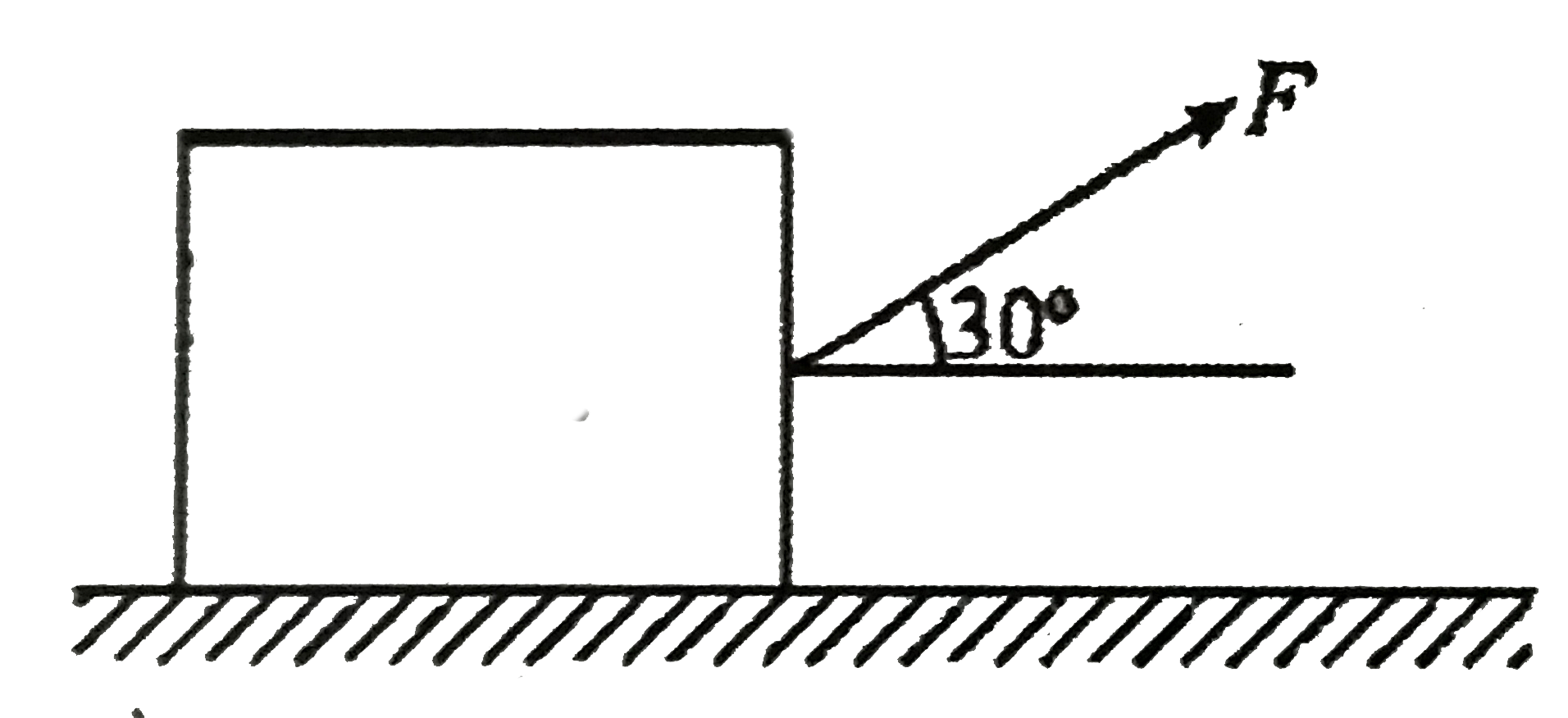
View SolutionA mass m rests under the action of a force F as shown in the figure-2.158 on a horizontal surface. The coefficient of friction between the mass and the surface is μ. The force of friction between the mass and the surface is :
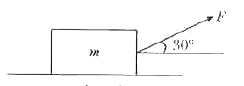
View SolutionA mass m is at rest under the action of a force F. as shown in the figure, on a horizontal surface. The coefficient of friction between mass and surface is u. Then, find the correct choice(s)
View Solution