Two cubes of masses and lie on two frictionless slopes of the block A which rests on horizontal table. The cubes are connected by a string, which passes over a pulley as shown in the figure-2.67. To what horizontal acceleration "f" the block accelerates so that the cubes do not slide down the planes ? What is the tension in the string in this situation ?
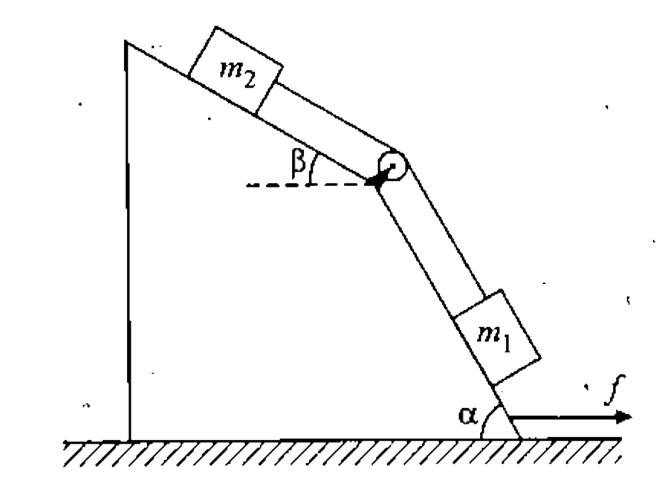
Step by step video & image solution for Two cubes of masses m_(1) and m_(2) lie on two frictionless slopes of the block A which rests on horizontal table. The cubes are connected by a string, which passes over a pulley as shown in the figure-2.67. To what horizontal acceleration "f" the block accelerates so that the cubes do not slide down the planes ? What is the tension in the string in this situation ? [f=g((m_(1)sinalpha+m_(2)sinbeta)/(m_(1)cosalpha+m_(2)cosbeta)),T = (m_(1)m_(2)gsin(alpha-beta))/(m_(1)cosalpha+m_(2)cosbeta)] by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- NEWTONS LAWS OF MOTIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Practice Exercise 2.2
1 Videos
- NEWTONS LAWS OF MOTIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Practice Exercise 2.3
1 Videos
- NEWTONS LAWS OF MOTIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Practice Exerice
4 Videos
- LINEAR MOMENTUM & ITS CONSERVATIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - LINEAR MOMENTUM & ITS CONSERVATIONEXERCISE - exercise 1.3
3 Videos
- RIGID BODIES AND ROTATIONAL MOTIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - RIGID BODIES AND ROTATIONAL MOTIONEXERCISE - Unsolved Numerical
63 Videos
Similar Questions
Two cubes of masses m1 and m2 be on two frictionless slopes of block A which rests on a horizontal table. The cubes are connected by a string which passes over a pulley as shown in figure. To what horizontal acceleration f should the whole system (that is blocks and cubes) be subjected so that the cubes do not slide down the planes. What is the tension of the string in this situation?
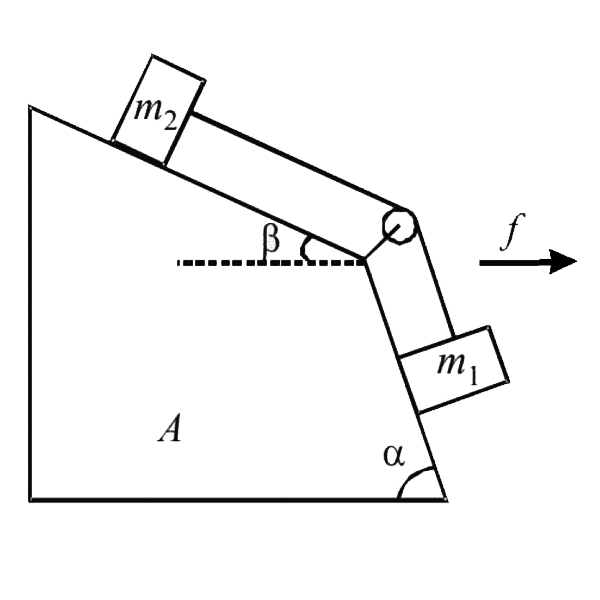
View SolutionTwo blocks are connected by a cord passing over a small frictionless pulley and resting on frictionless planes as shown in the figure. The acceleration of the blocks is :
View Solution
Knowledge Check
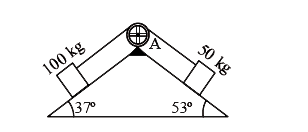
Two blocks of masses of 40 kg and 30 kg are connected by a weightless string passing over a frictionless pulley as shown in the figure.
 A0.7ms−2B0.8ms−2C0.6ms−2D0.5ms−2
A0.7ms−2B0.8ms−2C0.6ms−2D0.5ms−2Blocks of mass M1 and M2 are connected by a cord which passes over the pulleys P1 and P2 as shown in the figure. If there is no friction, the acceleration of the block of mass M2 will be
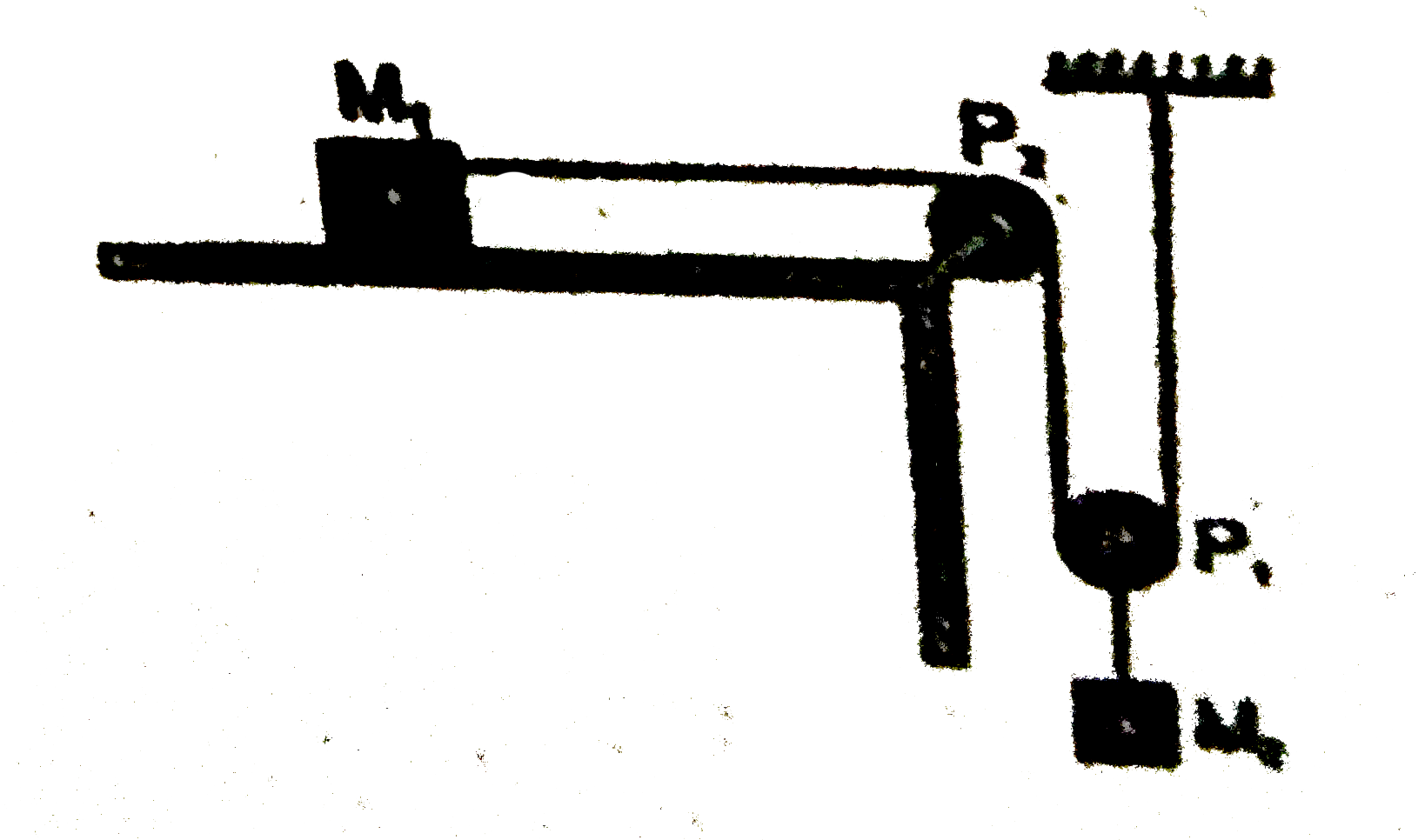 AM2g(4M1+M2)B2M2g(4M1+M2)C2M1g(M1+4M2)D2M1g(M1+M2)
AM2g(4M1+M2)B2M2g(4M1+M2)C2M1g(M1+4M2)D2M1g(M1+M2)
Two blocks of masses m1 and m2 are connected as shown in the figure. The acceleration of the block m2 is :Am2gm1+m2Bm1gm1+m2C4m2g−m1gm1+m2Dm2gm1+4m2
Two blocks A and B , each of mass 10kg , are connected by a light string passing over a smooth pulley as shown in the figure. Block A will remain at rest if the friction on it is

View SolutionTwo blocks of masses 3 kg and 6 kg are connected by a string as shown in the figure over a frictionless pulley. The acceleration of the system is

View SolutionTwo blocks, each having mass m, are connected with an ideal string through ideal pulleys on a frictionless fixed wedge as shown in the figure. The acceleration of the blocks is
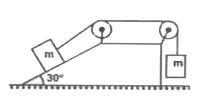
View SolutionTwo blocks are connected by a cord passing over a small frictionless pulley and resting on frictionless planes as shown in the figure The accleration of the blocks is-
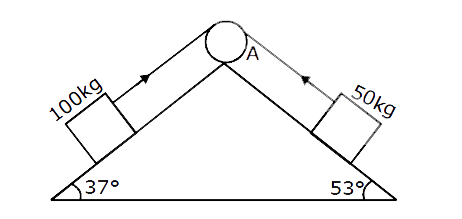
View SolutionTwo block of masses m1 and m2 are connected as shown in the figure. The acceleration of the block m2 is:

View Solution
