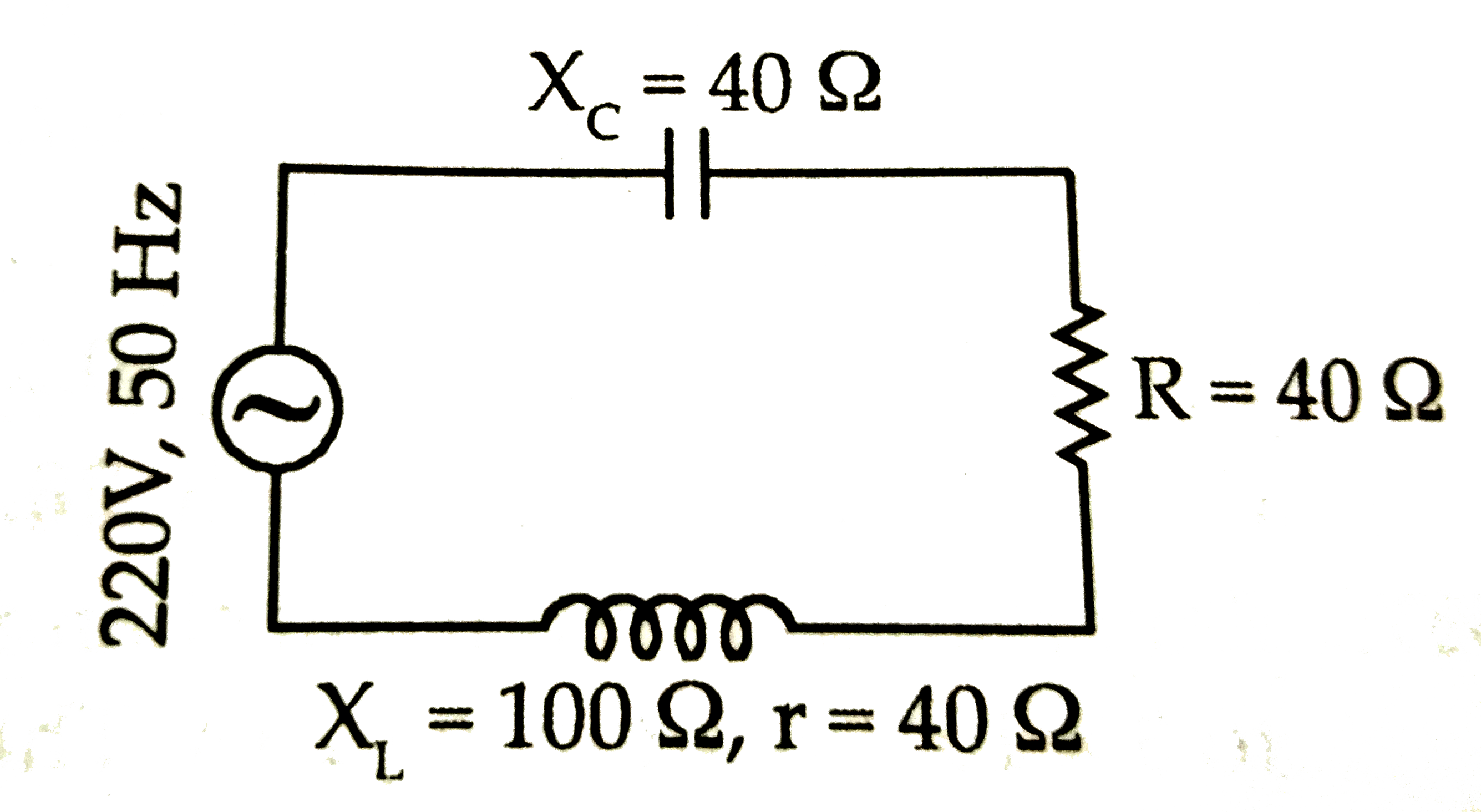
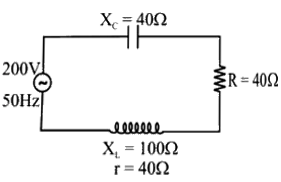
In an AC circuit, the reactannce is equal to the resistance. The power factor of the circuit will be
1
12
1√2
zero
The correct Answer is:C
To find the power factor of an AC circuit where the reactance (X) is equal to the resistance (R), we can follow these steps:
1. Understand the Power Factor:
The power factor (PF) of an AC circuit is defined as the cosine of the phase angle (φ) between the voltage and the current. Mathematically, it is given by:
Power Factor=cos(ϕ)
2. Relate Reactance and Resistance:
In the given circuit, we know that the reactance (X) is equal to the resistance (R). Therefore, we can express this relationship as:
X=R
3. Determine the Phase Angle:
The phase angle (φ) can be determined using the formula:
tan(ϕ)=XR
Since X=R, we can substitute to get:
tan(ϕ)=RR=1
4. Calculate the Phase Angle:
The angle whose tangent is 1 is:
ϕ=45∘
5. Calculate the Power Factor:
Now, we can find the power factor using the cosine of the phase angle:
Power Factor=cos(45∘)
The value of cos(45∘) is:
cos(45∘)=1√2
Final Answer:
Thus, the power factor of the circuit is:
Power Factor=1√2≈0.707
The power factor (PF) of an AC circuit is defined as the cosine of the phase angle (φ) between the voltage and the current. Mathematically, it is given by:
Power Factor=cos(ϕ)
In the given circuit, we know that the reactance (X) is equal to the resistance (R). Therefore, we can express this relationship as:
X=R
The phase angle (φ) can be determined using the formula:
tan(ϕ)=XR
Since X=R, we can substitute to get:
tan(ϕ)=RR=1
The angle whose tangent is 1 is:
ϕ=45∘
Now, we can find the power factor using the cosine of the phase angle:
Power Factor=cos(45∘)
The value of cos(45∘) is:
cos(45∘)=1√2
Thus, the power factor of the circuit is:
Power Factor=1√2≈0.707
Topper's Solved these Questions
Similar Questions
Knowledge Check
The power factor of a circuit is
AZ/RBR/ZCR/XDX/RPower factor of the circuit is –
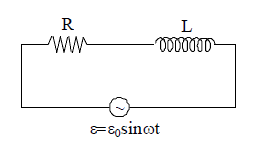 ARωLBR√R2+ω2L2CRR2+ω2L2Dnone of these
ARωLBR√R2+ω2L2CRR2+ω2L2Dnone of theseThe power factor of L-R circuit is-
AωLRBR√(ωL)2+R2CωLRD√ωLR