In a regular polygon of n sides, each corner is at a distance r from the centre. Identical charges are placed at (n−1) corners. At the centre, the intensity is E and the potential is V. The ratio V/E has magnitude
rn
r(n−1)
(n−1)/r
r(n−1)/n
The correct Answer is:B
Step by step video, text & image solution for In a regular polygon of n sides, each corner is at a distance r from the centre. Identical charges are placed at (n-1) corners. At the centre, the intensity is E and the potential is V. The ratio V//E has magnitude by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
In a regular polgyon of n sides, each cormer is at a distance r from the center . Identical chargs are placed at ( n-1) corners . At the center, the intensity is E and the potential is VM. The ratio V/E has magnitude .
ArnBr(n−1)C(n−1)/rDr(n−1)/nIn a regular polygon of n sides, each corner is at a distance r from the centre. Identical charges of magnitude Q are placed at (n−1) corners. The field at the centre is
AkQr2B(n−1)kQr2Cnn−1kQr2Dn−1nkQr2In a regular polygon of n sides, each corner is at a distance r from the centre. Identical charges each of magnitude q are placed at corners. The field at the centre is
Ann−1kqr2Bn−1nkqr2C0D(n−1)kqr2
The magnitude of electric intensity at a distance x from a charge q is E.An identical charge is placed at a distance 2x from it Then the magnitude of the force it experience is ..
View SolutionFour identical charges q are placed at the corners of a square of side a. Find the potential energy of one of the charges due to the remaining charges.
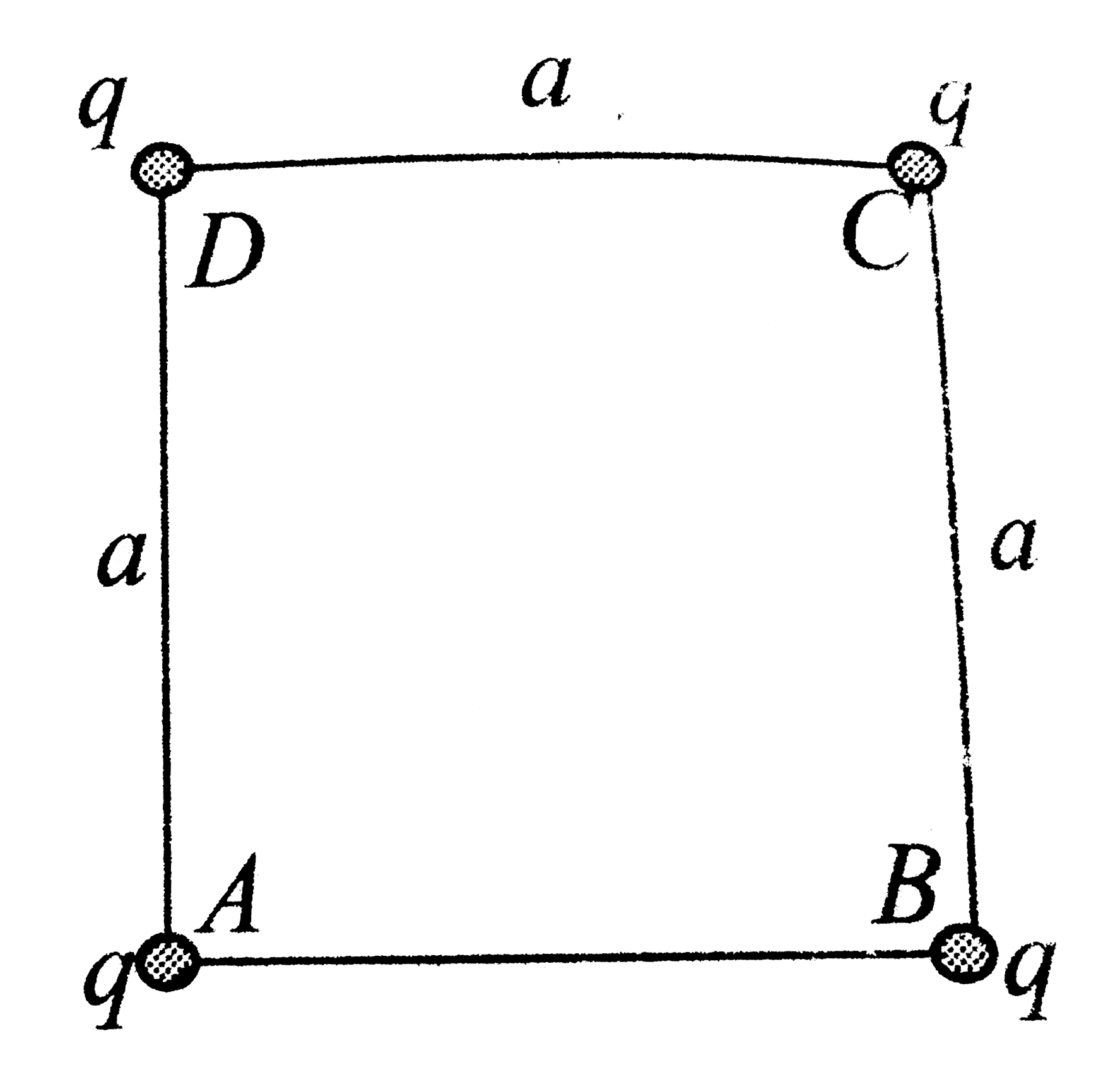 .
.
View SolutionFour point charges are placed at the corners of a square of side l. Calculate potential at the centre of square.
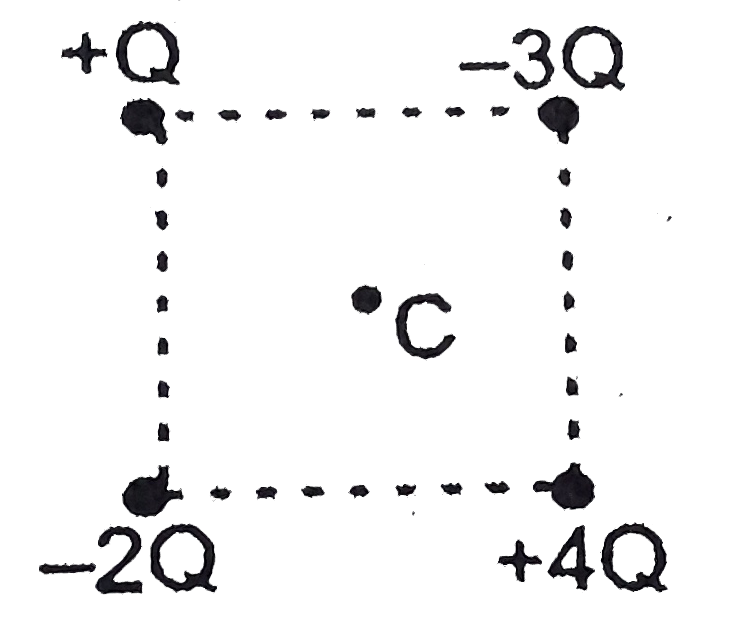
View SolutionAt each corner of an equilateral triangle identical charges are placed. Then at the centre of the triangle
View SolutionFour idential charges each of charge q are placed at the corners of a square .Then at the centre of the square the resultant electric intensity E and the net electric potential V are
View Solution
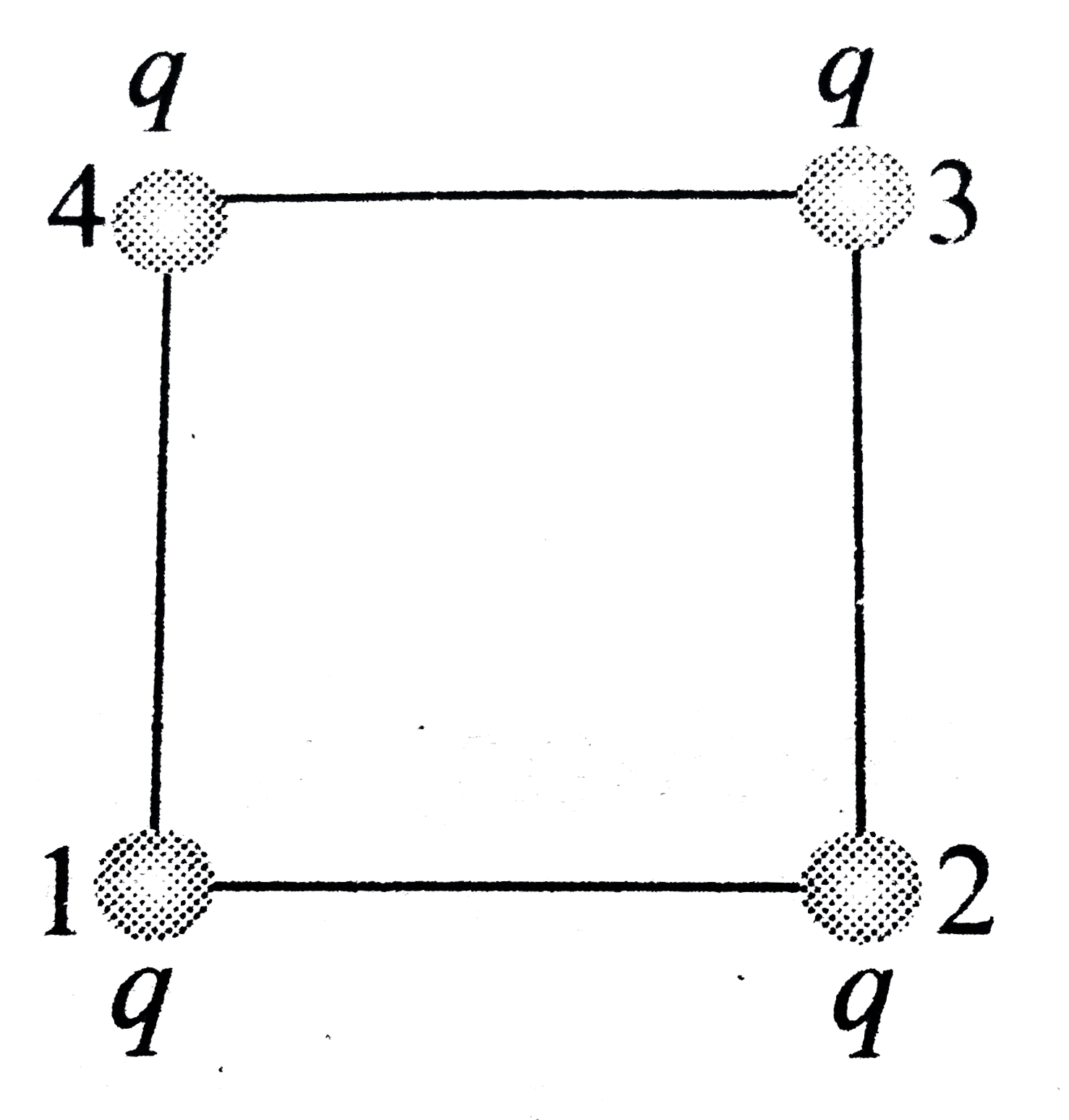 .
.