One moles of an ideal monoatomic gas undergo the state change as shown in following graph (ln 2 = 0.7)
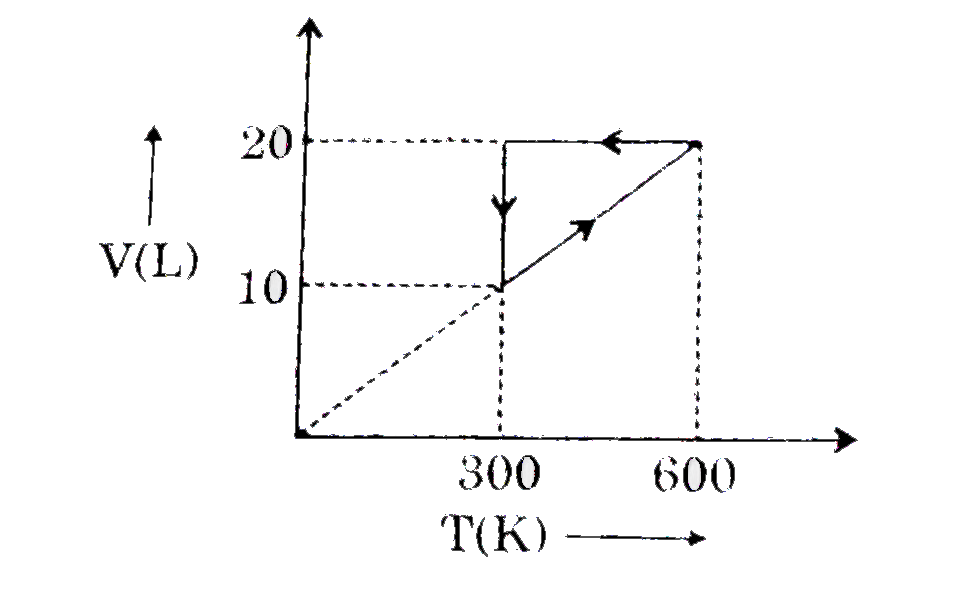
Efficiency of the cycle will be :
50%
25%
13.63%
12%
The correct Answer is:D
Topper's Solved these Questions
- GRAPHICAL INTERPRETATIONBook:GRB PUBLICATIONChapter:GRAPHICAL INTERPRETATIONExercise:Comprehension 2
Explore 1 Video
- GRAPHICAL INTERPRETATIONBook:GRB PUBLICATIONChapter:GRAPHICAL INTERPRETATIONExercise:Comprehension 3
Explore 1 Video
- GRAPHICAL INTERPRETATIONBook:GRB PUBLICATIONChapter:GRAPHICAL INTERPRETATIONExercise:Comprehension 1
Explore 1 Video
- F-BLOCK ELEMENTSBook:GRB PUBLICATIONChapter:F-BLOCK ELEMENTSExercise:Subjective type
Explore 7 Videos
- HYDROCARBON (ALIPHATIC)Book:GRB PUBLICATIONChapter:HYDROCARBON (ALIPHATIC)Exercise:Previous years jee questions
Explore 28 Videos
Similar Questions
Knowledge Check
One moles of an ideal monoatomic gas undergo the state change as shown in following graph (ln 2 = 0.7)
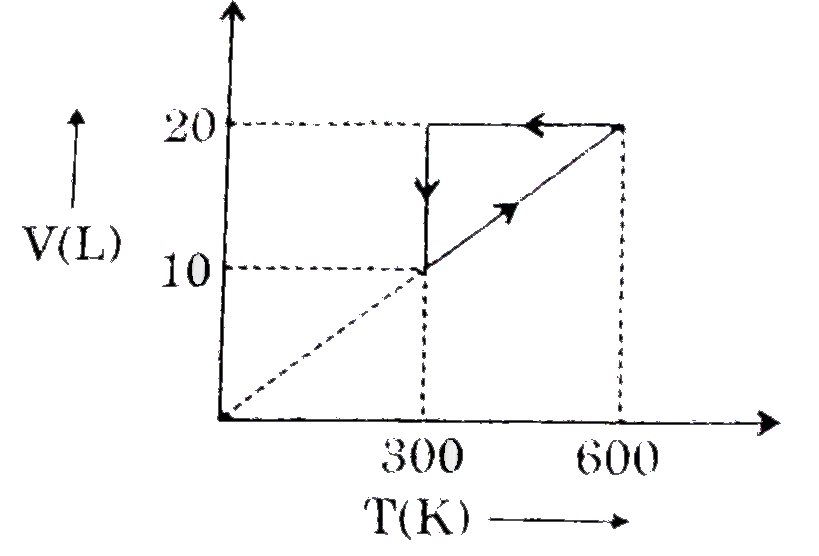
Correct graph for the process in paragraph is:A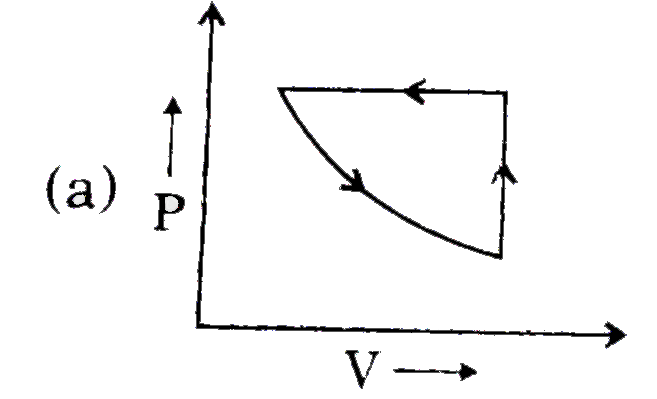 B
B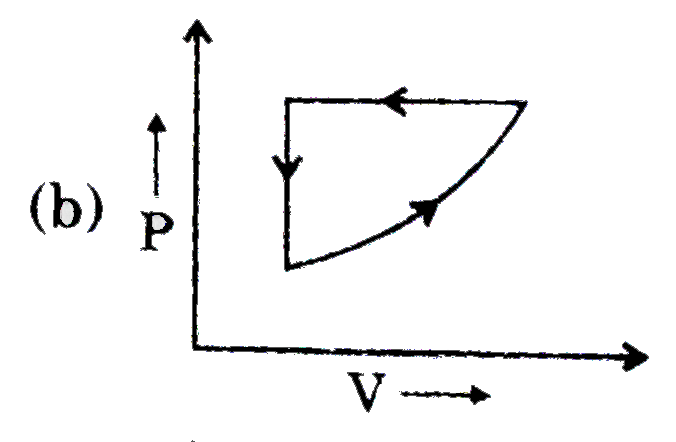 C
C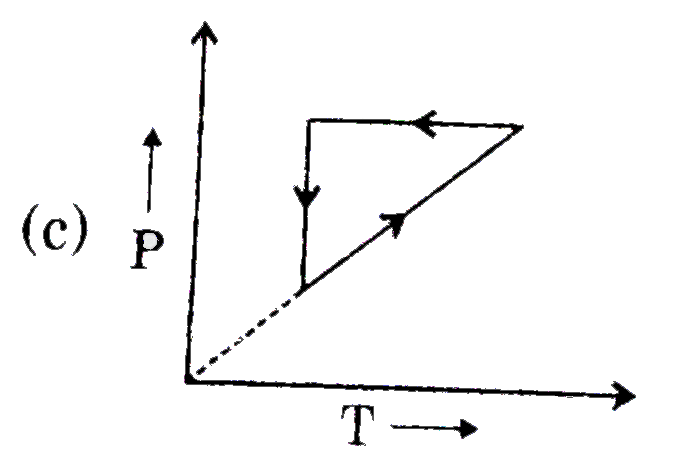 D
D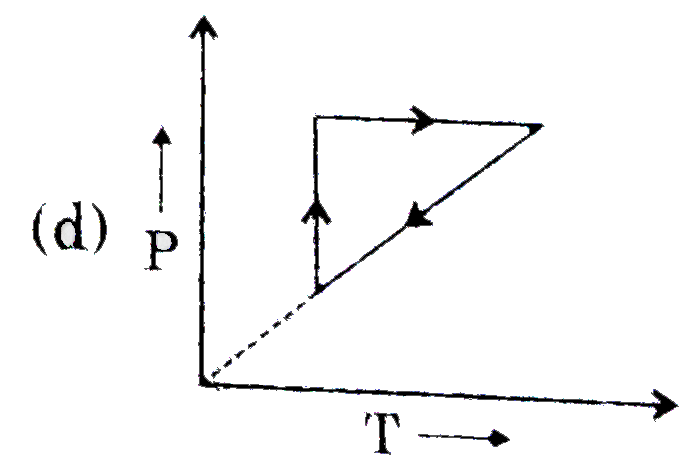
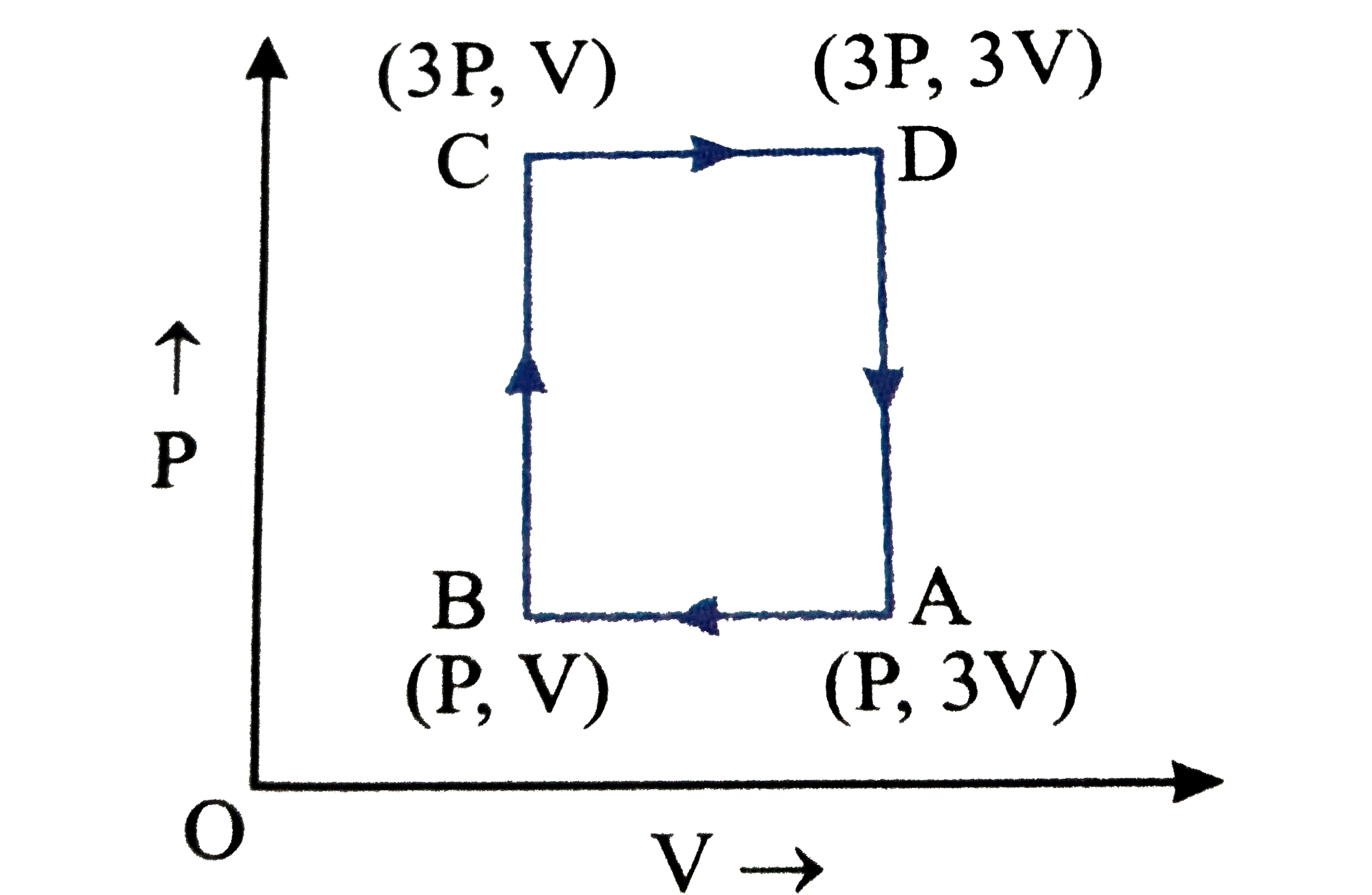
An ideal monoatomic gas is carried around the cycle ABCDA as shown in the figure. The efficiency of the gas cycle is
 A421B221C431D231
A421B221C431D231An ideal monoatomic gas is carried around the cycle ABCDA as shown in the figure. The efficiency of the cycle is ltBrgt
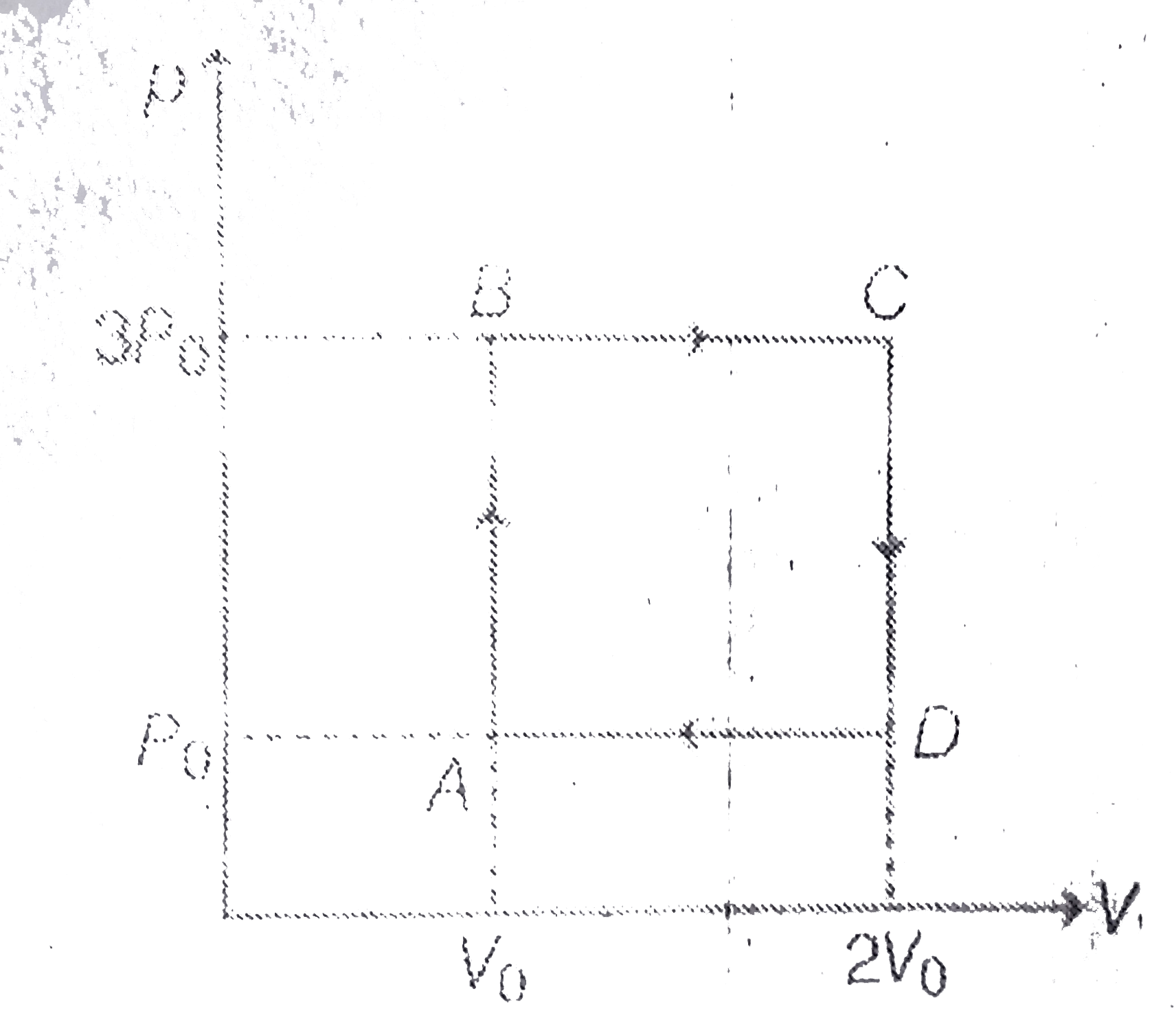 A28.6%B34.2%C46.8%D62.3%
A28.6%B34.2%C46.8%D62.3%
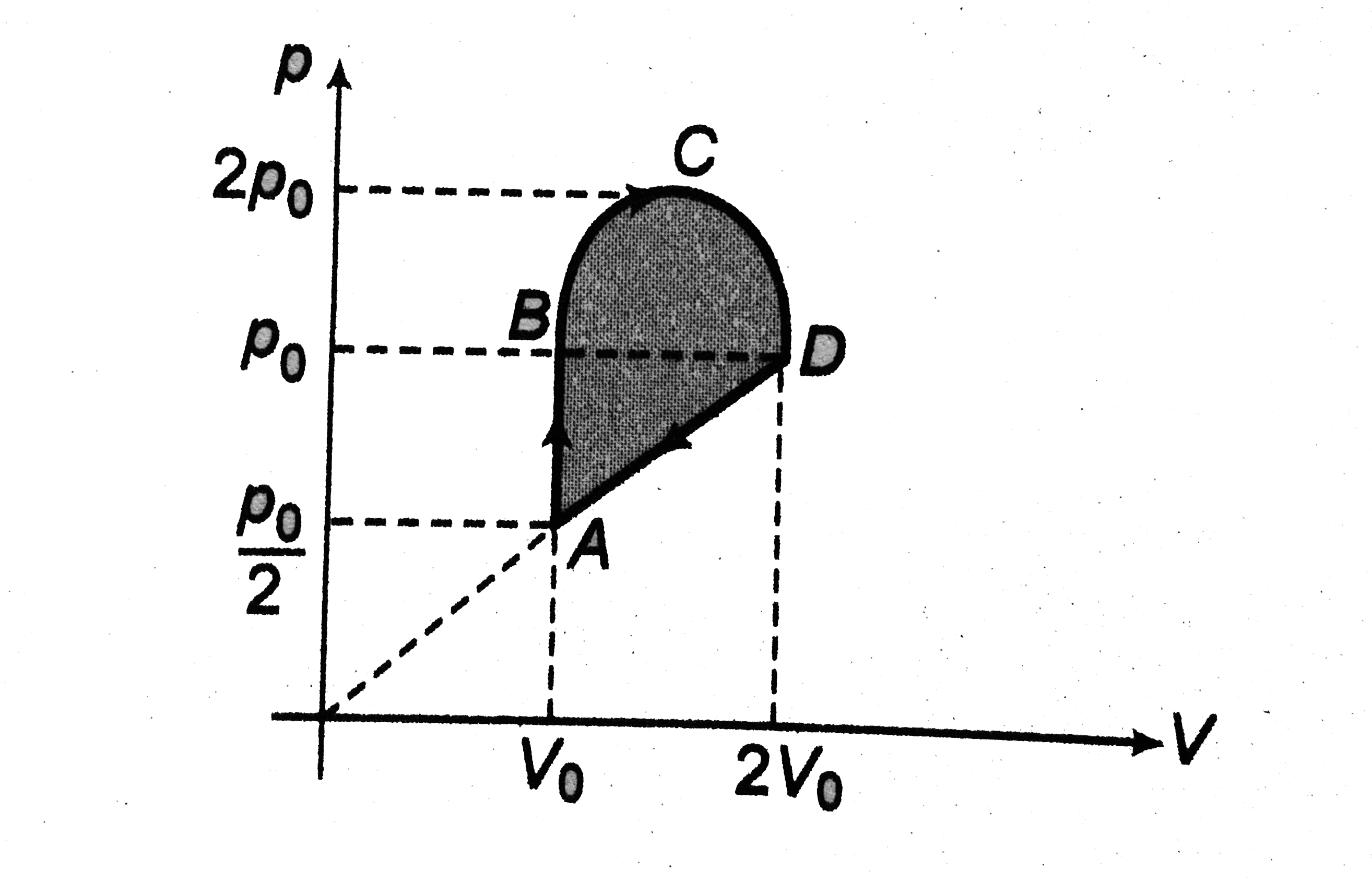
Two moles of a monatomic ideal gas undergo a cyclic process ABCDA as shown in figure. BCD is a semicircle. Find the efficiency of the cycle.
View SolutionAn ideal monoatomic gas is taken the cycle ABCDA as shown in following P−V diagram. The work done during the cycle is
View SolutionOne mole of an ideal monoatomic gas undergoes a process as shown in the figure. Find the molar specific heat of the gas in the process.
R is a gas constant.
View SolutionOne mole of an ideal monoatomic gas undergoes a cyclic process as shown in figure . Temperature at point 1 =300K and process 2−3 is isothermal .
_S01_115_O01.png)
The efficiency of cycle is
View SolutionOne mole of an ideal monoatomic gas undergoes a cyclic process as shown in figure. Then the change in the energy in expanding the gas from a to c along the path abc is:

View Solution

