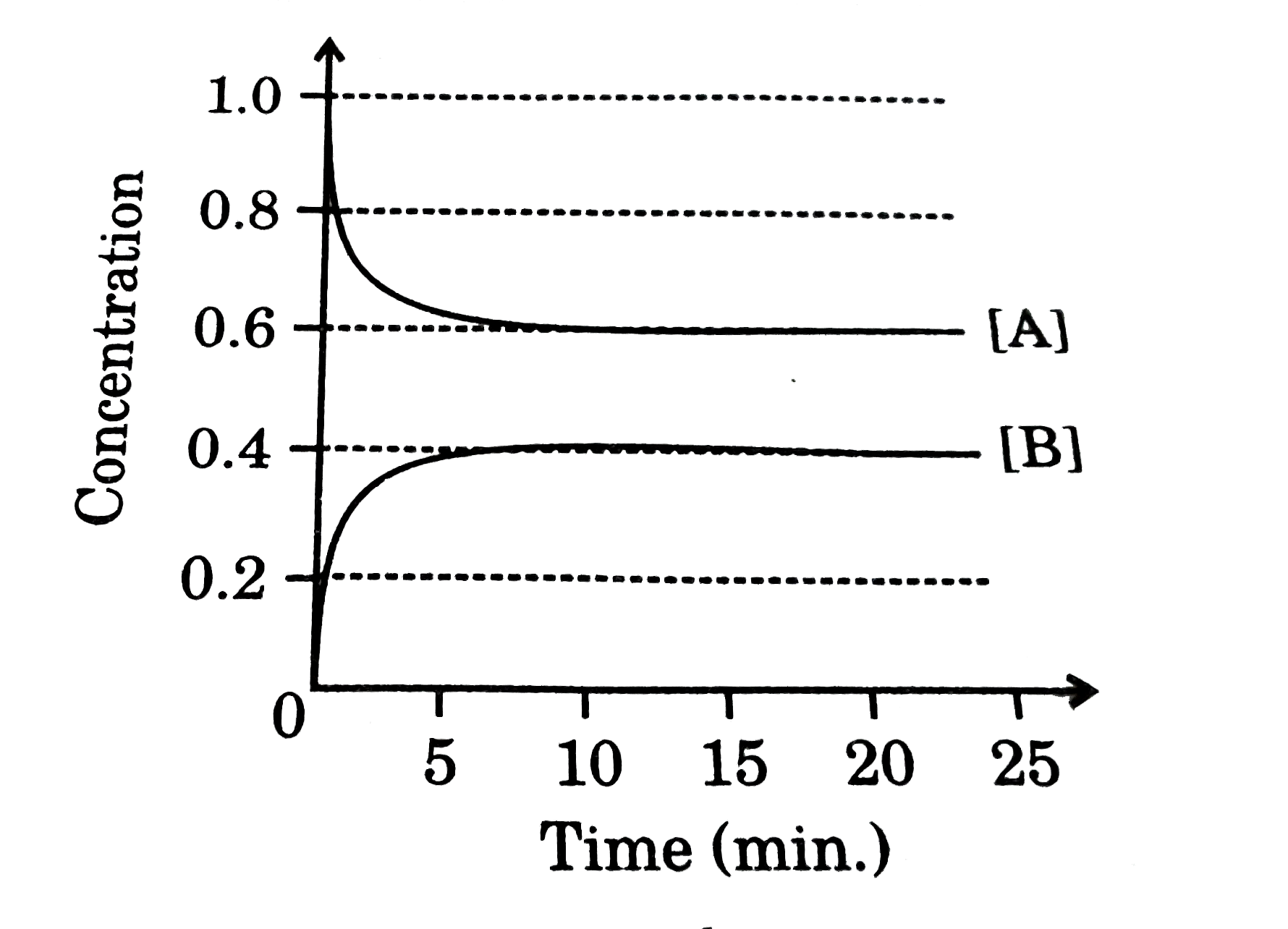
For the reversible reaction Akf⇐===⇒kbB (having Ist order in both direction) the concentration as a function of time are given for a certain experimantal run.
At what time (t) is the rete of change of concentration A equal to the rate of change of concentration of B in magnitude?
t=0only
t≥tequilibriumonly
t=0min only
At all times
The correct Answer is:D
Step by step video, text & image solution for For the reversible reaction A underset(k_(b))overset(k_(f))(hArr)B (having Ist order in both direction) the concentration as a function of time are given for a certain experimantal run. At what time (t) is the rete of change of concentration A equal to the rate of change of concentration of B in magnitude? by Chemistry experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- GRAPHICAL INTERPRETATIONBook:GRB PUBLICATIONChapter:GRAPHICAL INTERPRETATIONExercise:Comprehension 15
Explore 1 Video
- GRAPHICAL INTERPRETATIONBook:GRB PUBLICATIONChapter:GRAPHICAL INTERPRETATIONExercise:Comprehension 16
Explore 1 Video
- GRAPHICAL INTERPRETATIONBook:GRB PUBLICATIONChapter:GRAPHICAL INTERPRETATIONExercise:Comprehension 13
Explore 1 Video
- F-BLOCK ELEMENTSBook:GRB PUBLICATIONChapter:F-BLOCK ELEMENTSExercise:Subjective type
Explore 7 Videos
- HYDROCARBON (ALIPHATIC)Book:GRB PUBLICATIONChapter:HYDROCARBON (ALIPHATIC)Exercise:Previous years jee questions
Explore 28 Videos
Similar Questions
How many times will the rate of the reaction 2A+B→A2B change is the concentration is expressed in mol/mL ?
View SolutionThe reaction A+B→ products is first order in each of the reactants.
(a) How does the rate of reaction change if the concentration of A is increased by factor 3 ?
(b) What is the change in the rate of reaction if the concentration of A is halved and concentration of B is doubled ?
View Solution
Knowledge Check
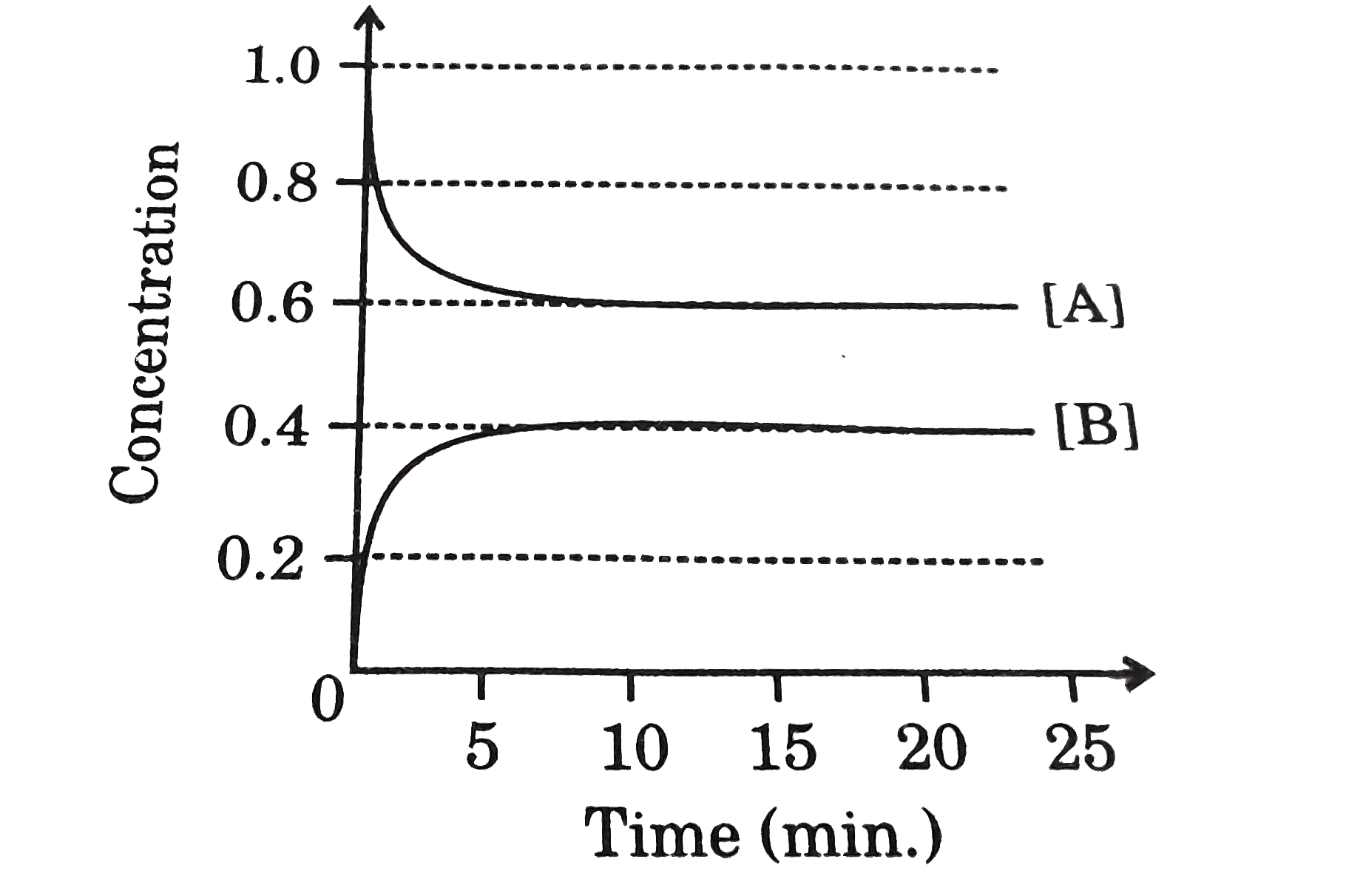
For the reversible reaction Akf⇐===⇒kbB (having Ist order in both direction) the concentration as a function of time are given for a certain experimantal run.
Calculate [B] at time t=15min.
[Given:kb=3min−1and1e=0.37]A0.37B0.153C0.2D0.252For the reaction AK1⇐===⇒K2B, if 'a' is the initial concentration of A and n is the number of moles of A reacting if initially no B was present then :
Adxdt=[K1(a−x)−K2x] initiallyBK1(a−xe)−K2xe=0 at equilibriumCK1+K2=K1.axeD(K1+K2)=1tln.xexe−xIn a first order reaction the concentration of product ’x’ at time 't' is given by the expression (a=initial concentration, k=rate constant, n=order)
Ax=a(1−e−kt)Bx=1a−xCx=12n−1Dx=aa−x
The concentrations of the reactant A in the reaction A →B at different times are given below:

The rate constant of the reaction according to the correct order of reaction is :
View SolutionIf the rate of reaction A→B triples on increasing the concentration of A by 9 times, then the order of reaction is
View SolutionFor the two step reaction in which both the steps are first order
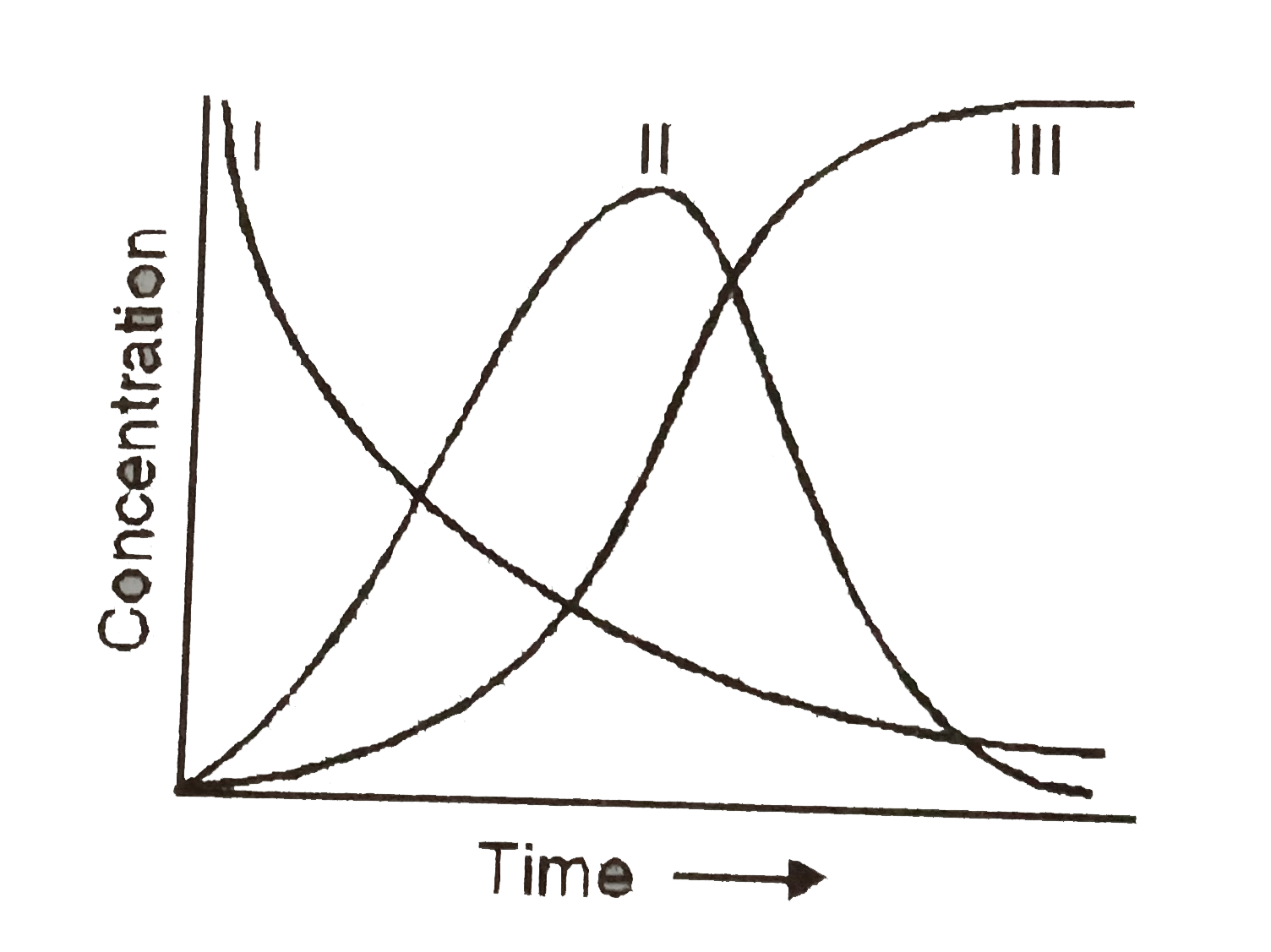
Rk1−−→I
Ik2−−→P
the rate of change of concentration of I is given by the plot
View SolutionConsider the reaction A→B. The concentration of both the reactants and the products varies exponentially with time. Which of the following figure correctly describes the change in concentration of reactants and products with time ?
View SolutionConsider the reaction A→B. The concentration of both the reactants and the products varies exponentially with time. Which of the following figure correctly describes the change in concentration of reactants and products with time ?
View Solution

