A body is simultaneously given two velocities, one 10ms−1 due east and other 20ms−1 due north-west. Calculate the resultant velocity.
The correct Answer is:14.74ms−1,16∘19' wast of north
To solve the problem of finding the resultant velocity of a body given two velocities, we will follow these steps:
Step 1: Understand the Directions
We have two velocities:
1. V1=10ms−1 due east.
2. V2=20ms−1 due north-west.
We will consider east as the positive x-direction and north as the positive y-direction. Therefore:
- East (V1) corresponds to the positive x-axis.
- North-West (V2) corresponds to a direction that is at a 45∘ angle from both the north and west axes.
Step 2: Break Down the North-West Velocity into Components
The north-west direction can be broken down into its x and y components using trigonometric functions:
- The x-component (west direction) will be negative since it is towards the west.
- The y-component (north direction) will be positive.
Using the angle 45∘:
- V2x=V2⋅cos(45∘)=20⋅1√2=20√2
- V2y=V2⋅sin(45∘)=20⋅1√2=20√2
Since the x-component is towards the west, we will take it as negative:
- V2x=−20√2
- V2y=20√2
Step 3: Combine the Components
Now we can combine the components of both velocities:
- Total x-component:
VRx=V1x+V2x=10+(−20√2)
- Total y-component:
VRy=V1y+V2y=0+20√2
Step 4: Calculate the Resultant Components
Calculating the x-component:
VRx=10−20√2=10−10√2(since 20√2=10√2)
Calculating the y-component:
VRy=20√2=10√2
Step 5: Calculate the Magnitude of the Resultant Velocity
The magnitude of the resultant velocity VR can be calculated using the Pythagorean theorem:
VR=√(VRx)2+(VRy)2
Substituting the values:
VR=√(10−10√2)2+(10√2)2
Step 6: Simplify the Expression
Calculating (10−10√2)2:
=100−200√2+200=300−200√2
Calculating (10√2)2:
=200
Thus,
VR=√(300−200√2)+200=√500−200√2
Step 7: Calculate the Direction of the Resultant Velocity
To find the angle α that the resultant makes with the north direction, we can use the tangent function:
tan(α)=VRyVRx=10√210−10√2
This will give us the angle in relation to the north direction.
Final Result
After calculating the above expressions, we can find the magnitude and direction of the resultant velocity.
We have two velocities:
1. V1=10ms−1 due east.
2. V2=20ms−1 due north-west.
- East (V1) corresponds to the positive x-axis.
- North-West (V2) corresponds to a direction that is at a 45∘ angle from both the north and west axes.
The north-west direction can be broken down into its x and y components using trigonometric functions:
- The x-component (west direction) will be negative since it is towards the west.
- The y-component (north direction) will be positive.
- V2x=V2⋅cos(45∘)=20⋅1√2=20√2
- V2y=V2⋅sin(45∘)=20⋅1√2=20√2
- V2x=−20√2
- V2y=20√2
Now we can combine the components of both velocities:
- Total x-component:
VRx=V1x+V2x=10+(−20√2)
- Total y-component:
VRy=V1y+V2y=0+20√2
Calculating the x-component:
VRx=10−20√2=10−10√2(since 20√2=10√2)
VRy=20√2=10√2
The magnitude of the resultant velocity VR can be calculated using the Pythagorean theorem:
VR=√(VRx)2+(VRy)2
Substituting the values:
VR=√(10−10√2)2+(10√2)2
Calculating (10−10√2)2:
=100−200√2+200=300−200√2
Calculating (10√2)2:
=200
Thus,
VR=√(300−200√2)+200=√500−200√2
To find the angle α that the resultant makes with the north direction, we can use the tangent function:
tan(α)=VRyVRx=10√210−10√2
This will give us the angle in relation to the north direction.
After calculating the above expressions, we can find the magnitude and direction of the resultant velocity.
Topper's Solved these Questions
Similar Questions
Knowledge Check
Two particles are thrown simultaneously from points A and B with velocities u1=2ms−1andu2−14ms−1, respectively, as shown in figure.
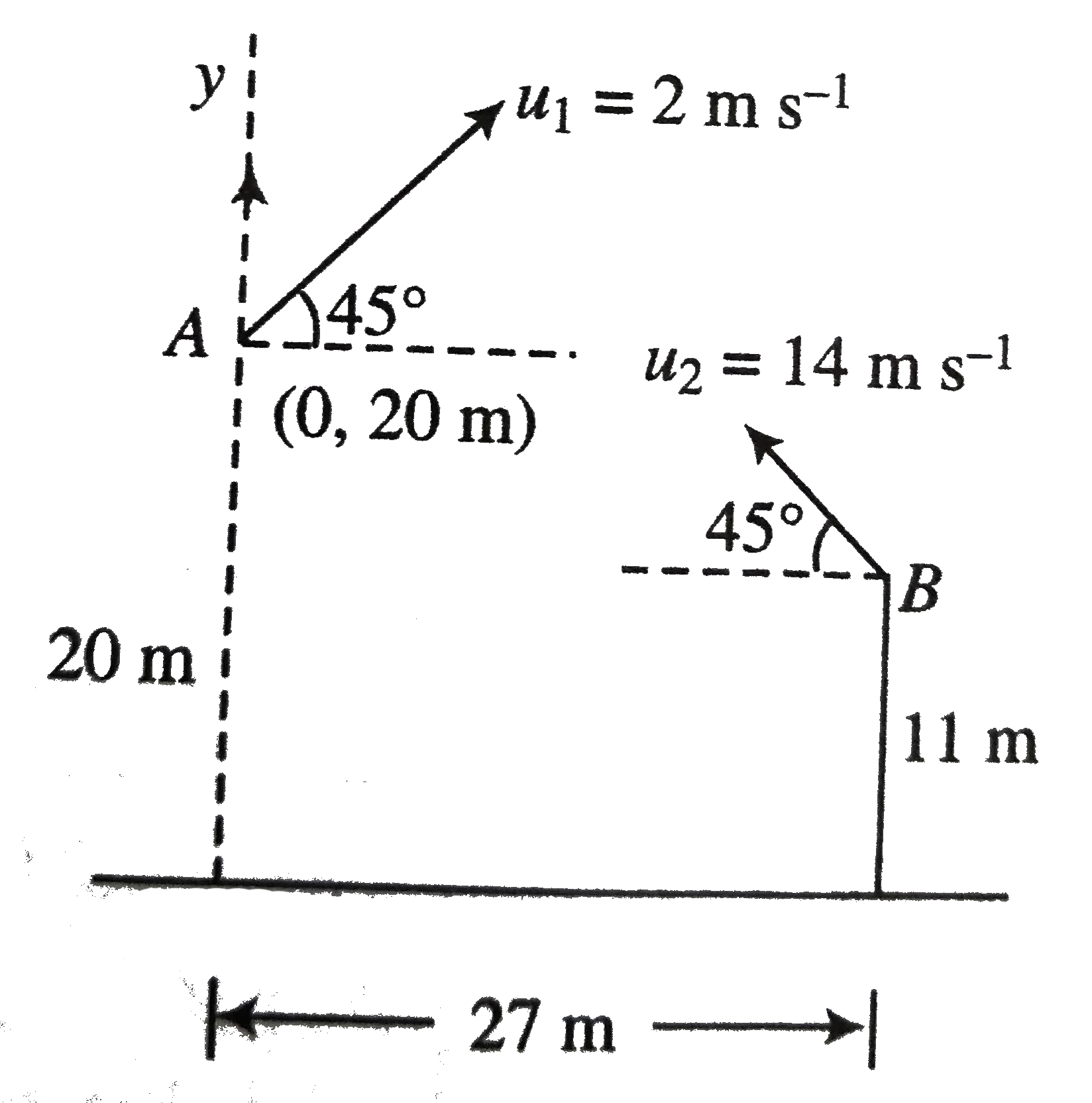
The relative velocity of B as seen from A inA−8√2ˆi+6(√2)ˆjB4√2ˆi+3(√3)ˆjC3√5ˆi+2(√3)ˆjD3√2ˆi+4(√3)ˆj
Caculate the resultant of two forces, one 12 N due east and other 9N due north .
View SolutionThe velocity of particle P due east is 4ms−1 and that of Q is 3ms−1 due north. What is the relative velocity of P w.r.t. Q.
View SolutionFind the resultant of two forces, one 6N due east and other 8N due north.
View SolutionFour forces are acting on a particle simultaneously : 50N due east , 40 N due north , 30 N due west and 20 N due south . Calculate the resultant force on the particle .
View SolutionA train is moving with a velocity of 30kmh−1 due East and a car is moving with a veloicty of 40kmh−1 due North . What is the velocity of car as appears to a passenger in the train ?
View SolutionA boy is moving westward with a velocity of 10ms−1. In 20 seconds , velocity changes to 5ms−1 southwards . Calculate the average acceleration of the boy in this interval
View SolutionTwo simultaneous forces are applied on a body , one 5N due east and other 7N due north . Find the result force on the body .
View Solution

