The point masses of 0.3 kg, 0.2 kg and 0.1 kg are placed at the corner of a right angles ΔABC, as shown in Fig. 8.49. find the moment of inertia of the system (i) about an axis through A and perpendicular to the plane of the diagram and (ii) about an axis along BC.
The correct Answer is:(i) 0.043kgm2 (ii) 0.027kgm2
To find the moment of inertia of the system about the specified axes, we will follow these steps:
Given Data:
- Mass at A (0.3 kg)
- Mass at B (0.2 kg)
- Mass at C (0.1 kg)
- Length of AB = 0.3 m
- Length of AC = 0.5 m
(i) Moment of Inertia about an Axis through A and Perpendicular to the Plane
1. Identify the distances from the axis:
- For mass at B (0.2 kg), the distance from A (point A to point B) is AB = 0.3 m.
- For mass at C (0.1 kg), the distance from A (point A to point C) is AC = 0.5 m.
2. Use the formula for moment of inertia:
The moment of inertia I about point A is given by:
IA=mB⋅d2B+mC⋅d2C
where mB and mC are the masses at B and C, and dB and dC are their respective distances from A.
3. Substitute the values:
IA=(0.2kg)⋅(0.3m)2+(0.1kg)⋅(0.5m)2
IA=(0.2)⋅(0.09)+(0.1)⋅(0.25)
IA=0.018kg m2+0.025kg m2
IA=0.043kg m2
(ii) Moment of Inertia about an Axis along BC
1. Identify the distances from the axis along BC:
- For mass at A (0.3 kg), the distance from BC is the perpendicular distance from A to line BC. Since BC is horizontal, we can use the height from A to BC, which is equal to AC = 0.5 m.
2. Use the formula for moment of inertia:
The moment of inertia IBC about the axis along BC is given by:
IBC=mA⋅d2A+mB⋅d2B
where mA and mB are the masses at A and B, and dA is the distance from A to BC, and dB is the distance from B to BC (which is 0 since B is on the line).
3. Substitute the values:
IBC=(0.3kg)⋅(0.5m)2+(0.2kg)⋅(0m)2
IBC=(0.3)⋅(0.25)+(0.2)⋅(0)
IBC=0.075kg m2+0
IBC=0.075kg m2
Final Answers:
- Moment of inertia about an axis through A and perpendicular to the plane: IA=0.043kg m2
- Moment of inertia about an axis along BC: IBC=0.075kg m2
- Mass at A (0.3 kg)
- Mass at B (0.2 kg)
- Mass at C (0.1 kg)
- Length of AB = 0.3 m
- Length of AC = 0.5 m
- For mass at B (0.2 kg), the distance from A (point A to point B) is AB = 0.3 m.
- For mass at C (0.1 kg), the distance from A (point A to point C) is AC = 0.5 m.
The moment of inertia I about point A is given by:
IA=mB⋅d2B+mC⋅d2C
where mB and mC are the masses at B and C, and dB and dC are their respective distances from A.
IA=(0.2kg)⋅(0.3m)2+(0.1kg)⋅(0.5m)2
IA=(0.2)⋅(0.09)+(0.1)⋅(0.25)
IA=0.018kg m2+0.025kg m2
IA=0.043kg m2
- For mass at A (0.3 kg), the distance from BC is the perpendicular distance from A to line BC. Since BC is horizontal, we can use the height from A to BC, which is equal to AC = 0.5 m.
The moment of inertia IBC about the axis along BC is given by:
IBC=mA⋅d2A+mB⋅d2B
where mA and mB are the masses at A and B, and dA is the distance from A to BC, and dB is the distance from B to BC (which is 0 since B is on the line).
IBC=(0.3kg)⋅(0.5m)2+(0.2kg)⋅(0m)2
IBC=(0.3)⋅(0.25)+(0.2)⋅(0)
IBC=0.075kg m2+0
IBC=0.075kg m2
- Moment of inertia about an axis through A and perpendicular to the plane: IA=0.043kg m2
- Moment of inertia about an axis along BC: IBC=0.075kg m2
Topper's Solved these Questions
- ROTATIONAL MOTIONBook:SL ARORAChapter:ROTATIONAL MOTIONExercise:Problem
Explore 24 Videos
- PROPERTIES OF SOLIDSBook:SL ARORAChapter:PROPERTIES OF SOLIDSExercise:All Questions
Explore 97 Videos
- System of particles & rotational MotionBook:SL ARORAChapter:System of particles & rotational MotionExercise:EXERCISE
Explore 353 Videos
Similar Questions
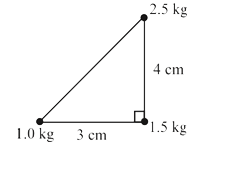
Three point particles of masses 1.0 kg, 1.5 kg and 2.5 kg are placed at three corners of a right angle triangle as shown in figure. The centre of mass of the system is at a point :
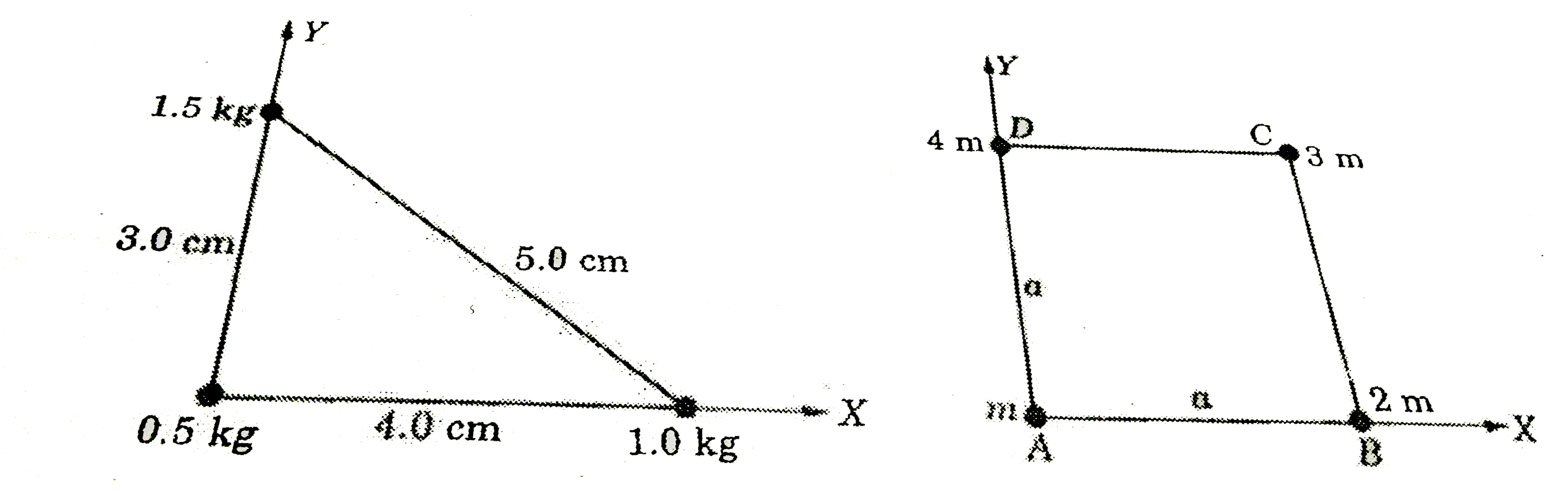
View SolutionThree particles of masses 0.50 kg, 1.0 kg and are placed at the corners of a right angle triangle, as shown in fig. Locate the centre of mass of the system.
View Solution
Knowledge Check
In the figure shown ABCD is a lamina of mass 12kg. The moment of inertia of the given body about an axis passing through D, and perpendicular to the plane of the body is
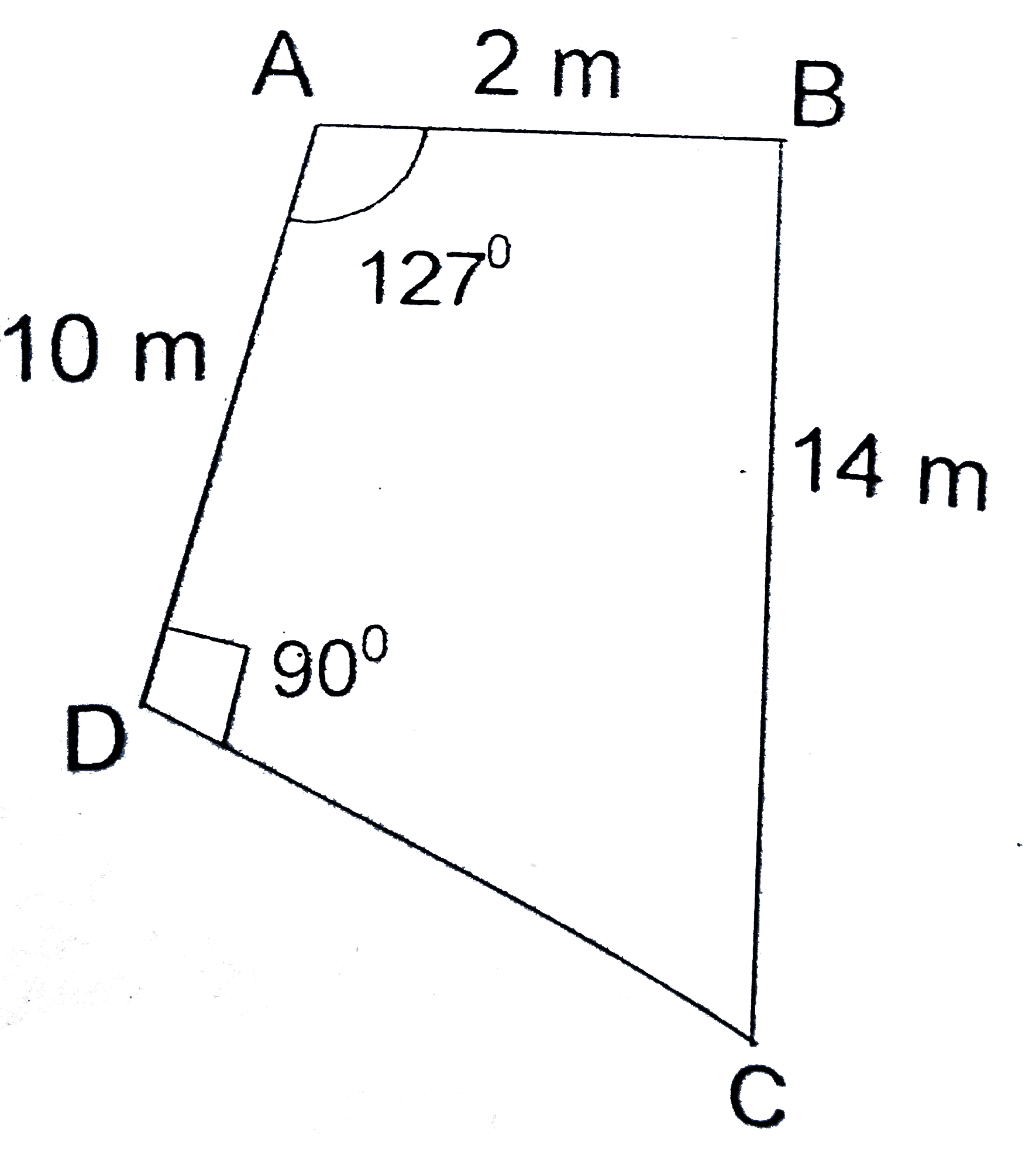 A256kgm2B512kgm2C200kgm2D100kgm2
A256kgm2B512kgm2C200kgm2D100kgm2Four point masses, each of value m, are placed at the corners of a square ABCD of side 1. The moment of inertia of this system about an axis through A and parallel to BD is
Aml2B2ml2C√3ml2D3ml2Three identical masses, each of mass 1kg, are placed at the corners of an equilateral triangle of side l. Then the moment of inertia of this system about an axis along one side of the triangle is
A3l2Bl2C34l2D32l2
Four point masses of 20 g each are placed at the corners of a square ABCD of side 5 cm, as shown in Fig. 8.48. find the moment of inertia of the system (i) about an axis coinciding with the side BC and (ii) about an axis through A and perpendicular to the plane of the square.

View SolutionParticle of masses 2 kg, 2 kg, 1 kg and 1 kg are placed at the corners A, B, C, D of a square of side L as shown in Fig. Find the centre of mass of the system.

View SolutionFind the moment of inertia of a disk about an axis passing through a point on its circumference perpendicular to its plane.
View SolutionTwo masses of 3 kg and 5 kg are placed at 30 cm and 70 cm marks respectively on a light wooden meter scale, as shown in Fig. 8.51. what will the moment of inertia of the system about an axis through (i) 0 cm mark and (ii) 100 cm mark, and perpendicular to the meter scale?

View SolutionThe diameter of a thin circular disc of mass 2 kg is 0.2 m. Its moment of inertia about an axis passing through the edge and perpendicular to the plane of the disc is
View Solution

