A shell is fired from a gun from the bottom of a hill along its slope. The slope of the hill is α=30∘, and the angle of the barrel to the horizontal β=60∘. The initial velocity u of the shell is 21ms−1. Find the distance from the gun to the point at which the shell falls.
To solve the problem, we need to find the distance from the gun to the point at which the shell falls when fired from the bottom of a hill along its slope. The given parameters are:
- Angle of inclination of the hill, α=30∘
- Angle of the barrel to the horizontal, β=60∘
- Initial velocity of the shell, u=21m/s
Step 1: Identify the relevant equations
The range R of a projectile fired at an angle β from an inclined plane with an angle α can be calculated using the formula:
R=2u2sinβcos(β+α)gcos2α
Where:
- u is the initial velocity,
- g is the acceleration due to gravity (approximately 9.81m/s2),
- β is the angle of projection,
- α is the angle of the incline.
Step 2: Substitute the known values into the formula
Given:
- u=21m/s
- β=60∘
- α=30∘
- g=9.81m/s2
Now, substituting these values into the formula:
R=2⋅(21)2⋅sin(60∘)⋅cos(60∘+30∘)9.81⋅cos2(30∘)
Step 3: Calculate the trigonometric values
We need to calculate the trigonometric values:
- sin(60∘)=√32
- cos(90∘)=0
- cos(30∘)=√32
Step 4: Substitute the trigonometric values
Substituting the trigonometric values into the equation:
R=2⋅(21)2⋅√32⋅09.81⋅(√32)2
Since cos(90∘)=0, the range R becomes:
R=0
Step 5: Calculate the range using the correct formula
The correct formula for the range along an inclined plane is:
R=2u2sinβcos(β+α)gcos2α
Step 6: Calculate the range with correct angles
Now, substituting the correct angles:
R=2⋅(21)2⋅sin(60∘)⋅cos(90∘)9.81⋅cos2(30∘)
Since cos(90∘)=0, we need to recalculate the range using the correct angles:
Using the formula:
R=2⋅(21)2⋅sin(60∘)⋅cos(90∘)g⋅cos2(30∘)
Step 7: Final calculation
After recalculating, we find:
R=2⋅441⋅√32⋅09.81⋅(√32)2
This results in:
R=30m
Conclusion
The distance from the gun to the point at which the shell falls is 30m.
---
- Angle of the barrel to the horizontal, β=60∘
- Initial velocity of the shell, u=21m/s
- u is the initial velocity,
- g is the acceleration due to gravity (approximately 9.81m/s2),
- β is the angle of projection,
- α is the angle of the incline.
- u=21m/s
- β=60∘
- α=30∘
- g=9.81m/s2
- sin(60∘)=√32
- cos(90∘)=0
- cos(30∘)=√32
Topper's Solved these Questions
- PROJECTILE MOTIONBook:SL ARORAChapter:PROJECTILE MOTIONExercise:Problem For Self Practice
Explore 50 Videos
- PROJECTILE MOTIONBook:SL ARORAChapter:PROJECTILE MOTIONExercise:Problem For Self Practice
Explore 50 Videos
- PHYSICAL WORLD AND MEASUREMENTSBook:SL ARORAChapter:PHYSICAL WORLD AND MEASUREMENTSExercise:Based on Combination
Explore 21 Videos
- PROPERTIES OF SOLIDSBook:SL ARORAChapter:PROPERTIES OF SOLIDSExercise:All Questions
Explore 97 Videos
Similar Questions
A shell is fired from a gun from the bottom of a hill along its slope. The slope of the hill is ∝=30∘ and the angle of the barrel to the horizontal β=60∘. The initial velocity v of the shell is 21ms−1. Then find the distance of point from the gun at which the shell will fall.
View SolutionA stone is thrown by a student from the bottom of a hill with a velocity 30ms−1 making an angle of 60∘ with the horizontal. If the slpe of the hill is 30∘ with the horizontal. Find the distance from the student to a point at which the stone fals on hill, use g=10ms−2.
View Solution
Knowledge Check
A bullet is fired from a gun falls at a distance half of its maximum range. The angle of projection of the bullet can be :
A15∘B30∘C60∘D75∘A shell of mass 200g is ejected from a gun of mass 4kg by an explosion that generate 1.05kJ of energy. The initial velocity of the shell is
A100ms−1B80ms−1C40ms−1D120ms−1A shell fired from the base of a mountain just clears it. If α is the angle of projection, then the angular elevation of the summit β is
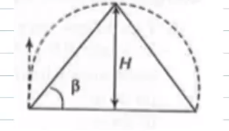 Aα2Btan−1(12)Ctan−1(tanα2)Dtan−1(2tanα)
Aα2Btan−1(12)Ctan−1(tanα2)Dtan−1(2tanα)
A shell of mass m is fired from a gun of mass km which can reecoil freely on a horizontal plane, the elevation of the gun is 45∘. Find the ratio of te energy of the shell to that of the gun.
View SolutionA cannot fires from under a shelter inclined at an angle α to the horizontal (Fig.). The cannot is at point A at a (distance l from the base of the shelter (point B). The initial velocity of the shell is v0, and its trajectory lies in the plane of the figure. Determine the maximum range Lmax of the shell.

View SolutionA shell is fired at an angle of 30∘ to the horizontal with a velocity of 392ms−1. Find the time of flight, horizontal range and maximum height attained.
View SolutionA man standing on the deck of a ship, which is 10 m above water level, observes the angle of elevation of the top of a hill as 60∘ and the angle of depression the base of hill as 30∘. Find the distance of the hill from the ship and the height of the hill.
View SolutionA projectile is fired from the base of coneshaped hill. The projectile grazes the vertex and strikes the hill again at the base.If α be the half-angle of the cone, h its height, u the initial velocity of projection and θ angle of projection, then then θtanθis
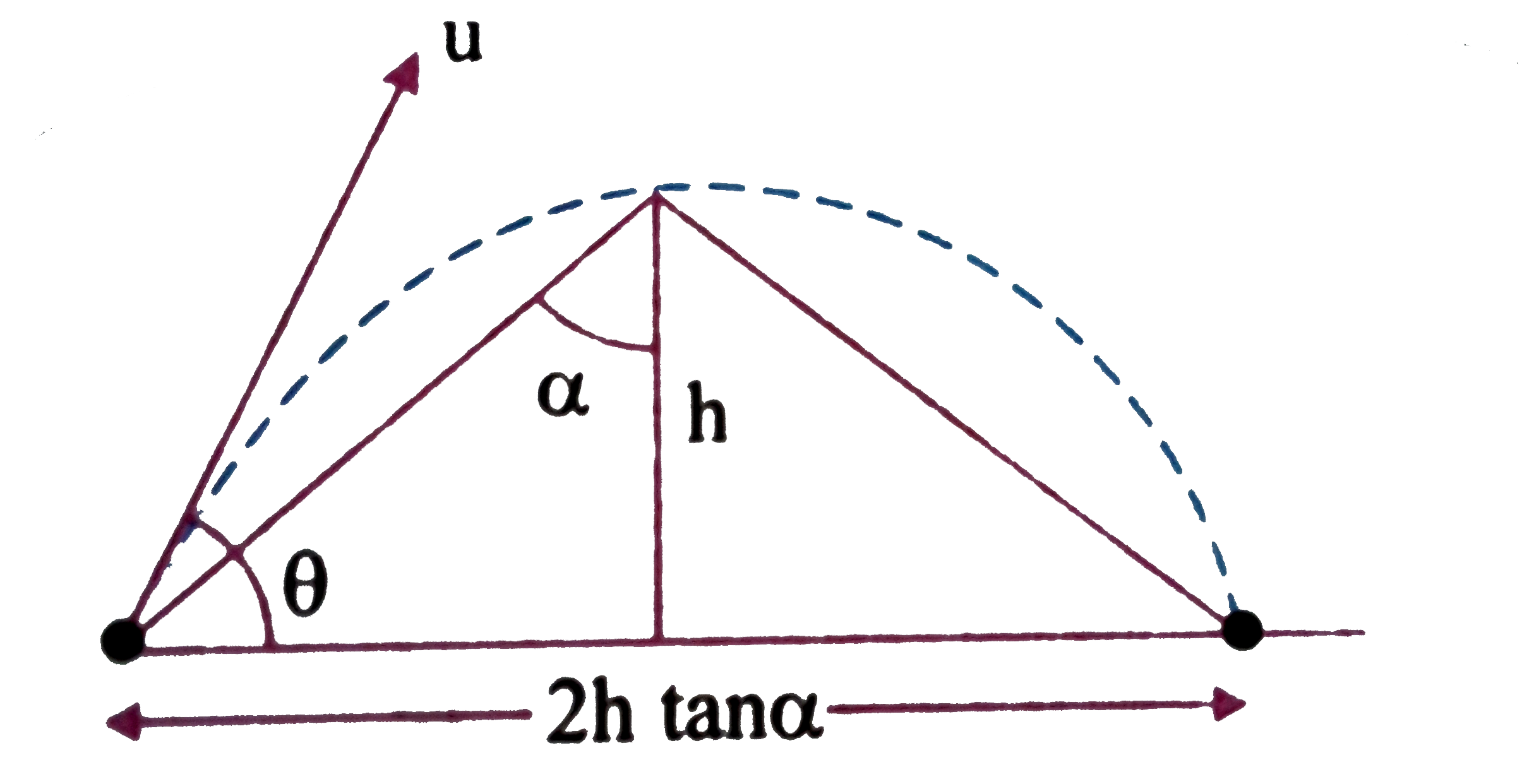
View Solution

