A particle is attached by a light string of length 3 a to a fixed point and describes a horizontal circle of radius a with uniform angular velocity ω If, when the particle is moving in this manner, is suddenly stopped and then let go,find its velocity when the string is vertical in its subsequent motion :
[2ga(3−2√2)]1/2
2ga(3−2√2)
ga(3−2√2)
2ga3−2√2
The correct Answer is:A
Step by step video, text & image solution for A particle is attached by a light string of length 3 a to a fixed point and describes a horizontal circle of radius a with uniform angular velocity omega If, when the particle is moving in this manner, is suddenly stopped and then let go,find its velocity when the string is vertical in its subsequent motion : by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- RIGID BODIES AND ROTATIONAL MOTIONBook:PHYSICS GALAXY - ASHISH ARORAChapter:RIGID BODIES AND ROTATIONAL MOTIONExercise:paragraph
Explore 24 Videos
- RIGID BODIES AND ROTATIONAL MOTIONBook:PHYSICS GALAXY - ASHISH ARORAChapter:RIGID BODIES AND ROTATIONAL MOTIONExercise:MCQ
Explore 16 Videos
- RIGID BODIES AND ROTATIONAL MOTIONBook:PHYSICS GALAXY - ASHISH ARORAChapter:RIGID BODIES AND ROTATIONAL MOTIONExercise:Conceptual MCQs Single Option Correct
Explore 39 Videos
- NEWTONS LAWS OF MOTIONBook:PHYSICS GALAXY - ASHISH ARORAChapter:NEWTONS LAWS OF MOTIONExercise:Unsolved Numerical Problem
Explore 81 Videos
- WORK, ENERGY AND POWERBook:PHYSICS GALAXY - ASHISH ARORAChapter:WORK, ENERGY AND POWERExercise:unsolved
Explore 1 Video
Similar Questions
A particle of mass 21 g attached to a string of 70cm length Keeping the string always taut the ball describes a horizontal circle of radius 15cm Calculate the angular speed of the ball .
View SolutionA particle is attached by means of two equal strings to two points A and B in the same vertical line and describes a horizontal circle with a uniform angular speed. If the angular speed of the particle is 2√2g/h with AB=h, show that the ratio of the tensions of the strings is 5:3
View Solution
Knowledge Check
A particle moving along a circule path of radius 'r' with uniform angular velocity ω. Its angular acceleration is
Arω2Br/ωCzeroDω/rA particle P is attached by means of two equal strings to two points A and B is same vertical line and describes horizontal circle with uniform angular speed 2√2gh where AB = h
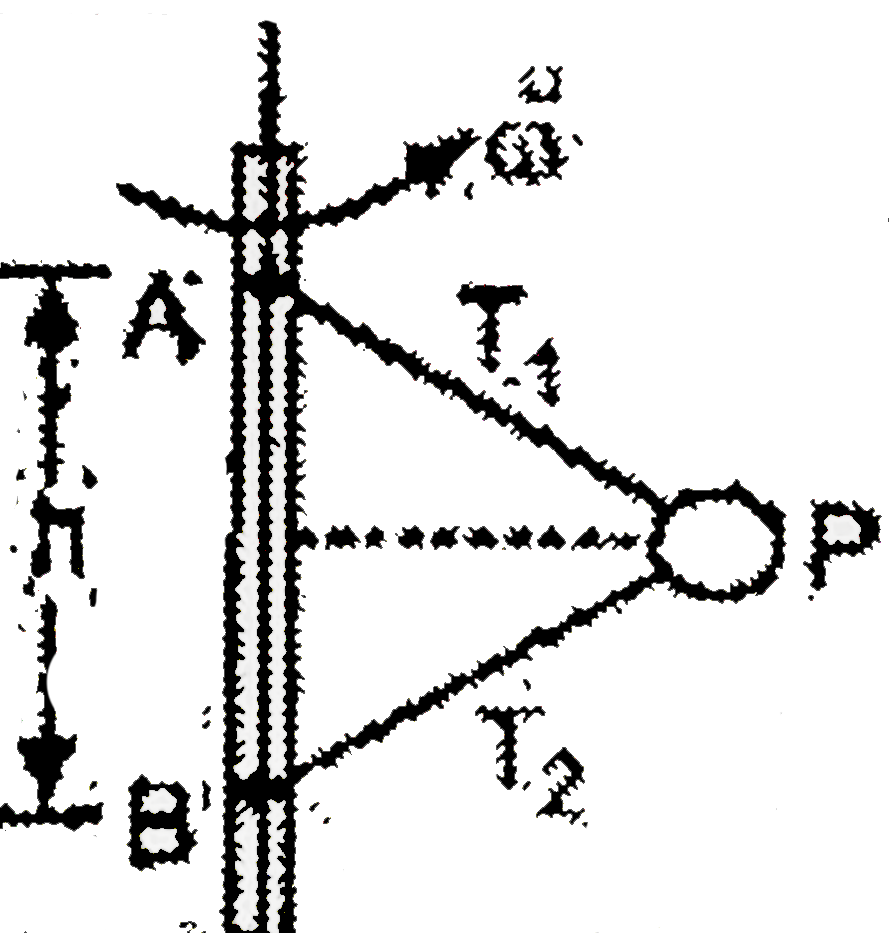 AT1>T2BT1:T2=5:3CT1:T2=√5:√3DT1=T2
AT1>T2BT1:T2=5:3CT1:T2=√5:√3DT1=T2A particle of maas m is attched to a light string of length l, the other end of which is fixed. Initially the string is kept horizontal and the particle is given an upwrd velocity v. The particle is just able to complete a circle
AThe string becomes slack when the partice reaches its highest pointBThe velocity of the particle becomes zero at the highest point.CThe kinetic energy of the ball in initial position was 12mv2=mgDThe particle again passes through the initial position.
A particle, held by a string whose other end is attached to a fixed point C, moves in a circle on a horizontal frictionless surface. If the string is cut, the angular momentum of the particle about the point C
View SolutionA particle of mass 21 g attached to a string of 70 cm length is whirled round in a horizontal circle. If the period of revolution is 2s, find the tension in the string.
View SolutionA stone is tied to one end of a steing and rotated in horizontal circle with a uniform angular velocity. The tension in the string is T, if the lrngth of the string is halved and its angular velocity is doubled , the tension in the string will be
View SolutionA particle of mass M is moving in a horizontal circle of radius R with uniform speed V. When it moves from one point to a diametrically opposite point , its
View SolutionA particle of mass M is moving in a horizontal circle of radius R with uniform speed V. When it moves from one point to a diametrically opposite point, its
View Solution

